Общие методы программирования решения дифференциальных уравнений

Министерство образования РФ

Сибирский государственный технологический университет

Факультет автоматизации и информационных технологий

Кафедра автоматизации производственных процессов

Лабораторные работы

	Разработал: студ. гр. 24-2 __________ Захаров А.С.        (подпись) _________________________                                     (дата) Принял: __________ Устимец В.А.        (подпись) _________________________                              (дата, оценка)

 

Общие методы программирования решения дифференциальных уравнений

Исследованию подлежит дифф. уравнение вида .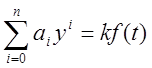

- порядок производной;

- -ая производная от искомой переменной;

-возмущение действующее на систему;

- коэффициенты уравнения.

Уравнение описывает поведение объекта под действием возмущающего воздействия.

Правая часть – возмущение, левая часть – сам объект.

Имеется 2 алгоритма решения повысительный и понизительный. Учитывая что повысительный алгоритм имеет не высокую помехозащищённость – им пользоваться не будем. При понизительном алгоритме(метод понижения порядка производной) уравнение разрешается относительно высшей производной и приобретает вид:

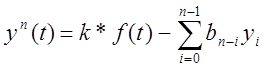, где .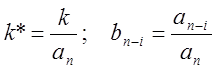

Анализируя левую часть уравнения можно предложить следующую схему её решения: принимать что значение функции левой части нам известно, тогда последовательным интегрированием получим все производные низших порядков в плоть до получения в итоге искомой переменной . На модели данную операцию можно представить в виде цепочки модулей интеграторов, количество которых равно порядку решаемого дифф. уравнения.

                           

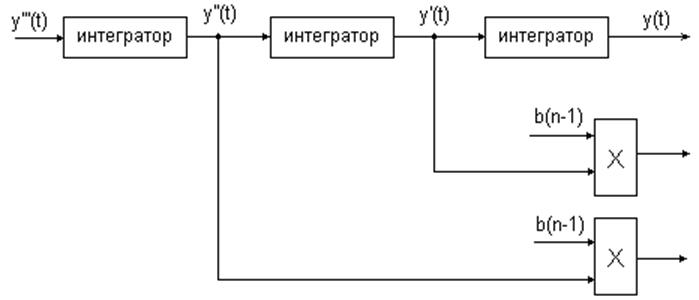
Обратим ся к правой части уравнения , отметим что она равна n-ой производной , т.е. можно утверждать что выполнив операции(математ.) правой части уравнения мы получим значение функции .

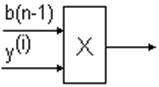
На модели данную операцию можно представить в виде модуля сумматора на вход которого поступают 2 слагаемых, 1-ое слагаемое равное возмущению действующему на систему, на модели она может быть представлена в виде спец. модуля – источника возмущения : второе слагаемое равно сумме включающую произведение искомой переменной и её производных достепени включительно, на коэффициенты дифф. уравнения разрешённого относительно старшей производной. На модели составляющая второго слагаемое могут быть представлены модулями  умножителями, на вход каждого из которых будут поступать значение коэффициента  и значение производной .

Рассмотренный алгоритм схему с кольцевой структурой , которая после установки начальных условий и её возбуждениявозмущением  работает как единое целоевыдовая на выходе искомую функцию  которая и подлежит дальнейшему исследованию.

Исследование графической модели

Задание

Набрать решение дифференциального уравнения:

y”(t) + a₁y’(t) + a₀y(t) = f(t).

В качестве исходных значений для исследования принять:

коэффициент а₀=10;

коэффициент а₁=1;

начальные условия y’(0) = 0;

y(0) = 1;

возмущения действующие на объект :

f(t) = 2Sin80t;

период моделирования 0 – 20 с.

Провести исследование системы при различных значениях параметров.

Решение поставленной задачи

  Для решения поставленной задачи будем использовать метод понижения порядка производной. Разработка в несколько этапов:

1.  Этап – разрешим уравнение относительно старшей производной

y”(t) = f(t) - a₁y’(t) - a₀y(t).

Полученое уравнение представляет собой структурную схему в которой каждый элемент математической операции соответствует определённое звено.

2. Этап – средствами SIMULINK соберём блок схему решения левой части последнего уравнения которая должна формировать сигнал производной и выходной переиенной. Представим её в виде цепочки из 2x интеграторов, поскольку данная задача требует рашения с начальными условиями выбираем настройку интеграторовна внешние начальные условия.

Блок – схема решения данного уравнения

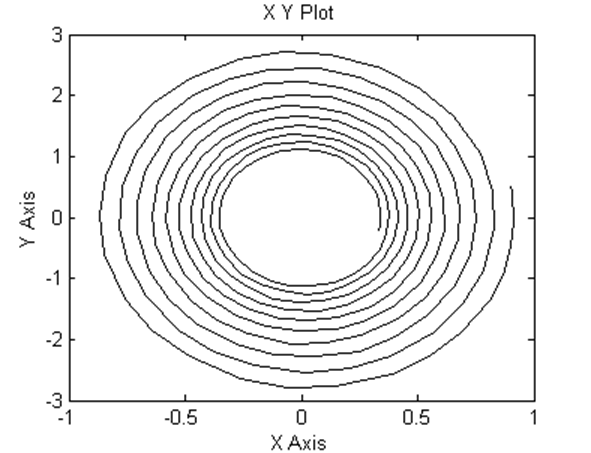
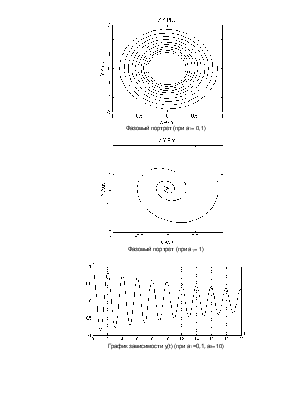
Фазовый портрет (при а₁= 0,1)

Фазовый портрет (при а­₁= 1)

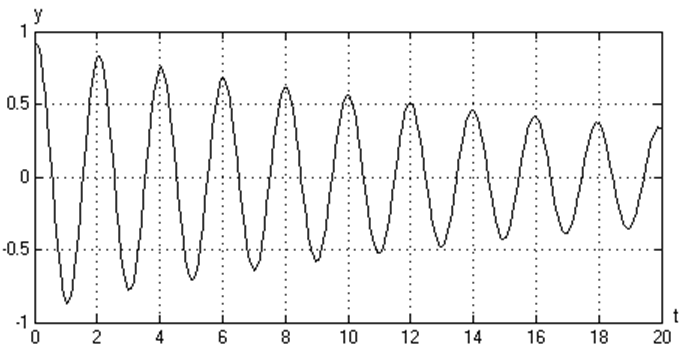
График зависимости y(t) (при а₁=0,1, а₀=10)

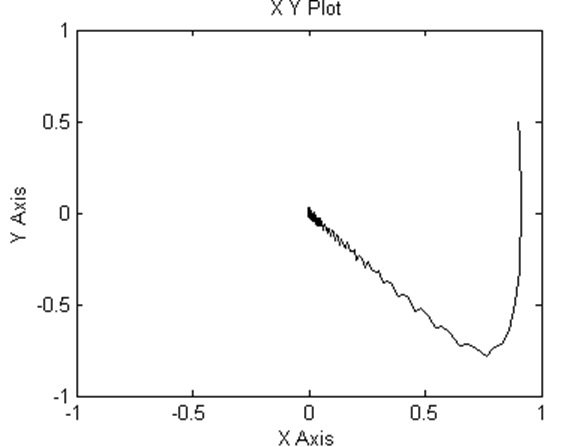
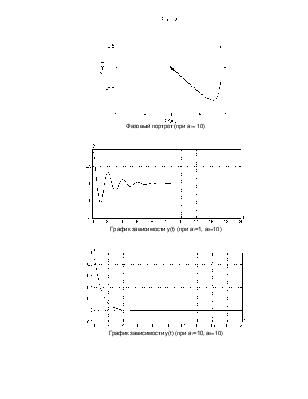
Фазовый портрет (при а­₁= 10)

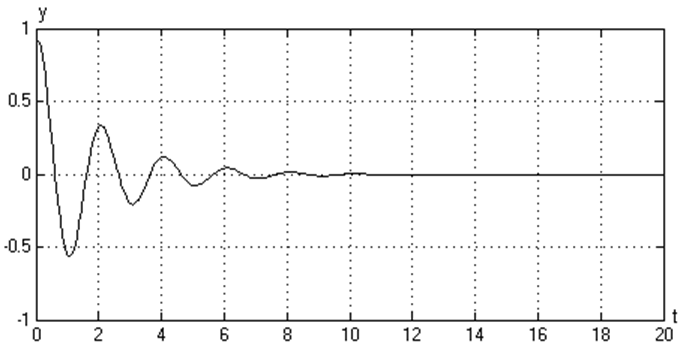
График зависимости y(t) (при а₁=1, а₀=10)

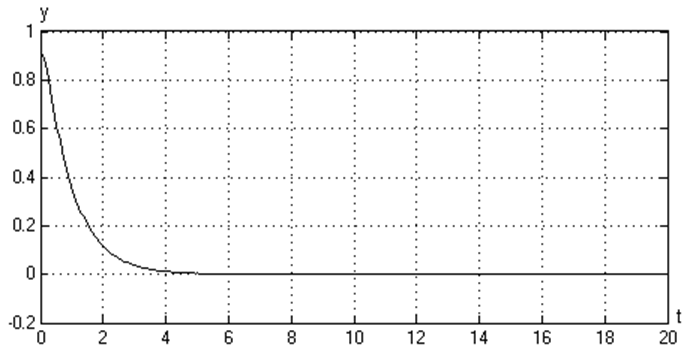
График зависимости y(t) (при а₁=10, а₀=10)

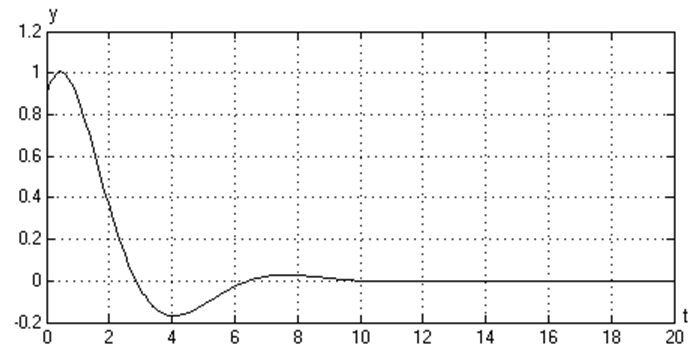
График зависимости y(t) (при а₁=1, а₀=1)

Модель одноемкостного объекта

Рассматриваются три типовых объекта, которые могут являться объектами регулирования в различных технологических цепочках химического производства: термостат (рисунок 1); емкость, приток и отток которой происходит самотеком (рисунок 2); емкость, приток которой происходит самотеком, а отток при помощи насоса (рисунок 3).

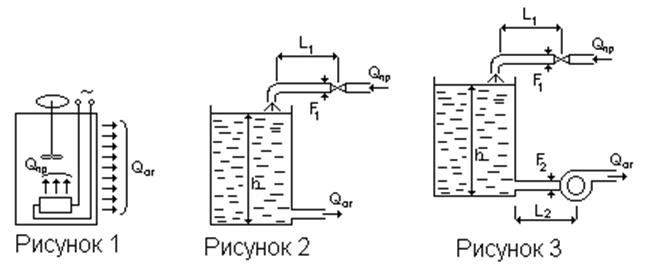
Рисунок 1 – Термостат

Рисунок 2 – Емкость, приток и отток которой происходит самотеком

Рисунок 3 – Емкость, приток которой происходит самотеком, а отток при помощи насоса

Модель А и Б

Модель объекта будем составлять как модель объекта регулирования. При этом в качестве регулируемого параметра в первом случае будет температура жидкости в емкости, а во втором и третьем – уровень жидкости в баке h.

Рассмотрим 1 случая, при котором в качестве регулируемого параметра выступает температура жидкости в емкости.

Запишем уравнение баланса:

.                                                    (1)

В случае нарушения баланса часть энергии соберется в емкости. Уравнение баланса примет вид:

,                                                (2)

где Q_пр – приток тепла, ккал/с;

       Q_от – отток тепла, ккал/с;

       Q(t) – температура, ^оС;

       С – теплоемкость среды в объекте, ккал/град.

Принимая, что отток тепла зависит от температуры и, полагая эту зависимость линейной, получим:                             .                                                                 (3)

где r - коэффициент самовыравнивания, ккал/град.

Смысл названия коэффициента самовыравнивания состоит в том, что в случае если этот коэффициент больше нуля, от объект сам, без внешнего воздействия всегда приходит к некоторому установившемуся состоянию, причем, тем быстрее и тем с меньшей статической ошибкой, чем больше этот коэффициент.

Подставляя уравнение (3) в уравнение (2), получим дифференциальное уравнение, описывающее поведение объекта:

.                                                (4)

Преобразуем полученное уравнение к виду:

.                                          (5)

Обозначив С/r через Т_о, 1/r через К получим выражение:

,                                               (6)

где Т_о – постоянная времени объекта;

      К – коэффициент усиления объекта.

Принимая обобщенные обозначения Q(t)=y и Q_пр(t)=х, запишем:

.                                                   (7)

Как видно, моделью одноемкостного объекта может служить дифференциальное уравнение первого порядка.

Нахождение дифференциального уравнения реального объекта

Определяющими переменными для дифференциального уравнения являются величины T_o, K и x(t).

Постоянную времени технологического объекта можно принимать как отношение объема аппарата (V, м³) к скорости движения рабочей среды через аппарат (v, м/с).

Степень самовыравнивания определяю двумя путами: из анализа физических характеристик процесса или на основании опытных данных. В последнем случае степень самовыравнивания определяют по величине коэффициента передачи объекта:

,

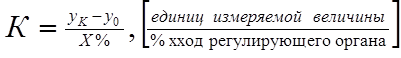где у_К – конечное значение, которое приобретает измеряемая величина при возмущающем воздействии Х.

Моделирование объекта в Matlab

Создадим 2 примера реализации данной модели в Matlab.

Пример 1

Разрешим уравнение (7) относительно старшей производной:

.

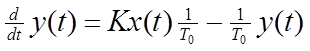Полученное уравнение в Matlab можно изобразить в виде:

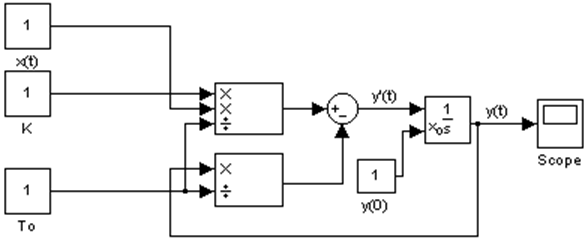
Рисунок 4 – Модель одноемкостного объекта

Пример 2

Запишем передаточную функцию данного объекта:

.

Полученное уравнение в Matlab можно изобразить в виде:

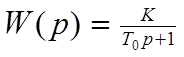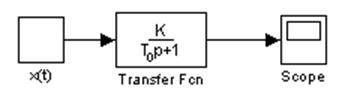Рисунок 5 – Модель одноемкостного объекта