Проверка параметрических гипотез для парных выборок с помощью персонального компьютера, страница 2

  Несмещенная оценка для показателя асимметрии Ан = -0.71206;

  Несмещенная оценка для показателя эксцесса Ен = 60092.15681;

  СКО показателя асимметрии Sa = 0.51210;

  СКО показателя эксцесса Se = 1.06266.

  Гипотеза о нормальности распределения по критерию формы принимается.

  Интервальная оценка:

  Нижняя граница доверительного интервала = -30.53824;

  Верхняя граница доверительного интервала = 5.73824;

  Доверительный интервал при заданной вероятности = 36.27648.

2. Проверка гипотезы об однородности двух дисперсий

Наглядным примером для использования гипотезы об однородности может служить задача о сравнительной оценке точности двух способов или средств измерений. Имеется две выборки объёмом n_X  и  n_Y  по которым найдены выборочные дисперсии  и . Проверяется гипотеза о том, что две выборки взяты из одной генеральной совокупности, а различие между ними обусловлено влиянием случайных ошибок, т.е. незначимо.

Для проверки гипотезы используется распределение Фишера и статистический критерий следующего вида:

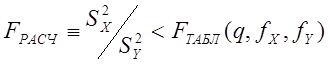,                                           (1)

где ,  - числа степеней свободы, с учётом которых по таблице находят граничные значения критической статистики F при заданном уровне значимости q (в данной работе q = 0,01).

Если неравенство (1) не выполняется, то различие между дисперсиями значимо, т.е. они неоднородны.

Результаты расчётов для проведения проверки данной гипотезы

Находим значения выборочных дисперсий  и :

,          .

Рассчитываем статистический F - критерий Фишера:

.

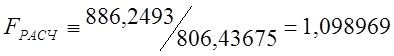Находим табличное значение F – критерия Фишера [1]:

F_ТАБЛ (q, f_X, f_Y) = 3.00,

где f_X  - число степеней свободы большей дисперсии,  f_Х = 19;

      f_Y  - число степеней свободы меньшей дисперсии,  f_Y = 19;

      q – заданный уровень значимости, q = 0,01.

Так как условие (1) выполняется , следовательно, гипотеза об однородности двух дисперсий  и  принимается, т.е. они однородны.

3. Проверка гипотезы об однородности средних двух выборок

Проверка данной гипотезы позволяет установить, вызвано ли расхождение между средними случайными ошибками измерения или связано с определёнными закономерностями, т.е. значимо. Эта процедура используется в тех случаях, когда необходимо установить идентичность параметров объектов, находящихся в одних условиях. Проверка осуществляется с применением t – статистики Стьюдента. Пусть имеется две выборки объёмом n_X  и  n_Y , тогда  и - соответствующие средние арифметические значения, а  и  - выборочные дисперсии. Возможны два случая:

1. В случае однородности дисперсий  и  гипотеза принимается по следующему неравенству:

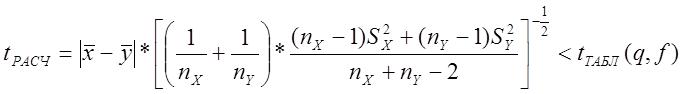,             (2)

где ,  - табличное значение распределения Стьюдента.

2. В случае неоднородности дисперсий  и  гипотеза принимается с помощью следующего неравенства:

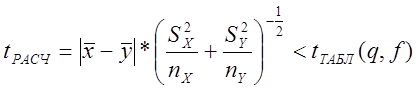,                                      (3)

где 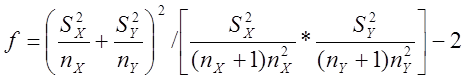 - число степеней свободы, округляется до целого значения.

Если неравенство (2) или (3) не выполняется, то расхождение между средними случайными  и  значимо, следовательно, гипотеза не принимается.

Результаты расчётов для проведения проверки данной гипотезы

Рассчитываем t – критерий Стьюдента для случая при однородности дисперсий  и :

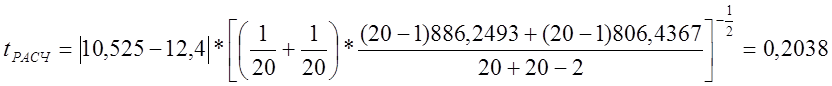
Находим табличное значение t – критерия Стьюдента [1] при q = 0,01  и  f = 38:

.

Так как , следовательно, расхождение между средними случайными  и  не значимо, т.е. гипотеза принимается.

4. Проверка гипотезы о значимости корреляции

двух случайных выборок данных

Во многих случаях целью экспериментальных исследований является установление и изучение зависимости между измеряемыми величинами. К числу важных практических задач можно отнести оценку точности измерений при наличии статистической связи между погрешностями отдельных наблюдений, т.е. существовании корреляции между ними.

Для количественной оценки статистической связи по итогам эксперимента используется выборочный коэффициент корреляции. Так для выборок Х₁, Х₂, …Х_nи  Y₁, Y₂, …Y_n  коэффициент парной корреляции определяется выражением:

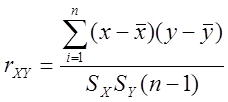.                                                          (4)

Причём справедливо следующее , а значение  свидетельствует об отсутствии линейной статистической связи между элементами двух выборок. Обычно величена коэффициента корреляции отлична от нуля и для корректного опыта на вопрос о коррелированности двух случайных величин проверяется гипотеза о значимости коэффициента корреляции, которая основана на статистике Стьюдента и t –критерий принятия гипотезы имеет вид:

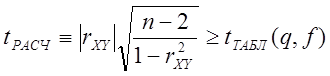,                                           (5)

где  - число степеней свободы.

Если расчётное значение критической статистики меньше граничного, найденного по таблице распределения Стьюдента, то корреляция не значима, т.е. между величинами Х и Y отсутствует линейная статическая связь.

Результаты расчётов для проведения проверки данной гипотезы

По формуле (4) рассчитываем выборочный коэффициент корреляции = 0,907443.

Рассчитываем t – критерий Стьюдента:

.

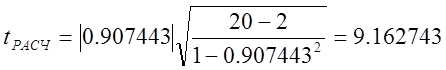Находим табличное значение t – критерия Стьюдента [1]  при q = 0,01  и  f = 18:

.

Так как , следовательно, коэффициент корреляции  значимо отличается от нуля, т.е. между величинами х и у существует линейная статистическая связь.

 Литература

1.  Пижурин А.А., Розенблит М.С. Исследолвания процессов деревообработки. – М.: Лесн. Промышленность, 1984. – 232 с.

2.  Львовский Е.Н. Статические методыпостроения эмперических формул. – М.: Высш. шк., 1988. – 239 с.

3.  Клюев А.С. Метрологическое обеспечение АСУ ТП / А.С. Клюев, А.Т. Лебедев,

Н.П. Миф. – М.: Энергоатмиздат, 1995. – 160 с.

4.  Наладка средств измерений и систем технического контроля. Справочное пособие \ под редакцией  А.С.Клюева.