Определенный интеграл и интегральные суммы, страница 2

В этом случае говорят, что произведено разбиение отрезка [a,b]. На каждом участке разбиения [x_i–1, x_i] возьмем произвольную точку c_i и вычислим значение функции f(x) в этих точках. Если умножить полученные значения функции f(c_i) на длину соответствующего участка  и просуммировать все это, то получим сумму

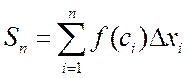,                                             (3.1)

которая называется интегральной суммой функции f(x) на отрезке [a,b].

Обозначим через  и введем фундаментальное понятие предела последовательности интегральных сумм и определенного интеграла.

Если предел последовательности интегральных сумм

.                                     (3.2)

существует, т.е. конечен и не зависит от способа разбиения отрезка [a,b] и от выбора точек c_i на соответствующих участках, то этот предел называется определенным интегралом функции f(x) на отрезке [a,b] и обозначают

.

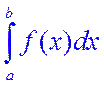Таким образом, по определению

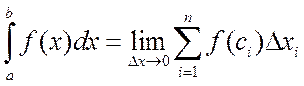                                         (3.3)

Здесь число a называется нижним пределом, число b называется верхним пределом интеграла.

Функция f(x) называется интегрируемой на отрезке [a,b], если для этой функции на указанном отрезке существует предел интегральных сумм, т.е. определенный интеграл.

Теперь возникает вопрос: какие функции интегрируемы, т.е. при каких условиях предел не зависит от способа разбиений и выбора промежуточных точек? Очевидно, что функция должна быть ограниченной (это есть необходимое условие интегрируемости функции), в противном случае она хотя бы на одном участке разбиения будет неограниченной и, следовательно, интегральная сумма по абсолютной величине будет сколь угодно большой и предел будет равен бесконечности. Отметим также (без доказательства) следующую теорему: если функция f(x) непрерывна на отрезке [a,b], то она интегрируема на этом отрезке (это есть достаточное условие интегрируемости функции).

Пример 3.1. С точностью до e=0,01 вычислить площадь криволинейной трапеции, ограниченной кубической параболой , осью Ox и прямыми x=0 и x=1 (рис. 3.3).

Решение. Разобьем отрезок [0; 1] на n разных частей. Найдём на каждом отрезке разбиения наименьшее значение функции , обозначим его m_i и построим прямоугольник с основанием  и высотой m_i. Его площадь равна

.

Объединение всех таких прямоугольников дает ступенчатую фигуру, «вписанную» в криволинейную трапецию (рис. 3.4). Площадь ступенчатой фигуры

.

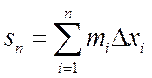Ясно, что S – площадь криволинейной трапеции – будет не меньше площади вписанной ступенчатой фигуры s_n для любого разбиения: .

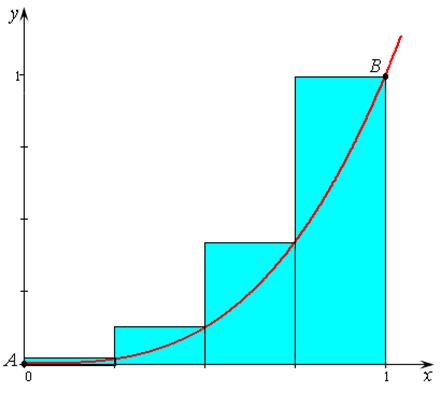
Если на каждом отрезке разбиения выбрать наибольшее значение M_i функции , то, поступая аналогичным образом, получим ступенчатую фигуру, описанную вокруг криволинейной трапеции (рис. 3.5).

Рис. 3.5

Площадь «описанной» ступенчатой фигуры

.

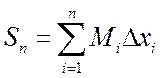Ясно, что S – площадь криволинейной трапеции – будет не больше площади описанной ступенчатой фигуры S_n для любого разбиения: .

Очевидно, что для любого разбиения отрезка интегрирования выполняется двойное неравенство .

Интуитивно ясно, что если разбиение сделать достаточно мелким, то площади вписанной и описанной ступенчатых фигур будут мало различаться. Понятно, что искомая площадь S приближенно равна площади вписанной или описанной фигур:  или , причем точность равенства увеличивается с измельчением разбиения. Разность  определяет точность вычислений. Чем больше точность, тем выше точность.

Для исходной функции будем вычислять нижние и верхние суммы  и , увеличивая число разбиений, занося результаты в таблицу.

n	2	4	10	50	100	500	1000
	0,063	0,141	0,203	0,24	0,245	0,249	0,2495
	0,563	0,391	0,303	0,26	0,255	0,251	0,2505

Точный результат равен 0,25.

Ясно, что такой способ нахождения площади криволинейной трапеции сопряжен с большим объемом вычислений. В следующей главе эту задачу мы решим с минимальными вычислениями, однако только после того, как будут изложены необходимые теоретические сведения.

3.3. Свойства определенных интегралов

Рассмотрим некоторые свойства определенных интегралов.

Начнём с линейного свойства, которое имеет аналог и для неопределенных интегралов:

Свойство 1.   .

Это свойство означает, что интеграл от суммы функций равен сумме интегралов от каждой функции и постоянный множитель можно выносить за знак интеграла. Данное свойство очевидно, если представить определенный интеграл в виде предела интегральной суммы.

Теперь рассмотрим свойства определенных интегралов, которые не имеют аналогов в случае неопределенных интегралов. Во-первых, обобщим определенный интеграл на случай, когда . Для этого можно воспользоваться следующим свойством.

Свойство 2.   .

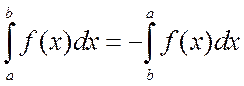Это свойство означает, что при перестановке пределов интегрирования определенный интеграл меняет знак. Действительно, здесь соответствующие интегральные суммы различаются по знаку, ибо в одной из них все Dx_i=x_i–x_i–1 положительны, а в другой аналогичные разности будут все отрицательны, поскольку порядок нумерации точек разбиения будет обратным.

Следствие. .

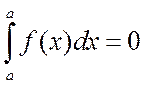Определенный интеграл с одинаковыми пределами интегрирования равен нулю. Эту формулу можно рассматривать как естественное распространение понятия определенного интеграла на отрезок нулевой длины.

Свойство 3. .

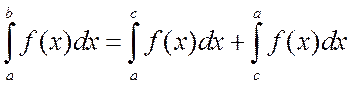Это свойство означает, что отрезок интегрирования можно произвольным образом разбивать на части и вычислять интеграл по каждой части отдельно. С геометрической точки зрения это свойство очевидно, поскольку означает, что площадь криволинейной трапеции равна сумме площадей каждой отдельной трапеции, которые получаются в результате разбиения ее вертикальными прямыми. Отметим также, что данное свойство справедливо при любых числах a, b, c, т.е. число c не обязательно должно находиться между числами a и b.

Свойство 4. Если функция f(x) – четная, то

,

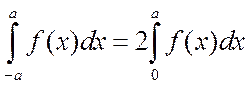если функция f(x) – нечетная, то

.

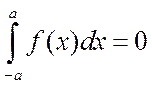Свойство 5. Если функции f(x)>0 на отрезке [a,b], то

.

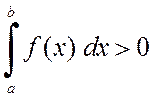Свойство 6. Если на отрезке [a,b] всюду выполняется неравенство f(x)³g(x), то

.

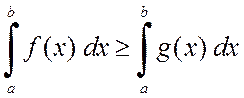Свойство 7. (Теорема об оценке определенного интеграла). Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a,b], то

.

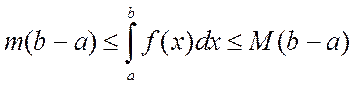Действительно, пусть на отрезке [a,b] выполняется неравенство m£f(x)£M, где m и M, тогда в соответствии со свойством 6 получим