Использование современной компьютерной техники и программного обеспечения для решения прикладных задач в области обогащения полезных ископаемых, страница 5

Поясним принцип получения уравнений материального баланса на примере рассмотрения всего процесса обогащения в целом. Общее количество материала на входе процесса должно быть равно сумме материала на выходах этого процесса. Поэтому можно составить уравнение

где M₀, M₁, M₃, M₄ – это количество материала соответственно на входе основной флотации, в хвостах, в промпродукте и в концентрате (см. рисунок 1).

 

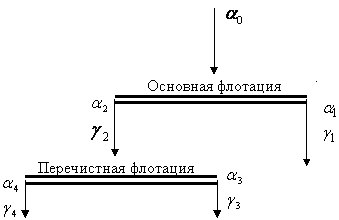Рис. 1. Двухстадиальная схема обогащения

Разделив обе части уранения на М₀, получим долевые выходы продуктов:

Материальный баланс по полезному компоненту для указанного выше процесса выражается уравнением

Для долевых выходов продуктов это даст следующее уравнение:

Таким образом, получены два уравнения для искомых величин .

Ещё два уравнения можно получить аналогично, рассматривая в качестве процесса одну из стадий обогащения.

В итоге получается система линейных алгебраических уравнений 4-го порядка. Её можно решить методом Гаусса, предварительно преобразовав исходную систему к стандартному виду.

Сформулируем алгоритм подпрограммы, реализующей метод Гаусса:

1.  Выполняем n-1 шагов прямого хода при k=1, 2, 3,…, n-1 (k –номер шага). Один ход прямого хода описан в пунктах 2 – 8. После окончания цикла по k перейдём к пункту 9.

2.  С помощью k-го уравнения исключаем неизвестную x_k из всех уравнений, начиная с (k-1)-го до n-го. Исключение x_k из i-го уравнения при i=k+1, k+2,…, n описано в пунктах 3 – 7. После окончания цикла по i перейдём к пункту 9.

3.  Вычисляем множитель m для i-го уравнения по формуле
, и полагаем a_ik=0.

4.  Подсчитываем новые коэффициенты при неизвестной x_j для j = k+1, k+2,…, n в i-м уравнении по формуле . После завершения цикла по j перейдём к пункту 6.

5.  Продолжаем цикл по j.

6.  Подсчитываем новый свободный член i-го уравнения по формуле .

7.  Продолжаем цикл по i.

8.  Продолжаем цикл по k.

9.  Начинаем обратный ход с вычисления x_n по формуле .

10.  При i = n-1, n-2,…,1 организуем цикл для нахождения остальных неизвестных. Один шаг этого цикла отражен в пунктах 11 – 13. После завершения цикла по i перейдём к пункту 14.

11.  Вычисляем сумму .

12.  Вычисляем значение неизвестной x_i по формуле .

13.  Продолжаем цикл по i.

В качестве результатов вычислений берём округлённые значения x₁, x₂,…, x_n.

1.2.  Содержательная формулировка задачи