2. Записать разложение данной дроби ![]() на сумму простейших дробей с
неопределенными (буквенными) коэффициентами, используя выражения вида (2.1.6) и
(2.1.5).
на сумму простейших дробей с
неопределенными (буквенными) коэффициентами, используя выражения вида (2.1.6) и
(2.1.5).
3. Полученное равенство умножить на общий знаменатель.
4. Для нахождения неопределённых коэффициентов можно воспользоваться одним из следующих способов.
Первый способ. Раскрыть скобки, привести подобные члены и приравнять коэффициенты при одинаковых степенях x.
Второй способ. Не раскрывая скобок, дать аргументу x столько различных значений, сколько имеется неопределенных коэффициентов.
5. Решить полученную систему линейных уравнений относительно искомых коэффициентов.
Пример 2.1.4. Разложить правильную дробь на сумму простейших дробей:
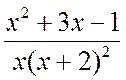 .
.
Решение. Поскольку знаменатель уже разложен на множители, то, в соответствие с этим разложением, записываем данную дробь в виде суммы простейших дробей:
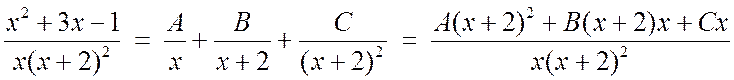 .
.
Приравниваем числители
![]()
1-й способ. Сравним коэффициенты при одинаковых степенях x:
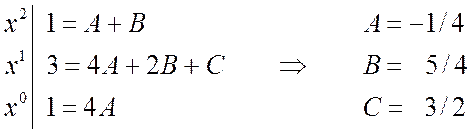
2-й способ. Будем придавать значениям x различные значения; лучше всего брать такие значения x, при которых некоторые слагаемые обращаются в ноль:
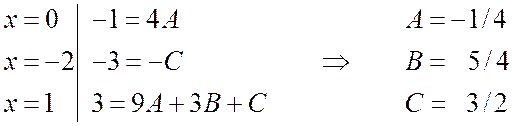
На практике обычно комбинируют оба способа, чтобы уравнения получались как можно проще. Например,
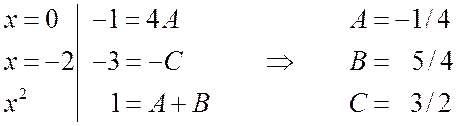
Итак, исходная правильная дробь следующим образом разлагается на сумму простейших дробей:
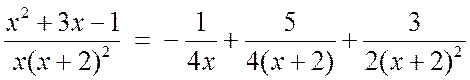 .
.
Пример 2.1.6. Найти разложение дробно-рациональной функции на сумму простейших дробей:
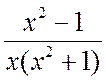 .
.
Решение. В соответствие с теоремой о разложении правильной дроби на сумму простейших дробей, получим:
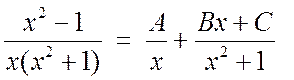 .
.
Приведем дроби к общему знаменателю и приравняем числители:
![]() .
.
Отсюда получаем
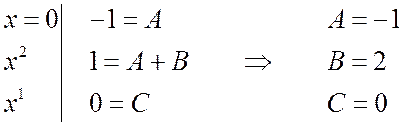
Таким образом, искомое разложение будет иметь вид
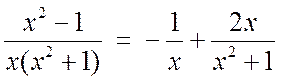 .
.
Подведём теперь итоги. Можно предложить следующую общую схему интегрирования рациональных функций.
1. Если рациональная дробь неправильная, то нужно выделить целую и дробную части при помощи правила деления многочленов.
2. Разложить знаменатель дроби на линейные и квадратичные множители.
3. Правильную рациональную дробь разложить на сумму простейших дробей при помощи метода неопределенных коэффициентов.
4. Вычислить интегралы целой части и полученных простейших дробей.
Данная схема показывает, что любая рациональная функция принципиально интегрируется в элементарных функциях. Однако это не означает, что этот путь является наилучшим, наиболее экономным. Как правило, существует несколько приёмов вычисления конкретных интегралов и всякий раз те или иные обстоятельства должны подсказать тот искусственный прием, который быстрее всего приводит к цели. Наша цель – показать, что рациональные функции всегда «берутся», т.е. для неё всегда можно найти первообразную и эту первообразную можно записать при помощи элементарных функций. Приведённая схема показывает, как в принципе это всегда можно сделать. Рассмотрим несколько примеров.
Пример 2.1.7. Вычислить интегралы:
а) 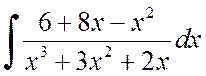 , б)
, б) 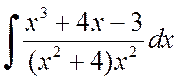 , в)
, в) 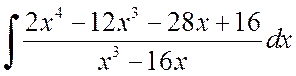 .
.
Решение. а) Подынтегральная дробь правильная, поэтому разложим знаменатель на множители:
![]() .
.
После этого разложим подынтегральную рациональную дробь на сумму простейших дробей при помощи метода неопределённых коэффициентов.
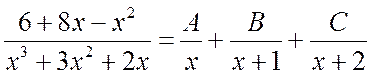 .
.
Приведем дроби к общему знаменателю и приравняем числители:
![]() .
.
Отсюда получаем
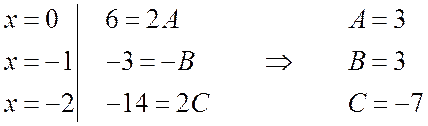
Таким образом, искомое разложение будет иметь вид
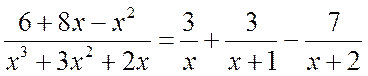 .
.
Теперь вычисляем интеграл:
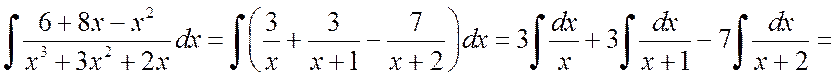
![]() .
.
б) Подынтегральная дробь правильная и знаменатель уже разложен на множители. Поэтому сразу приступаем к разложению подынтегральной дроби на сумму простейших дробей:
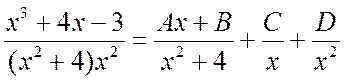 .
.
Приведем дроби к общему знаменателю и приравняем числители:
![]() .
.
Отсюда получаем
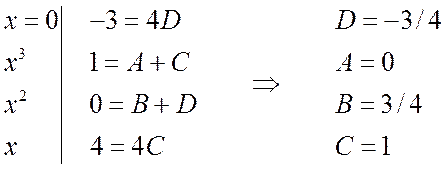
Следовательно, искомое разложение будет иметь вид
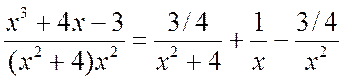 .
.
Теперь вычисляем интеграл:
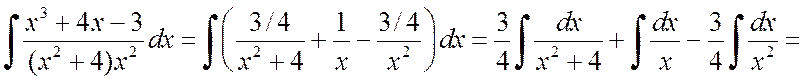
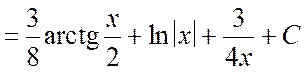 .
.
в) Подынтегральная дробь является неправильной. Поэтому выделим целую и дробную части при помощи деления многочленов «уголком»:
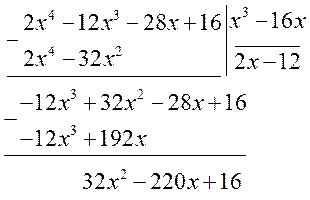
В результате, получаем
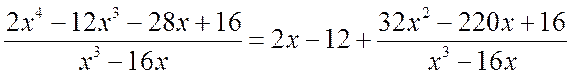 .
.
Теперь разложим знаменатель на множители:
![]() .
.
После этого разложим правильную рациональную дробь на сумму простейших дробей:
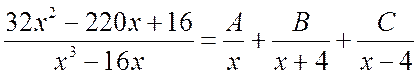 .
.
Приведем дроби к общему знаменателю и приравняем числители:
![]() .
.
Отсюда получаем
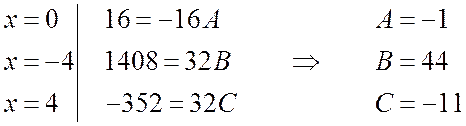
Таким образом, искомое разложение будет иметь вид
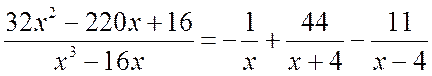 .
.
Теперь вычисляем интеграл:
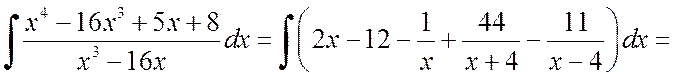
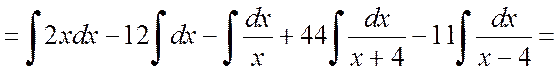
![]() .
.
1. Какие функции называются рациональными.
2. Какие рациональные дроби называются правильными, а какие не правильными?
3. Как представить неправильную дробь в виде суммы целой части и правильной дроби? Опишите на примере алгоритм деления многочленов «уголком».
4. Какие правильные рациональные дроби относятся к простейшим?
5. Покажите, как проинтегрировать простейшую дробь третьего типа.
6. Что значит разложить многочлен на линейные и квадратичные множители? Всегда ли это можно сделать?
7. Как разложить правильную рациональную дробь на сумму простейших дробей? Опишите метод неопределенных коэффициентов.
1. Вычислить интегралы от простейших дробей:
|
а) |
б) |
в) |
г) |
2. Вычислить интегралы от неправильных дробей:
|
а) |
б) |
в) |
г) |
3. Вычислить интегралы, используя метод неопределенных коэффициентов:
|
а) |
б) |
в) |
г) |
4. Вычислить интегралы, используя метод неопределенных коэффициентов:
|
а) |
б) |
в) |
г) |
5. Вычислить интегралы, используя метод неопределенных коэффициентов:
|
а) |
б) |
в) |
г) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.