Московскийгосударственныйуниверситет
путейсообщенияРФ (МИИТ)
Кафедра «Физика-2»
Группа_______УПП – 141 _______________Кработедопущен____________________
(Дата,подпись преподавателя)
Студент _____АтрощенкоА.Л____________Работавыполнена___________________
(ФИОстудента)(Дата, подписьпреподавателя)
Преподаватель____ПыкановИ.В.________ Отчётпринят_______________________ (Дата, подписьпреподавателя)
ОТЧЁТПОЛАБОРАТОРНОЙРАБОТЕ№____72____
СНЯТИЕКРИВОЙНАМАГНИЧИВАНИЯИПЕТЛИГИСТЕРЕЗИСАФЕРРОМАГНИТНЫХВЕЩЕСТВСПОМОЩЬЮОСЦИЛЛОГРАФА
(Название лабораторной работы)
1. Цельработы:
Получитьнаэкранеосциллографапетлюгистерезиса, измеритьеепараметры, снять_кривуюна_магничивания_______________________________________________
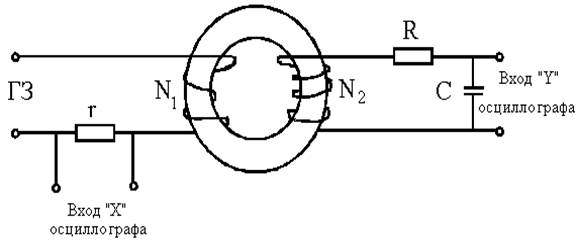
2. Принципиальнаясхемаустановки (илиеёглавныхузлов):
Рис 1 – схемаосциллографа
|
Все вещества обладают магнитными свойствами, которые обнаруживаются при помещении их во внешнее магнитное поле B0. В этом поле они намагничиваются и создают дополнительное магнитное поле B’. Результирующее поле в веществе будет равно:
B=B0+B’.
Рассмотрим причину возникновения дополнительного магнитного поля. Известно, что контур с током характеризуется магнитным моментом
pm=IS,
где I - сила тока в контуре; S - площадь, ограниченная контуром.
Электрон в атоме движется вокруг ядра, поэтому его можно рассматривать как некоторый контур с током и рассчитать его орбитальный магнитный момент pl. Классический расчет для круговой орбиты дает
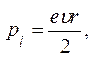
где e-заряд электрона; u- его линейная скорость; r-радиус орбиты.
Если
учесть
условие
стационарности
орбит
электрона
в
теории
атома,
данной
Бором
(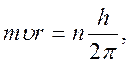 где
n=1,2,3,...), то орбитальный
магнитный
момент
электрона
можно
записать
так:
где
n=1,2,3,...), то орбитальный
магнитный
момент
электрона
можно
записать
так:
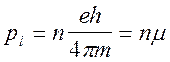 в,
в,
Величина
![]() в
= 0,927 10-23 А×м2 служит
единицей
измерения
магнитных
моментов
микрочастиц;
ее
называют
магнетоном
Бора.
в
= 0,927 10-23 А×м2 служит
единицей
измерения
магнитных
моментов
микрочастиц;
ее
называют
магнетоном
Бора.
Более точный расчет орбитального магнитного момента электрона в атоме дает квантовая механика. Согласно ее результатам
pl = ![]() в
в
![]()
где l – целое число, например, 0,1,2,....
Кроме орбитального, электрон обладает еще собственным (спиновым) магнитным моментом, связанным с существованием у него собственного момента количества движения (спина). Спиновый магнитный момент электрона равен
ps=![]() в
в![]() ,
,
Полный магнитный момент атома p равен векторной сумме магнитных моментов всех составляющих его частиц. При этом сложение происходит по квантовым законам. Ядра атомов также обладают магнитными моментами, но по сравнению с магнитными моментами электронов ими можно пренебречь.
Магнитное поле вещества зависит от ориентации магнитных моментов атомов. Если все моменты расположены хаотично, то магнитное поле B’ отсутствует. При частичной или полной упорядоченности магнитных моментов в веществе создается магнитное поле B’.
Характеристикой магнитного состояния вещества является вектор намагничения или намагниченность J .По определению
J=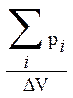 ,
,
где DV- объем, в пределах которого суммируются полные магнитные моменты атомов.
Будем исходить из того, что магнитное поле в веществе создается макротоками, т.е. токами в проводниках I, и микротоками I¢, определяющими величину J. Таким образом, полная индукция является функцией макротоков и намагниченности вещества.
Расчет индукции B сложен, так как B зависит не только от свойств вещества, но и от формы и размеров образца.
Во многих случаях расчет упрощается введением еще одной характеристики магнитного поля - вектора напряженности магнитного поля H, по определению равной
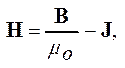 (
1)
(
1)
где mo - магнитная постоянная.
Вектор H обладает тем свойством, что его циркуляция в произвольном поле и в любых магнитных веществах зависит только от макротоков I,
![]() Hdl=
Hdl=![]() , (2)
, (2)
( закон полного тока в магнитных средах, токи I протекают через площадь, охватываемую контуром “k” ).
В вакууме, где нет микротоков,
H=B/mo.
Если для данного вещества экспериментально получить зависимость J=J(H), которая одинакова для образцов любой формы и размеров, и рассчитать по формуле (2) H, то на основании уравнения (1) можно найти индукцию магнитного поля в веществе.
Экспериментально наиболее просто J=J(H) определяется для образца в виде тороида, на который равномерно нанесены витки провода. Действительно, если в проводнике идет ток I, а общее число витков составляет N и длина тороида L, то на основании формулы (2) получаем
![]() H
dl=
HL=
NI,
H
dl=
HL=
NI,
откуда
H=NI/L, (3)
т.е. величина H может быть легко рассчитана.
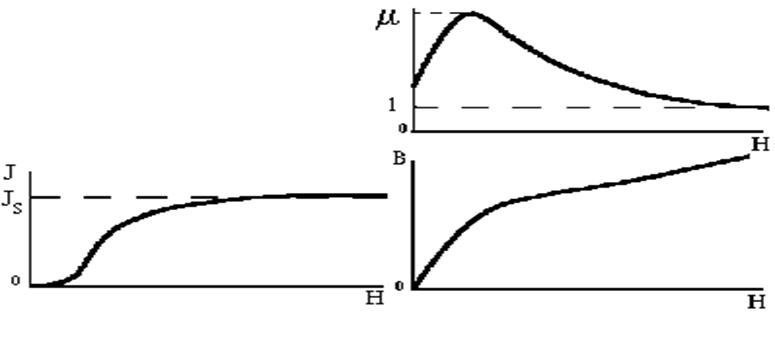
Рис. 2 Рис. 3
Измеряя для каждого H величину намагниченности J, находим зависимость J=J(H) (рис.2). На рисунке Js есть намагниченность насыщения, соответствующая случаю, когда все магнитные моменты атомов ориентированы по направлению магнитного поля.
Выразим связь между J и H в виде
J=c H, (4)
где c - магнитная восприимчивость вещества.
Тогда из формул (1) и (4) следует:
B=moH+moJ=moH(1+c). (5)
Величину (1+c) обозначают m и называют магнитной проницаемостью вещества. Следовательно, связь между B и H записывается в виде
B=momH.
Для ферромагнитных веществ график зависимости B=B(H) дан на рис.3. Кроме того, на рис.2 дается зависимость m от H. Как видно из графика, с увеличением Hиндукция увеличивается. Рост индукции B в веществе после достижения намагниченности насыщения Js объясняется дальнейшим увеличением напряженности поля (см. формулу (5)).
По своим магнитным свойствам ферромагнетики существенно отличаются от пара- и диамагнетиков* . В частности, их относительная магнитная проницаемость может достигать величины 104¸105, они могут обладать также и остаточной намагниченностью.
Эти особенности невозможно объяснить с позиции классической физики. Объяснение явления ферромагнетизма дала лишь квантовая механика. В квантовой теории считается, что под действием так называемых обменных сил магнитные моменты отдельных атомов должны выстраиваться параллельно друг другу. При этом в кристалле образуются области спонтанного, самопроизвольного намагничивания, которые носят название доменов. В пределах каждого домена (размер домена порядка 1–10 мкм) ферромагнетик намагничен до насыщения. В отсутствии внешнего поля в ферромагнетике, как правило, наблюдается образование большого количества доменов. Такая ситуация энергетически более выгодна по сравнению со случаем, когда имеется, например, лишь один домен, поскольку сведено до минимума рассеяние магнитного поля в пространство вне ферромагнетика, причем направления магнитных моментов для разных доменов различны, так что суммарный момент может быть равен нулю. Все зависит от предыстории образца.
Остановимся теперь на объяснении хода зависимости B=f(H) для ферромагнетика.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.