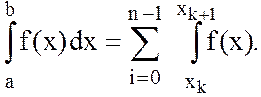Математическое моделирование систем и процессов. Часть 4: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 2

                                       (11.3)

          Выбор квадратурной формулы определяется классом функции , формой ее задания, набором узловых значений {x_k} и  классом интерполирующей  функции 

          Элементарные  квадратурные  формулы проще всего выводятся  исходя из геометрической трактовки  интеграла. Рассмотрим некоторые из них.

11.2. Обзор  классических  методов  численного  интегрирования

          Метод  прямоугольников.  Интервал  интегрирования  разбивают на  n  равных  частей  точками  x_k (k = 0, 1, 2, … , n); x₀ = a; x_n = b. Длина каждого из отрезков  равна 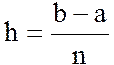. Значения подынтегральной функции   в узлах  x_k обозначают

               (11.4)

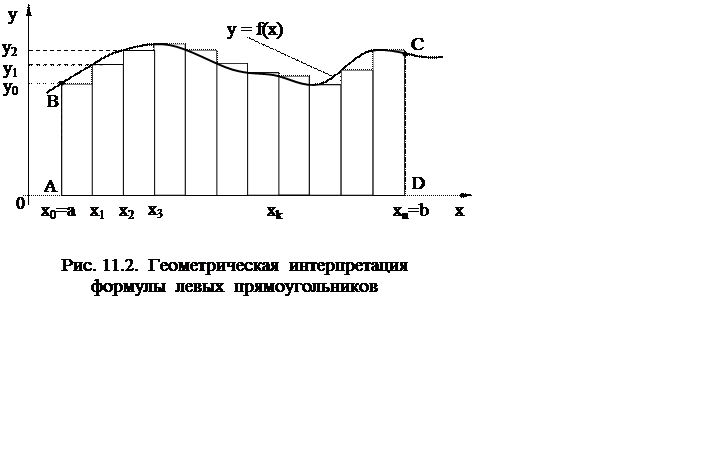
          Функцию  заменяют ступенчатой функцией, которая в пределах каждого элементарного отрезка  принимает постоянное значение, равное, например, значению  подынтегральной функции   на левом  конце  отрезка, т. е.  Геометрически это означает, что на интервале  частичный интеграл (см. формулу 11.3) приближенно определяется как площадь  элементарного  прямоугольника (рис. 11.2):

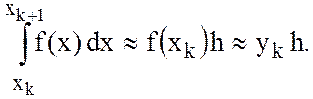                                    (11.5)

          Тогда  площадь криволинейной трапеции ABCD, определяющая значение  искомого интеграла 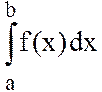, приближенно заменяется суммой площадей n  прямоугольников с высотами  y_k  и основаниями  h, что выражается формулой:

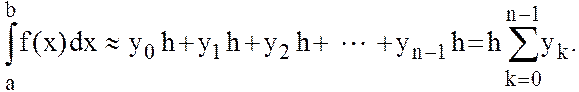                 (11.6)

которая называется  квадратурной формулой левых прямоугольников.  

          Данный метод дает достаточно грубую оценку искомого интеграла. Его  методическая  погрешность определяется соотношением

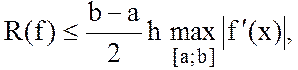                                   (11.7)

т. е. для непрерывно дифференцируемых функций она убывает по линейному закону с уменьшением  величины шага h. Следовательно, метод имеет первый порядок  точности.

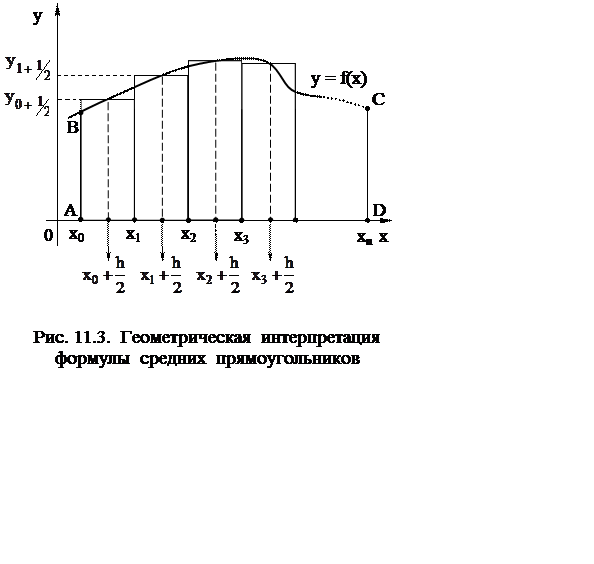          Более точный  результат вычисления определенного интеграла можно получить, если площадь криволинейной  трапе-ции ABCD заменить суммой площадей n прямоугольников с высотами, равными  значениям  подынтегральной  функции  в средней  точке  элементарного отрезка  (рис. 11.3).

          Обозначим середину отрезка  как 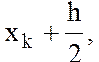  а  значение функции  в этой точке − 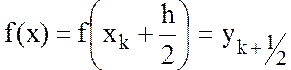. Получаем  квадратурную формулу  средних  прямоугольников 

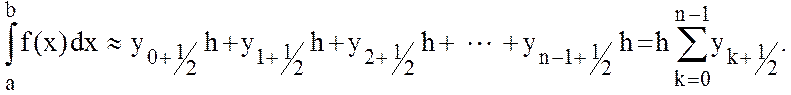    (11.8)

          Методическая погрешность метода средних прямоугольников для тех случаев, когда подынтегральная функция  имеет непрерывную вторую производную, определяется соотношением

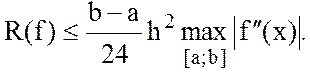                                    (11.9)

Таким образом погрешность убывает прямо пропорционально величине h². Следовательно, метод имеет второй порядок точности.

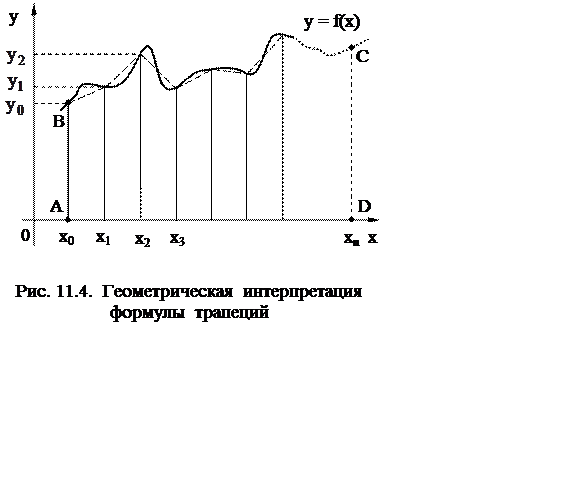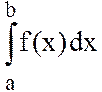Метод  трапеций. Подынтегральную функцию  заменяют кусочно-линейной функцией.  Геометрически это означает, что в пределах каждого элементарного отрезка  функция  аппроксимируется прямой  линией, проходящей  через  две соседние точки с координатами [x_k; f(x_k)] и [x_k+1; f(x_k+1)] (рис. 11.4). Это дает возможность площадь криволинейной трапеции ABCD, определяющую  значение искомого интеграла , приближенно заменить суммой  площадей n элементарных  трапеций. Учитывая, что площадь такой трапеции определяется  как  произведение  полусуммы оснований  на  высоту:

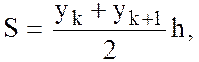                                            (11.10)

получаем   квадратурную формулу  трапеций:

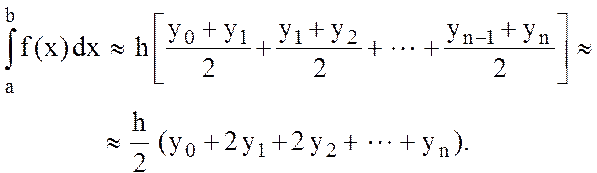              (11.11)

          Формула (11.11) может быть выведена и другим способом − с применением математического аппарата интерполирования. При этом в формуле (11.3)подынтегральная функция  на частичном отрезке  заменяется интерполяционным  многочленом Лагранжа первой степени, построенным на узлах  :

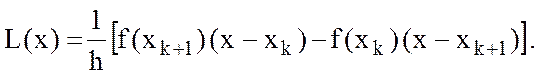                  (11.12)

          Методическая погрешность метода  трапеций оценивается  как

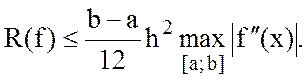                                  (11.13)

Метод  имеет  второй  порядок  точности, так как его погрешность убывает прямо пропорционально величине h².

          Метод  Симпсона. Интервал интегрирования  разбивают на четное количество равных отрезков. На каждых  двух смежных  элементарных отрезках  подынтегральную функцию  заменяют интерполяционным полиномом второй степени  либо интерполяционным многочленом Лагранжа второй степени, построенным на узлах  Геометрически  это означает, что в пределах частичного сдвоенного интервала  подынтегральная функция  заменяется  параболой, проходящей через три соседние точки с координатами [x_k; f(x_k)],  [x_k+1; f(x_k+1)]  и  [x_k+2; f(x_k+2)]   (рис. 11.5).

          Таким образом, площадь исходной криволинейной трапеции приближенно заменяется суммой  n  площадей  элементарных  криволинейных  трапеций.

              Квадратурная формула  Симпсона  имеет  вид:

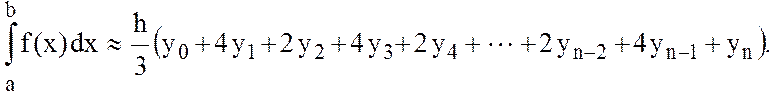    (11.14)

          Методическая погрешность  метода Симпсона для тех случаев, когда подынтегральная функция  имеет непрерывную четвертую производную, определяется  соотношением

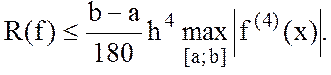  (11.15)

          Метод имеет четвертый  порядок  точности.

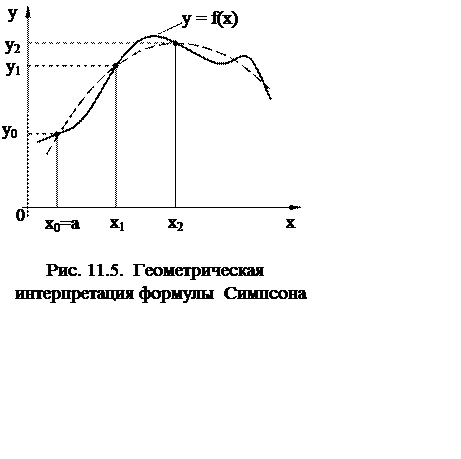          Следует подчеркнуть, что сложно дать однозначную оценку рассмотренных методов с точки  зрения их точности. Точность численного интегрирования в каждой конкретной задаче зависит от характера изменения (свойств) подынтегральной функции  и поведения ее производных на интервале интегрирования . Так например, метод Симпсона обеспечит значительное преимущество над другими методами по точности результата только при условии, что четвертая производная функции  не будет слишком  велика. В противном случае метод трапеций  и средних прямоугольников  дадут существенно более точный  результат.

          Квадратурные формулы прямоугольников (11.6), (11.8), трапеций (11.11), Симпсона (11.14) являются частными случаями формул  Ньютона-Котеса, в основе которых лежит замена подынтегральной функции интерполяционным многочленом Лагранжа. В методе Эйлера подынтегральная функция замещается интерполяционным многочленом Эрмита. Методы  Гаусса-Кристоффеля предполагают использование полиномов Лежандра и неравноотстоящих узлов, выбираемых из расчета минимума погрешности интегрирования. Различные подходы к формированию квадратурных формул реализованы в методах Чебышева, Маркова, Ромберга  и  др.

11.3.  Метод  Монте-Карло  (метод  статистических  испытаний)

          Суть  метода  Монте-Карло (метода  статистических  испытаний)заключается в следующем. Для решения вычислительной задачи  подбирается соответствующая  вероятностная модель, в которую входит искомое неизвестное число. Проводятся статистические испытания данной вероятностной модели с последующей статистической обработкой результатов ее многократных «наблюдений». В итоге получают оценку искомой величины. Иными словами моделируются входные случайные последовательности с заданными законами  распределения. Каждый элемент входной последовательности преобразуется по алгоритму, соответствующему поставленной задаче. Полученная в итоге преобразований  выходная случайная последовательность подвергается статистической обработке для определения той вероятностной характеристики, которая принимается за оценку искомой  величины. Чаще всего такой  вероятностной характеристикой  является  математическое ожидание.