Сопротивление материалов. Часть 3: Методические указания к выполнению контрольных работ, страница 4

Поперечное сечение стержня состоит из четырех неравнобоких уголков 45 × 28 × 3 и прямоугольника с высотой  h,  равной 12 см, и шириной  b,  равной
1,2 см (рис. 3.3).

Решение.

Поскольку сечение дважды симметричное, то оси симметрии z и y являются главными осями
составного сечения. Проведем для каждого сечения собственные оси. Для прямоугольного сечения
собственные оси z₁, y₁ совпадают с главными
осями – z, y.

Оси для неравнобокого уголка проходят через его центр тяжести и обозначаются  z₂, y₂.

Общее сечение состоит из различных фигур. Определим их геометрические характеристики.

Рассмотрим прямоугольное сечение (рис. 3.4).

Площадь сечения  Моменты инерции
рассчитаем по формулам:

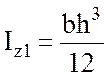                         ;                   (3.7)  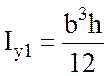                    .                              (3.8)

Рис. 3.3. Поперечное сечение стержня                 Рис. 3.4. Прямоугольное сечение

После подстановки исходных данных в формулы (3.7), (3.8) получим:  

Рассмотрим неравнобокий уголок.

Для неравнобокого уголка геометрические характеристики выбираются из сортамента [3].

Для уголка  (рис. 3.5, a)            

 

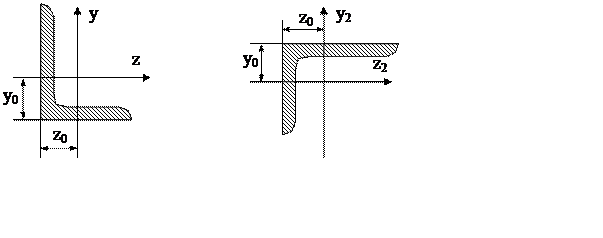а                                             б

Рис. 3.5. Неравнобокий уголок

В рассматриваемом случае в составном сечении неравнобокий уголок развернут на 90° по отношению к его положению в сортаменте, поэтому необходимо в соответствии с его положением изменить обозначения (рис. 3.5, б):     

Вычислим моменты инерции составного сечения [2, подразд. 3.1]:

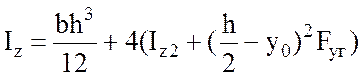                                 ;    (3.9)

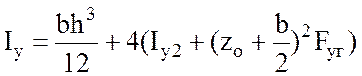                                 .  (3.10)

После подстановки исходных данных в уравнения (3.9), (3.10) получим:

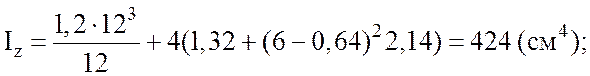
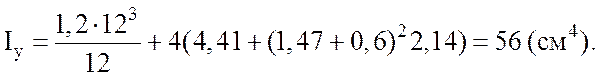
Учитывая, что  вычислим минимальный радиус инерции и гибкость стержня (3.1):

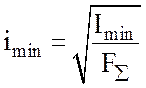                      ;               (3.11) 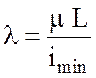                       .                             (3.12)

После подстановки исходных данных в формулы (3.11), (3.12) получим: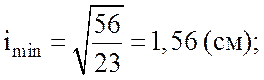   

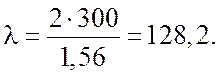
Из справочной таблицы  выписываем: при  λ = 120  φ = 0,45;  при λ = 130
φ = 0,40.

Для того чтобы найти значение φ для λ = 128,2, интерполируем внутри отрезка изменения гибкости от 130 до 120 единиц: 130 – 120 = 10; 0,45 – 0,4 =
= 0,05, тогда на единицу гибкости приходится 0,005 единиц φ, а на 8,2 единиц гибкости поправка составит 0,041.

С учетом поправки для λ = 128,2  φ = 0,45 – 0,041 = 0,409.

Допускаемую нагрузку определяем исходя из условия устойчивости (3.6):  

Поскольку λ = 128,2 > 100, критическая нагрузка рассчитывается по формуле Эйлера (3.2):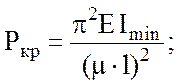  

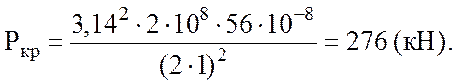
Коэффициент запаса устойчивости определим из выражения (3.5):

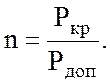                                                                        (3.13)

После подстановки исходных данных в формулу (3.13) получим:

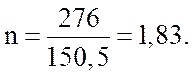
4. ДИНАМИЧЕСКОЕ  ДЕЙСТВИЕ  НАГРУЗОК

4.1. Основные теоретические сведения

Нагрузка, сравнительно быстро меняющая свою величину или положение, называется динамической.

Общий метод расчета, учитывающий динамическую нагрузку, основан на принципе Даламбера, согласно которому движущееся тело можно рассматривать находящимся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции.

При вращательном движении с постоянной угловой скоростью ω сила инерции определяется по формуле:

                                                                           (4.1)

где m – масса движущегося тела;

 – центростремительное ускорение;

R – радиус вращения.

Сила инерции всегда направлена в сторону, противоположную ускорению.

Угловая скорость выражается через число оборотов:

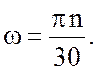                                                                            (4.2)

Если силы инерции известны, то для расчета конструкции применяют обычный метод сечений, а для определения внутренних усилий используют уравнение равновесия.

При действии ударной нагрузки (нагрузки чрезвычайно малой продолжительности) определение сил инерции затруднительно. Примером ударного
нагружения является удар падающего груза при забивке свай и т. п.

При ударном воздействии груза Р на конструкцию напряжения в ней
могут значительно превосходить напряжения в той же конструкции при стати-ческом приложении нагрузки Р. Напряжения, возникающие при ударном
нагружении, называют динамическими и определяют их по формуле:

                                               ,                  (4.3)

где  – статические напряжения;

 – коэффициент динамики.

Коэффициент динамики вычисляют в зависимости от высоты падения груза h и статического прогиба  в точке падения груза:

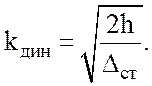                                                                    (4.4)

Статические напряжения и прогиб в точке удара определяют согласно формулам теории изгиба прямых стержней [2, разд. 4].

4.2. Решение типовой задачи при ударных воздействиях на конструкцию

На двутавровую балку (двутавр № 20а, , ), свободно лежащую на двух опорах (рис. 4.1, а), с высоты h, равной 11 см, падает груз Р весом 300 Н.

Найти наибольшие нормальные напряжения в балке. Решить аналогичную задачу при условии, что правая опора заменена пружиной, податливость  (осадка от груза весом 10 кН) которой равна

1) Для определения наибольшего нормального напряжения в балке сначала приложим вес падающего груза в виде сосредоточенной силы Р в точку падения балки (рис. 4.1, б), с помощью уравнений статики определим реакции опор R_А и R_В и построим эпюру изгибающих моментов M_z [2, подразд. 4.2, 4.3].

По значению наибольшего изгибающего момента вычислим статические напряжения:

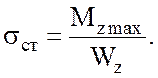                                                                   (4.5)

После подстановки значений W и  (рис. 4.1, в) в формулу (4.5)
получим: 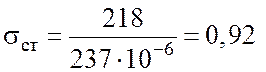(МН/м²).