




Для расчетов и проектирования систем передачи надо уметь сигналы задавать в виде математических представлений.
Первый вид задания, наиболее понятный, в виде функции
времени. Реальные сигналы в такой форме просматривают на осциллографе.
Второй способ задания – задание в виде спектра сигнала.![]()
Пусть имеется произвольная функция времени S(t) на
конечном интервале (t1, t2) и есть ортогональная система
функций ![]() . (т.е.
. (т.е.![]()
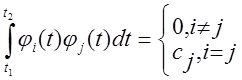 ).
).
Утверждается, что
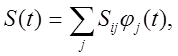 где
где 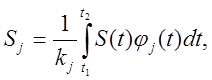
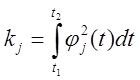 .
.
Это означает, что функция, заданная на конечном временном интервале, представима в виде ряда по системе ортогональных функций. Если функция периодическая, то она также представляется этим рядом.
Наиболее часто в качестве ортогональной системы
функций берутся тригонометрические функции ![]()
![]() . Тогда получается тригонометрический
ряд Фурье:
. Тогда получается тригонометрический
ряд Фурье:
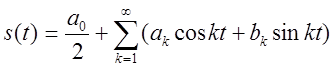
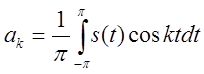 ,
, 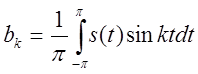 , k=0,1,2
, k=0,1,2
Если воспользоваться формулами Эйлера и перейти к комплексной переменной, то получим экспоненциальную форму ряда Фурье:
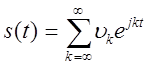 ,
, 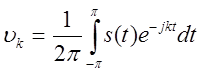 ,
, ![]() (формула
Эйлера).
(формула
Эйлера).
Набор коэффициентов ak , bk или
![]() k называют амплитудным
спектром сигнала.
k называют амплитудным
спектром сигнала.
Большая часть реальных сигналов требует задания на бесконечном промежутке времени и не является периодическими. Чтобы представить такие сигналы используются прямое и обратное преобразование Фурье или спектральную плотность:
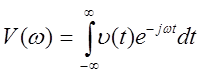 - спектр функции
- спектр функции ![]() (t) или прямое преобразование
Фурье.
(t) или прямое преобразование
Фурье.
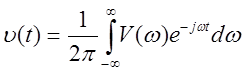 - обратное
преобразование Фурье.
- обратное
преобразование Фурье.
Таким образом, сигнал может быть задан либо как функция времени (временное представление), либо спектром этой функции (частотное представление).
Перечислим основные свойства преобразования Фурье,
которые дают возможность упростить расчет спектров функционально связанных
сигналов. Будем обозначать символически прямое преобразование Фурье как F
{v(t)}, а обратное F-1 {V(![]() )}.
)}.
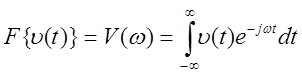
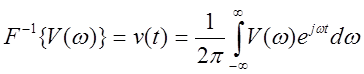
1. Свойство изменения масштаба
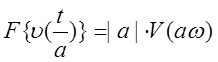 ,
a – действительное число
,
a – действительное число
2. Свойство линейности
![]()
3. Свойство симметрии
![]()
4. Теорема запаздывания
![]()
5. Теорема модуляции
![]()
6. Свойство дифференцирования
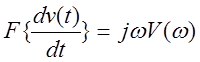 или
или
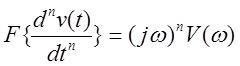
7. Свойство интегрирования
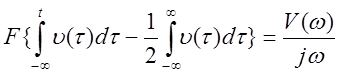
8. Теорема о свертке функций
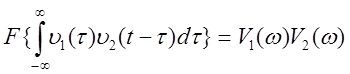
9. Теорема о спектре произведения
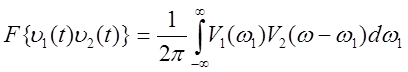
10. Теорема Рэлея (энергия сигнала равна энергии спектра)
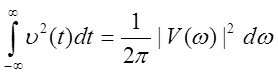
Для существования ряда Фурье требуется абсолютная
интегрируемость функций, т.е. 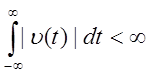 . Широко
распространенные модели сигналов в радиотехнике, такие как единичный скачок
u(t), гармоничное колебание
. Широко
распространенные модели сигналов в радиотехнике, такие как единичный скачок
u(t), гармоничное колебание ![]() , не обладают
свойством абсолютной интегрированности, и в строгом смысле не обладают
преобразованием Фурье. Чтобы эту трудность обойти прибегают к искусственному
приему. Один из способов преодолеть эту трудность сводится к введению
несколько необычной функции Дирака или
, не обладают
свойством абсолютной интегрированности, и в строгом смысле не обладают
преобразованием Фурье. Чтобы эту трудность обойти прибегают к искусственному
приему. Один из способов преодолеть эту трудность сводится к введению
несколько необычной функции Дирака или ![]() -
функции (единичный импульс) – другое ее наименование.
-
функции (единичный импульс) – другое ее наименование.
Определим эту функцию, задав ее свойства:
1. 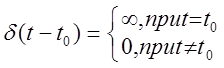
2. ![]() - симметричность (четная относительно
t0)
- симметричность (четная относительно
t0)
3. 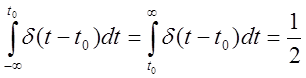 , т.е.
, т.е. 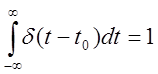
4. 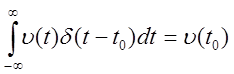 - фильтрующее свойство.
- фильтрующее свойство.
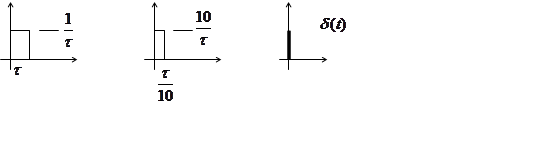 Физически эту
функцию можно представить себе как предельную последовательность обычных
функций. Например, прямоугольных импульсов, имеющих площадь равную единице,
когда
Физически эту
функцию можно представить себе как предельную последовательность обычных
функций. Например, прямоугольных импульсов, имеющих площадь равную единице,
когда ![]() .
.
Можно взять и функцию отсчетов 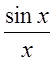 , тогда
, тогда
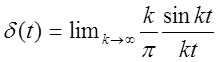
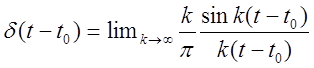
, при ![]()
![]()
Обратное
преобразование определим формально – это ![]() -
функция.
-
функция.
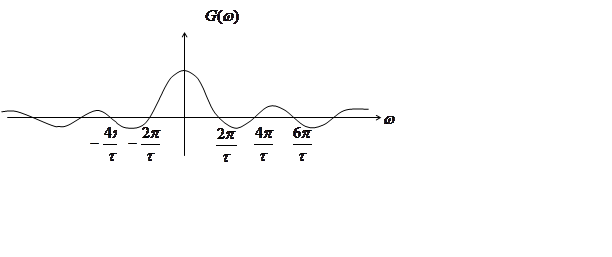
Стробирующая функция
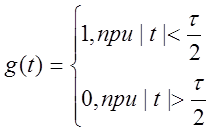
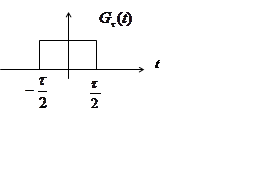 |

Преобразование Фурье от постоянной составляющей ![]() (t)=A найдем как предел стробирующей
функции с амплитудой А при
(t)=A найдем как предел стробирующей
функции с амплитудой А при ![]() .
.
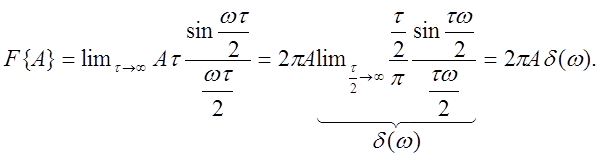
Гармонический сигнал
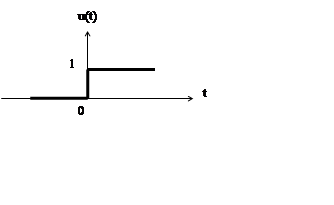
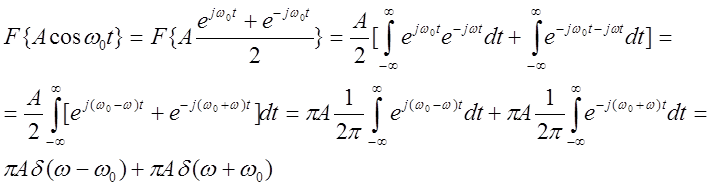
Единичный скачок
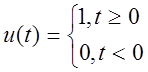
Представим u(t) в виде 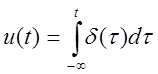 .
.
Вычтем среднее значение 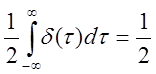 ,
получим
,
получим 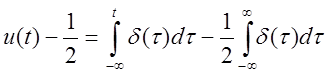 .
.
Согласно теореме интегрированности по времени
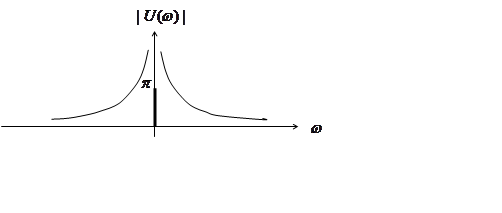
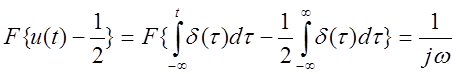 , т.е.
, т.е.
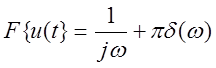
Часто сигнал можно аппроксимировать кусочно-линейной ломаной или отрезками параболы. Тогда можно, продифференцировав сигнал, перейти к спектру сигналов, представляющих собой единичную импульсную функцию и задача нахождения спектра существенно упростится. Найдите с помощью этого приема спектры сигналов:
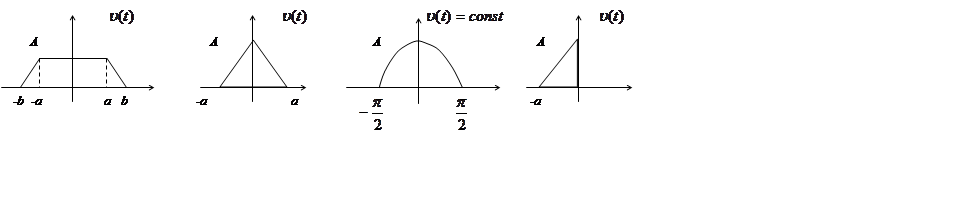 |
Теорема устанавливает возможность полного восстановления детерминированного сигнала с ограниченным спектром по его отсчетам и указывает предельное значение времени между отсчетами, при котором такое восстановление еще возможно. Непрерывный сигнал, таким образом, может быть задан в цифровой форме в виде последовательности мгновенных значений. Это третий способ математического задания сигналов, который принципиально важен. Он позволяет рассматривать передачу любого сообщения и дискретного и непрерывного с единой позиции как передачу чисел (данных).
Сеть связи, следовательно, можно иметь единую интегрированную для всех систем электросвязи, равно как и другой общий принцип коммутации на АТС посредством адресации данных через общую память.
Формулировка теоремы Котельникова следующая: Если непрерывная функция времени имеет спектр, ограниченный полосой частот от 0 до F Гц, удовлетворяет условиям Дирихле, то она полностью определяется своими мгновенными значениями, отстоящими друг от друга на 1/F с.
Надо заметить, однако, что модель сигналов с ограниченным спектром имеет одно теоретическое неудобство, она не может отображать основное свойство сигнала – способность нести информацию. Причина – возможность теоретического предсказания поведения функции с ограниченным спектром на всей оси времени, если она точно известна на сколь угодно малом отрезке времени. Указанное недоразумение устраняется, если рассматривать теорему Котельникова как приближенную для функций с неограниченным спектром.
При восстановлении аналогового сигнала возникают погрешности, вызванные принудительным ограничением спектра сигнала и конечностью числа используемых отсчетов. Оценка этих погрешностей имеется во многих источниках, например, И.А. Цикин. Свойства сигналов, используемых в радиосистемах. Л.ЛПИ, 1980-66 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.