Термогидравлический модуль РАТЕГ: модели, методы решения, страница 13

φ_ij - коэффициент видимости (падающая на элемент i доля энергии, излучаемой элементом j)

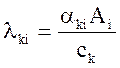 - объемный коэффициент теплопереноса от фазы к межфазной поверхности, кг⋅с^-1⋅м^-3

µ_k – динамическая вязкость, Н⋅с⋅м

r = a_g r_g + a_f r_f – плотность теплоносителя, кг⋅м

ρ_k – плотность фазы, кг⋅м

r^/_n =r_gX_n –парциальная плотность неконденсируемого газа n в газовой фазе, кг⋅м

ρ_ks - плотность фазы k в состоянии насыщения, кг⋅м

ξ_loc – коэффициент местного гидравлического сопротивления

σ_r = 5.67⋅10^-8 вт/м²К⁴ – постоянная Стефана-Больцмана

σ_fg – коэффициент поверхностного натяжения на границе жидкость-пар, Н⋅м

τ_ik– сила трения между фазой и межфазной границей, отнесенная на единицу объема, Н⋅м

τ_wk – сила трения на единицу объема между фазой и стенкой канала, Н⋅м

П – смоченный периметр канала, м

θ - угол наклона канала к горизонтали

τ - временной шаг, с

ω - объем ячейки сетки, м³

ω_nom - номинальная частота вращения, с

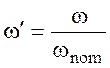 - безразмерная угловая скорость насоса

нижние индексы

f – параметры жидкой фазы

g – параметры газовой фазы

i – параметры на межфазной границе

k – идентификатор фазы (f, g)

n – параметры неконденсируемых газов

s – параметры в состоянии насыщения

w – параметры на стенке

v – параметры пара

верхние индексы

n – значения величин на верхнем временном слое.

4.2 Аппроксимация модели течения теплоносителя

              Система уравнений (2.1-2.7), описывающих термогидравлику двухфазной среды с примесью неконденсирующегося газа представляет собой систему 7 дифференциальных уравнений в частных производных с алгебраическими замыкающими соотношениями. Для численного решения в качестве основных независимых переменных выбраны следующие величины: .

4.2.1 Аппроксимация по времени

              Для аппроксимации уравнений течения теплоносителя по времени используется разностная схема, в основу которой положена схема [ 13 ]:

              ;

              ;

;

;

;

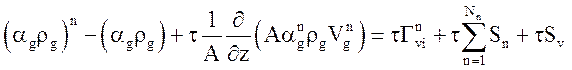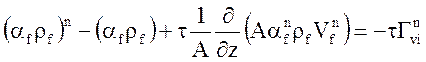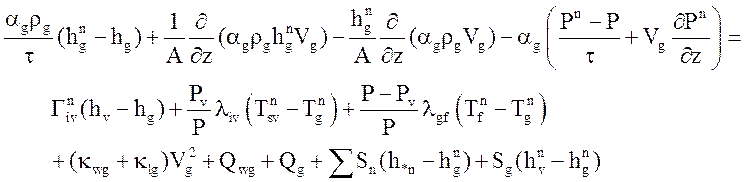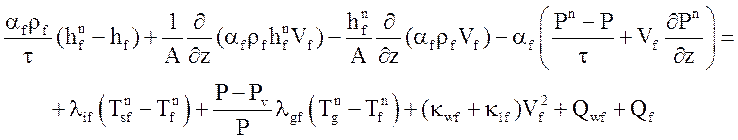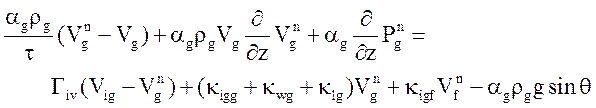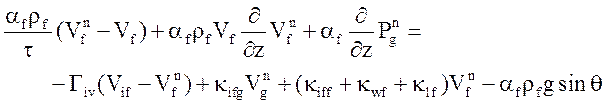
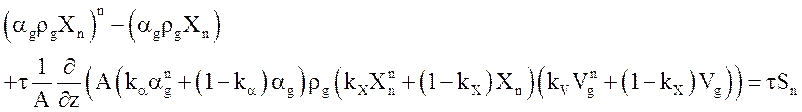
              Уравнения энтальпии преобразованы с учетом  определений (13) (14).

              Коэффициенты k_α, k_X, k_V в уравнениях переноса газов дают возможность использовать явную (0), неявную (1) или центрированную по времени (0.5) аппроксимацию соответствующих величин  в конвективном члене.

              Для численного решения система линеаризуется по времени. Нелинейные члены под знаком дивергенции в уравнениях неразрывности  линеаризуются следующим образом

.

              Интенсивность массообмена на верхнем слое, представляется как:

,

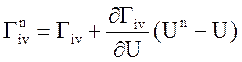где  вектор-функция независимых переменных.

              Плотности и температуры (зависимые величины) на верхнем временном слое так же определяются через независимые переменные:

              ;                                                              

              ;                                                              

              ;                                                                              

              ;                             

                                           .

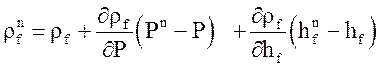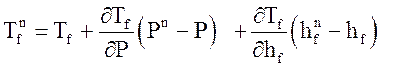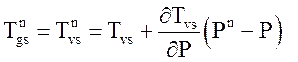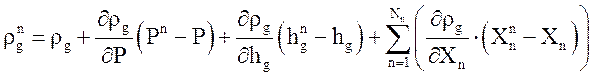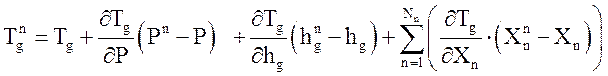              В этих соотношениях  плотности, температуры и их производные определяются из уравнений состояния воды и пара.

              Для определения ρ_g, T_g, ρ_v, P_v и их производных, через P, h_g и X_n используется система уравнений (1)-(5). Алгоритм расчета описан в разделе 3.3.

              При отсутствии неконденсирующегося газа

                                                                                     

                                                                    

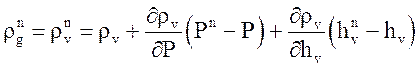
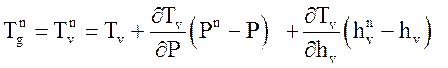
              Уравнения неразрывности для неконденсирующихся газов после линеаризации:

.

4.2.2 Пространственная аппроксимация

4.2.2.1  Разностная сетка

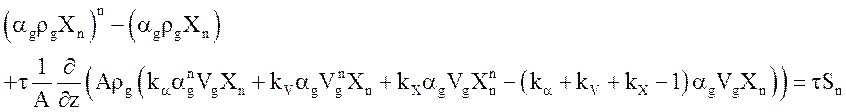              В качестве примера разностной сетки РАТЕГ04 на Рис. 3.1 изображен участок канала с тепловым элементом и обозначена расчетная сетка в канале и ТЭ. Границы ячеек сетки обозначены точечной линией. Наружная поверхность канала в пределах ячейки сетки аппроксимируется конической поверхностью (на Рис. 3.1 показано пунктиром). В РАТЕГ04 скорости фаз V_g, V_f в канале и температура в ТЭ определены в узлах сетки (помечены крестиком и полуцелым индексом), а остальные величины − в ячейках сетки. За положительное направление скорости выбрано направление, в котором нумерация ячеек сетки возрастает.

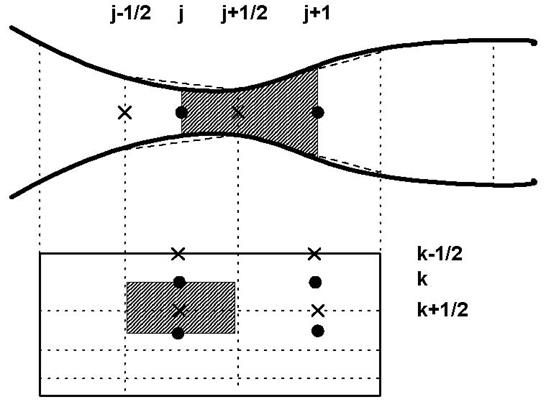
Рис. 3.1 Схема расчетной сетки в канале и тепловом элементе

              Расчетная сетка вдоль теплового элемента совпадает с сеткой соответствующего канала. Выбор радиальной сетки в ТЭ зависит от того, какое приближение используется для теплопроводности: одномерное или двумерное. При использовании одномерного приближения радиальная сетка может быть своя для каждого сечения. В двумерном случае радиальная сетка должна быть едина для ТЭ.

4.2.2.2  Аппроксимация в неразветвленных каналах

              Пространственная аппроксимация уравнений неразрывности и энергии строится путем интегрирования их по объемам ячеек сетки с ‘донорным’ определением потоков. В результате разностные уравнения имеют следующий вид.

              Уравнение неразрывности газовой фазы

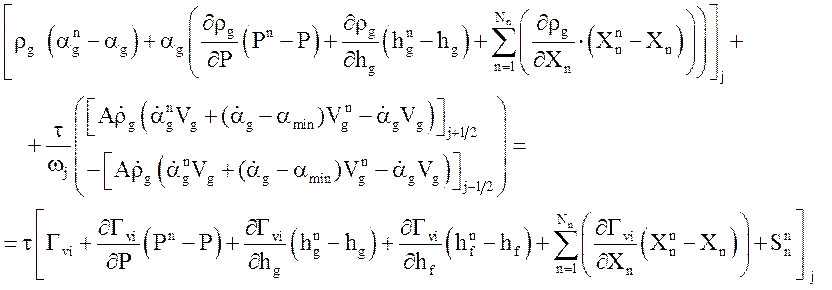
              Уравнение неразрывности жидкой фазы

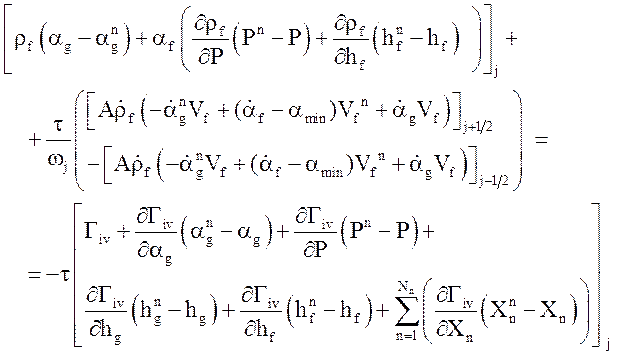       (34)

              Для упрощения аппроксимации, в уравнениях энергии адвективный член в полной производной по времени от давления заменяется следующим образом .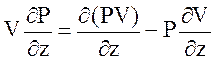

              Уравнение энергии газовой фазы

             

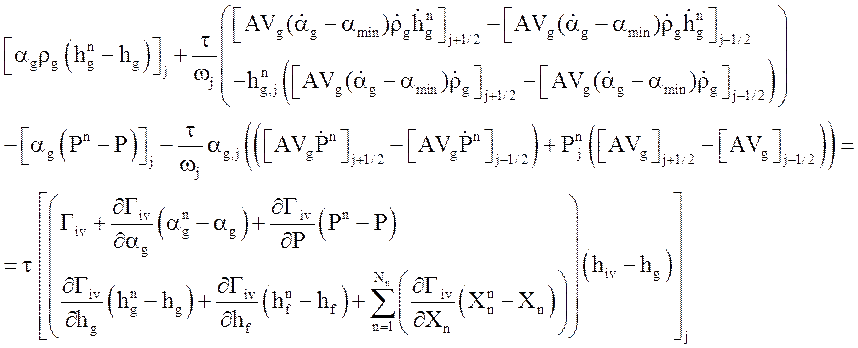
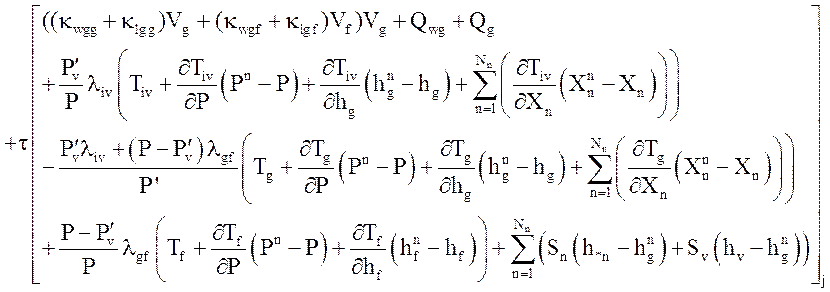
              Уравнение энергии жидкой фазы

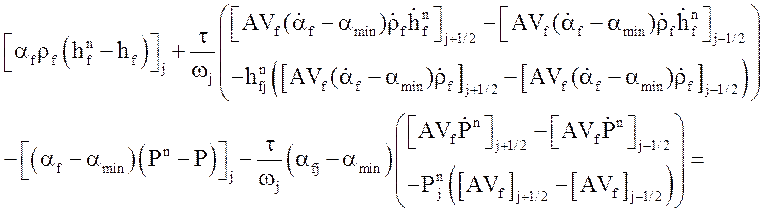
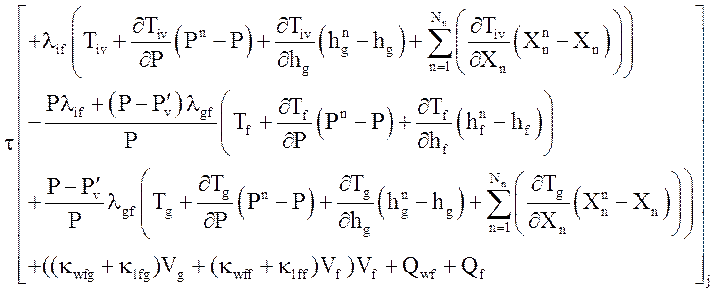
              Уравнения неразрывности неконденсируемых газов

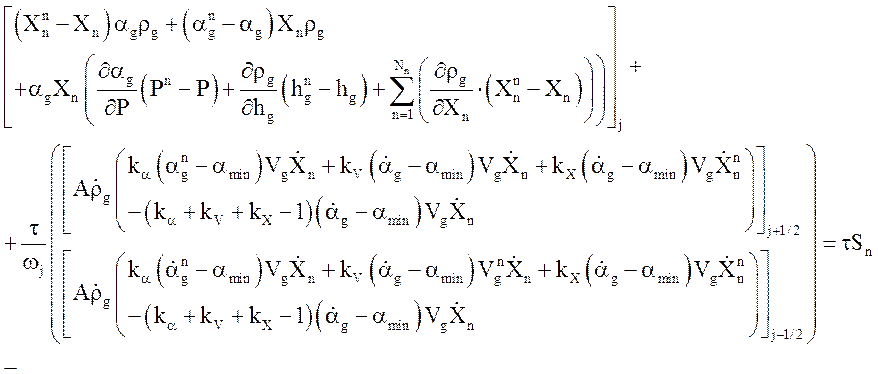
              Значения скалярных величин на границах ячеек:

,

.

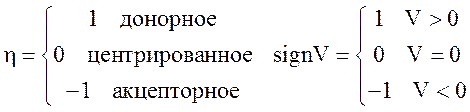              Дивергентная аппроксимация потоков энтальпии и давления в узлах с большими градиентами объемной концентрации фаз приводит к появлению нефизичных экстремумов в этих величинах. Что бы избежать этого в таких узлах (|α_gj - α_gj+1| ≥ 0.97) используется недивергентная аппроксимация конвективных членов

,

.

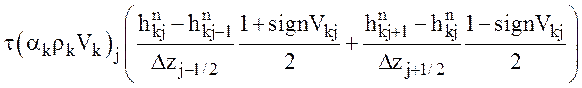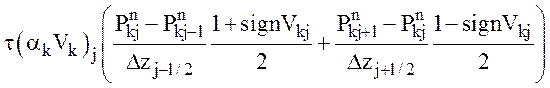              Для упрощения аппроксимации уравнения движения используются в недивергентной форме. Пространственные производные в уравнениях движения аппроксимируются «вверх по потоку»: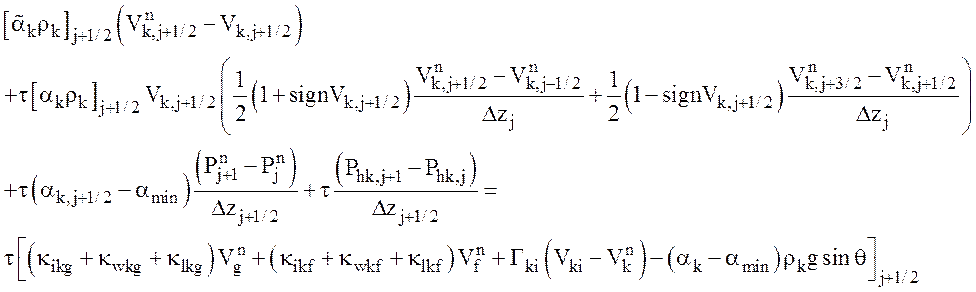              Корректировка объемной концентрации в узле расчетной сетки вводится для улучшения обусловленности матрицы системы линейных уравнений при малых концентрациях фазы: .