Учебный пакет программ “sFlow” для компьютерного моделирования процессов гидродинамики и тепломассообмена, страница 5

4. Для тепловых задач находится градиент энтальпии (17) и эффективная теплопроводность (16). Корректируются коэффициенты конечно-разностной (конечно-объемной) аппроксимации уравнения теплопереноса в пристеночном контрольном объеме.

5. Определяем правую часть уравнения для энергии турбулентных пульсаций и пристеночное значение для диссипации (удельной диссипации) (27-28 или 29). Корректируются коэффициенты конечно-разностной (конечно-объемной) аппроксимации транспортных уравнений для k и e (w) в пристеночном контрольном объеме.

3. Дискретизация

3.1. Сетки и контрольные объемы

Для решения заложенных в алгоритм пакета уравнений используется широко известный метод контрольного объема. Суть которого заключается в разбиении расчетной области на контрольные объемы (рисунок 3.1.1.) и интегрировании исходных уравнений сохранения  по каждому контрольному объему для получения конечно разностных соотношении.  Свойства метода достаточно подробно описаны в литературе [29],[33].   

В пакете “sFlow” используются одноблочные структурированные криволинейные сетки с исключаемыми областями.

Приведем здесь для примера несколько расчетных сеток.

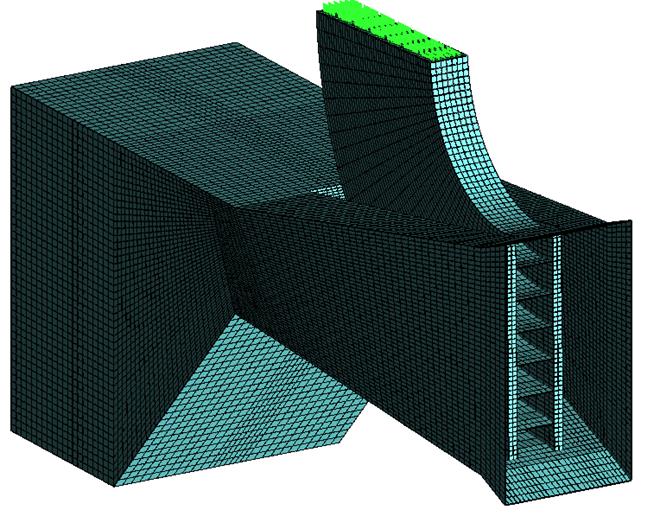
Прямоточная горелка

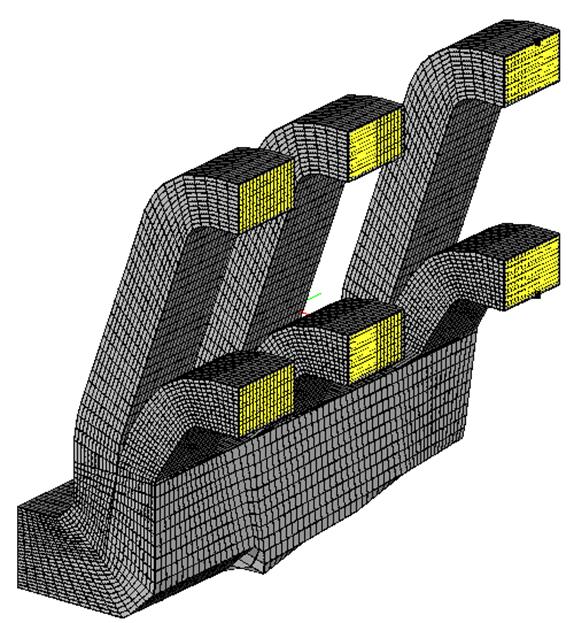
Газоход

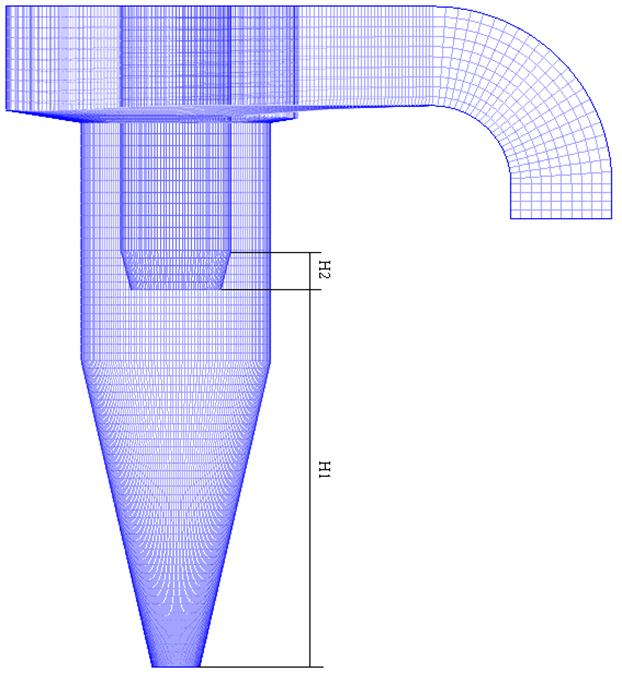
Скруббер

 3.2. Метод контрольного объема на примере обобщенного уравнения переноса

3.2.1. Дискретизация обобщенного уравнения   в декартовой системе координат

Дифференциальные уравнения сохранения можно представить в виде одного уравнения для обобщенной переменной F:

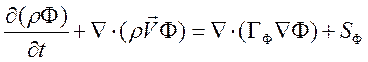                                                           (3.2.1)

Задавая надлежащим образом F,  Г_ф и источник S_F (табл.1), можно получить любое из упомянутых выше дифференциальных уравнений.

Запись уравнений в обобщенном виде удобна в том отношении, что какой-либо разработанный метод решения для этого уравнения может быть применен для многих уравнений подобной структуры, но различного физического наполнения.

Таблица 3.2.1.

Ф	Гф	Sф
1	0	0
u	meff
v	meff
w	meff
h	meff/sh	Sh
Ym	meff/sY	Sm
k	meff/sk	G-re
e	meff/se

Решение уравнения (3.2.1) будем производить методом контрольного объема. Интегрируем уравнение (3.2.1) по контрольному объему, в центре которого лежит узел с индексами (i,j,k).

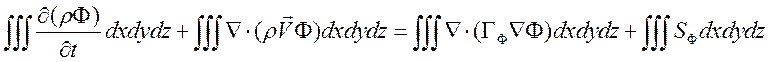          (3.2.2)         

Используя формулу Гаусса-Остроградского, переходим от объемных интегралов к поверхностным  и получаем:

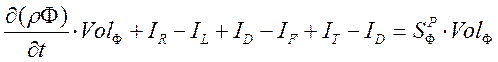                                                  (3.2.3)

где -объем контрольного объема, -среднее в ячейке значение источникового члена, -суммарный конвективно-диффузионный поток через соответствующую грань к.о..

Описание заложенных в расчетный алгоритм пакета схем аппроксимации потока удобно проводить на одномерном шаблоне (например, в направлении оси OX), дискретизация уравнения (3.2.1) в остальных направлениях осуществляется аналогично.

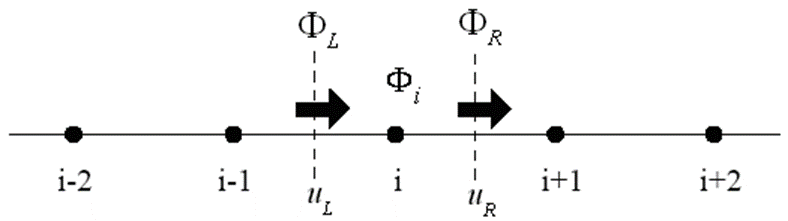
Рисунок 3.2.1 Одномерный контрольный объем.

Величина суммарного потока для правой грани контрольного объема определяется как:

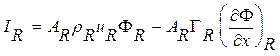                                                                                 (3.2.4)

здесь -площадь грани , ,,-значения плотности, скорости, коэффициента диффузии на грани к.о., которые находятся при помощи  интерполяции из соседних узлов

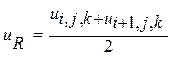
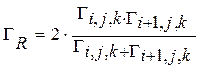                                                                    (3.2.5)

3.2.1.1. Аппроксимация диффузионного потока

Аппроксимация диффузионной части суммарного потока

производится при помощи центрально разностной схемы второго порядка точности.

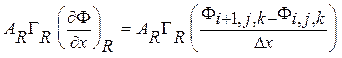                                                                         (3.2.1)

3.2.1.2. Схемы аппроксимации конвективного потока

Задача нахождения конвективной части суммарного потока  сводится к отысканию значений искомой функции  на гранях контрольного объема по известным значения ее в узлах сетки. Выбор способа интерполяции величины между узлами расчетной сетки определяет свойства полученной при этом разностной схемы. В  пакете “sFlow” реализованы следующие схемы аппроксимации.

Гибридная схема (Hybrid)

Чтобы повысить точность UDS схемы без потери ею устойчивости, было предложено  использовать гибридную схему, сочетающую противопоточную и центрально-разностную схемы.

Которую можно записать так:

                             

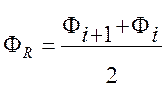
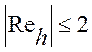                                                                          (3.3.1)

                   

где 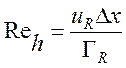 - сеточное число Рейнольдса.

Данная схема устойчива при любых числа Рейнольдса, в то же

время при расчете сложных циркуляционных течений,  когда отсутствует преобладающее направление движения жидкости, гибридная схема вызывает большие вычислительные ошибки при нахождении локальных характеристик течения.

При построении схем высокого порядка для повышения устойчивости в “sFlow” используется следующий широко известный подход

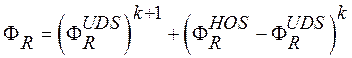                                                                       (3.3.2)

где и  - величины искомой функции Ф полученные при помощи схемы UDS и какой-либо схемы более высокого порядка, k-номер итерации.

При этом в качестве основной  схемы берется схема (UDS), которая дополняется некоторой корректирующей добавкой, которая явно вносится в источниковый член с предыдущей итерации. Полученная таким образом схема с точки зрения сходимости почти не уступает гибридной схеме, однако существенно превосходит ее по точности. Исходя из этого, все  представленные ниже схемы записаны в виде, в котором явно выделена схема UDS и корректирующая добавка.

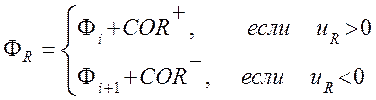                                                                    (3.3.3)

Линейная противопоточная схема второго порядка (SCHY)

В данной схеме величина  находится при помощи линейной интерполяции по  двум прилегающим к грани R узлам лежащим выше по потоку.

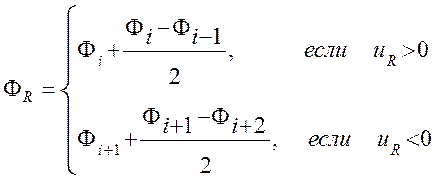                                                           (3.3.4)

Квадратичная противопоточная схема (QUICKM)