где коэффициент пропорциональности Е носит название модуля упругости. Физический смысл Е становится понятным, если положить e=1, т.е. когда Dх = х0 (рис.2.1.2,б), то Е = s - модуль упругости (или модуль Юнга) численно равен механическим напряжениям, при которых длина образца увеличивается вдвое. Только некоторые полимерные материалы и каучук выдерживают такие деформации, не разрушаясь. Следует заметить, что из-за различий межатомных расстояний в элементарных ячейках (см. ячейки Бравэ в ч.1, табл.1.1.5) жесткость связей b и модуль упругости различны в разных направлениях монокристаллов. В общем случае эти коэффициенты также образуют тензор, некоторая анизотропия наблюдается и в слоистых структурах. Но применительно к поликристаллическим материалам с равноосными зернами, к спеченным, литым и горячепрессованным материалам, к недеформированному и отожженному стеклу и другим аморфным материалам обычно применяют понятие "изотропный модуль упругости Е", значения которого и приведены для ряда материалов в табл. 2.1.1.
Применительно к касательным напряжениям и сдвиговым деформациям закон Гука записывают в форме
t = G×g, (2.1.10)
где G - модуль сдвига материала (модуль Пуассона).
Между значениями модулей Е и G существует аналитическая связь:
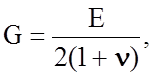(2.1.11)
где n
- коэффициент Пуассона,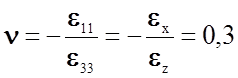 
(для
многих твердых тел) - отношение поперечного сжатия к продольному растяжению
одноосно деформируемого вдоль оси Z образца (рис.2.1.2,б). Для монокристаллических
тел величина G зависит от направления деформирования и
вида напряженного состояния, но к поликристаллам во многих случаях также применимо
понятие "изотропный модуль сдвига" (см. табл.2.1.1).
В практике расчетов свойств твердых тел в пределах их упругого поведения находит применение еще одна макроскопическая характеристика - объемный модуль упругости, или модуль всестороннего сжатия (растяжения), K. Эта характеристика может быть определена из ее связи с модулями Е и G:
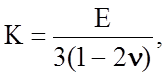(2.1.12)
или, используя соотношение (2.1.11),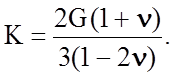 
Точный вывод соотношений (2.1.11), (2.1.12) и определение величины n для различных видов напряженного состояния осуществлены в рамках теории упругости в курсе сопротивления материалов.
В практике исследования механических свойств материалов установлено, что пластическая деформация и разрушение сдвигом происходят в основном под действием касательных напряжений. Нормальные напряжения играют определяющую роль в разрушении тел отрывом. При нагружении поликристаллического или аморфного образца комбинированное воздействие нормальных и касательных воздействий способствует развитию пластической деформации скольжением в некоторых предпочтительных плоскостях.
На рис. 2.1.1. выделена некоторая плоскость 
, нормаль к которой образует угол a с направлением растяжения. Если
действующую силу F разложить на нормальную Fн
и тангенциальную Ft составляющие, то можно определить
напряжения (s = F/ и t
= Ft/ , нормальные и касательные к плоскости
.
Поскольку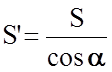 
, а Ft = F×sina, то 
=
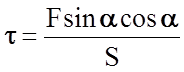= s sina×cosa и достигают своего максимума tm при a = 45°. В случае нагружения монокристаллических образцов, где скольжение может происходить лишь по некоторым направлениям наиболее плотной упаковки атомов, пластическая деформация начинается в том случае, когда касательные напряжения t превышают некоторое критическое значение
tk = s sina×cosb , (2.1.13)
характерное для данного материала и данной системы скольжения.
Этот закон п о с т о я н с т в а критического скалывающего напряжения экспериментально сформулирован Е.Шмидом и В.Боасом (b - угол между направлением скольжения и максимумом касательных напряжений).
В
гранецентрированной кубической решетке скольжение развивается по плоскостям
{111} в направлениях <110>, всего таких систем скольжения 12 и потому
кристаллы с ГЦК-решеткой очень пластичны. В кристаллах с объемно-центрированной
решеткой основными плоскостями скольжения являются плоскости {110}, а
направлениями - <111> и здесь также 12 возможных систем легкого
скольжения. В гексагональных решетках плоскостями скольжения служат плоскости
базиса {0001}, в которых имеется три равноправных направления скольжения 
Деформация скольжением легко происходит в веществах с металлической и ионной связями, но затруднена в кристаллах с направленной ковалентной связью, которые по этой причине являются очень твердыми, но хрупкими.
Основным механизмом пластической деформации моно- и поликристаллов, а также аморфных тел является сдвигообразование. Альтернативным процессом в условиях стесненности скольжения и пониженных температур является механическое двойникование. Трансформация кристаллической решетки при этих видах пластической деформации описывалась выше (ч.1).
Грубо оценим величину касательного напряжения, необходимого для осуществления гомогенного сдвига цепочки атомов на один параметр решетки (рис.2.1.4). Примем, что напряжения, необходимые для смещения пары атомов из одного равновесного положения в другое, изменяются с расстоянием по синусоидальному закону. Сопротивление цепочки деформации сдвига, следуя Френкелю, опишем уравнением
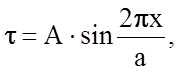(2.1.14)
где х - смещение в направлении сдвига, а - параметр решетки в направлении сдвига, А – некоторая постоянная, величину которой можно оценить.
Будем считать смещение настолько малым, чтобы выполнялось соотношение
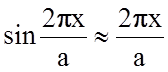и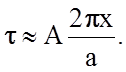 
(2.1.15)
Для такого сдвига справедлив закон Гука
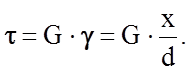(2.1.16)
Тогда из соотношений (2.2.15) и (2.1.16)
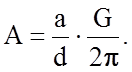(2.1.17)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.