Преобразование V → w является нелинейным, но оно близко к линейному при небольших w. Частота среза Vc аналогового фильтра соответствует частоте среза wc цифрового фильтра. По значениям Vc и wc можно вычислить постоянную k.
Если аналоговый фильтр нормализован и 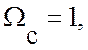 то
то 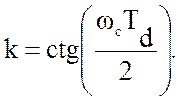
При этом 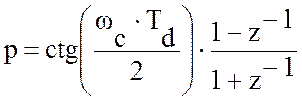 [1].
[1].
При билинейном преобразовании левая половина s-плоскости отображается внутрь единичной окружности в z-плоскости, поэтому синтез по устойчивому прототипу даст гарантированно устойчивый дискретный фильтр
[3].
3.1.Получение спецификации АФ на основе спецификации ЦФ;
3.2. Проектирование аналогового нормированного фильтра (прототипа)
3.3. Трансформация АФ в ЦФ
Спецификация ЦФ:
Fp=10000; %Гц, граничная частота полосы пропускания
Fs=11000; % Гц, граничная частота полосы задерживания
Ft=50000; % Гц, частота дискретизации
Rp=1; % Дб, неравномерность передачи в полосе пропускания
Rs=60; % Дб, минимальное ослабление в полосе задерживания
Tt=1/Ft; % сек, период дискретизации
Вычисление нормированных частот:
wp=2*pi*Fp/Ft % рад/отсчет, нормированная частота среза
ws=2*pi*Fs/Ft % рад/отсчет, нормированная граничная частота полосы задерживания
wp = 1.2566 рад/отсчет
ws = 1.3823 рад/отсчет
Определение
граничных частот по АФ по 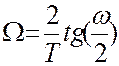 :
:
Ws=2*Ft*tan(ws/2) % рад/с
Wp=2*Ft*tan(wp/2) % рад/с
Ws = 8.2727e+004 рад/с
Wp =7.2654e+004 рад/с
Проектирование аналогового фильтра будем осуществлять на основе нормированного ФНЧ (НФНЧ).
Определение граничной частоты полосы задерживания НФНЧ:
Omega_s=Ws/Wp
Omega_s = 1.1386
Параметры НФНЧ: Vp=1, Vs=1.1386, Amax=Rp=1дБ, Amin=Rs=60дБ.
Вычислим минимальный порядок аналогового прототипа, необходимый для выполнения заданных требований, используя функцию cheb2ord()
[n,Wn]=cheb2ord(1, Omega_s, Rp, Rs,'s')
n = 16
Wn = 1.1368
Определение коэффициентов передаточной функции НФНЧ поcheby2().
[b,a]=cheby2(N, Rs, Wn, ’s’) вычисляет коэффициенты числителя и знаменателя передаточной функции аналогового фильтра H(s) Чебышева 2-о типа порядка N с частотой среза Wn и минимально допустимыми отклонениями в полосе задерживания Rs дБ
[b,a]=cheby2(n,Rs,Wn,'s');
Преобразование НФНЧ в ФНЧ производится с помощью функции lp2lp().
В нее передаются коэффициенты полиномов числителя и знаменателя функции передачи (b,a) НФНЧ и частота среза, а ею возвращаются коэффициенты аналогового ФНЧ (num и den).
[num,den]=lp2lp(b,a,Wp);
Для синтеза дискретных фильтров по произвольным аналоговым прототипам методом билинейного z - преобразования предназначена функция bilinear(). Num и den– коэффициенты полиномов числителя и знаменателя функции передачи аналогового прототипа, Ft – частота дискретизации в герцах [3].
[numd,dend]=bilinear(num,den,Ft)
numd =
0.0129 0.0565 0.1767 0.4090 0.7785 1.2495 1.7327 2.0989 2.2360
2.0989 1.7327 1.2495 0.7785 0.4090 0.1767 0.0565 0.0129
dend =
1.0000 -0.3335 3.1096 -0.0692 3.8851 0.9510 2.7700 1.2207 1.3186
0.6725 0.4253 0.1943 0.0831 0.0283 0.0077 0.0015 0.0002
Векторы numd и dend содержат коэффициенты числителя и знаменателя передаточной функции целевого фильтра.
Запишем уравнение проектируемого цифрового фильтра.
Передаточная функция БИХ - фильтра выражается дробно-рациональной функцией:
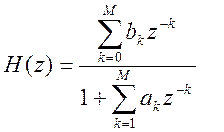
В общем виде цифровые БИХ - фильтры описываются линейным разностным уравнением с постоянными коэффициентами:
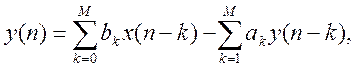
где x(n) – входной сигнал, y(n) – выходной сигнал, ak, bk – коэффициенты фильтра [1]. Используя выше приведенные коэффициенты передаточная функция фильтра:
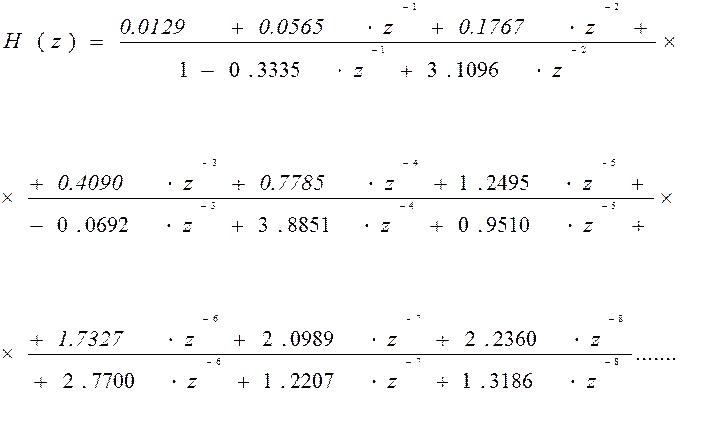
Отсюда уравнение проектируемого фильтра будет иметь вид:
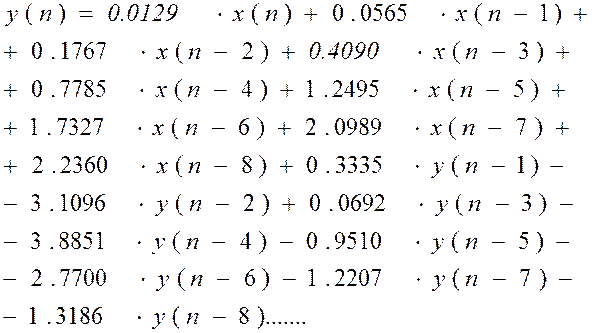
Для оценки устойчивости спроектированного цифрового фильтра, построим диаграмму нулей и полюсов:
zplane(numd,dend)
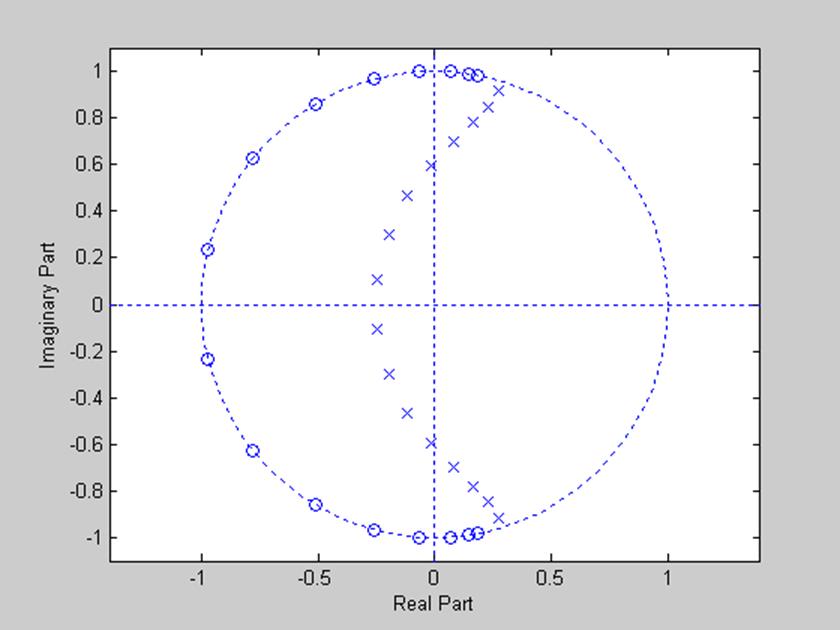
Рис.3. Диаграмма нулей и полюсов.
По условию устойчивости полюсы должны быть внутри единичной окружности на плоскости z. Из полученной диаграммы видно, что спроектированный фильтр является устойчивым.
Построим АЧХ и ЛАЧХ цифрового фильтра нижних частот Чебышева 2-го типа.
[H,f]=freqz(numd,dend,256,Ft);
subplot(2,1,1)
plot(f,abs(H)),grid
axis([0,20000,0,1.2])
title('Magnitude response')
xlabel('Frequency, Hz ')
subplot(2,1,2)
plot(f,20*log10(abs(H))),grid
axis([0,20000,-85,0.1])
title('Logarifmic magnitude response')
xlabel('Frequency, Hz ')
ylabel('Magnitude, dB ')
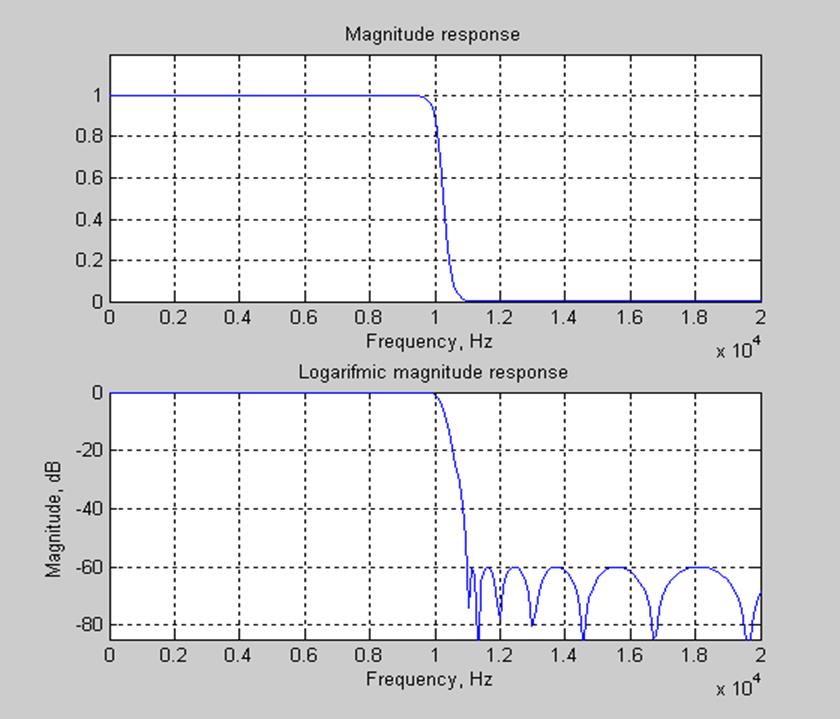
Рис.4 Графики АЧХ и ЛАЧХ цифрового ФНЧ Чебышева 2-го типа
При увеличении масштаба АЧХ (рис.5) можно убедиться в наличии равноволновых пульсаций в полосе задерживания спроектированного фильтра, что обусловлено его спецификой.
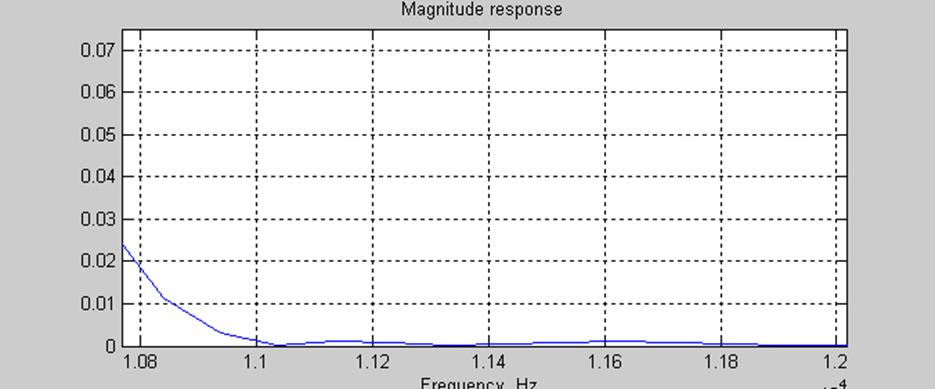
Рис.5. Полоса задерживания фильтра (увеличенный масштаб)
Построение ФЧХ спроектированного фильтра:
[H,f]=freqz(numd,dend,256,Ft);
figure (8)
subplot(2,1,1)
plot(f,angle(H)),grid
title('Phase response')
xlabel('Frequency, Hz')
ylabel('Phase, degrees')
axis([0,25000,-4,4])
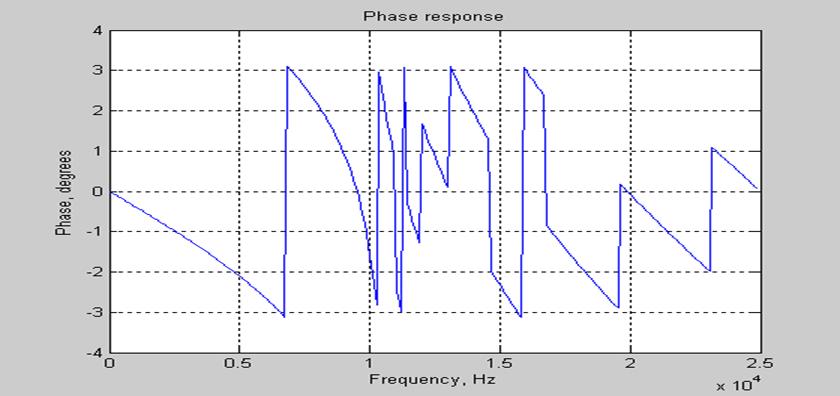
Рис.6 График ФЧХ цифрового ФНЧ Чебышева 2-го типа
По рис.6 видно, что ФЧХ данного фильтра нелинейная, так как данный фильтр с бесконечной импульсной характеристикой.
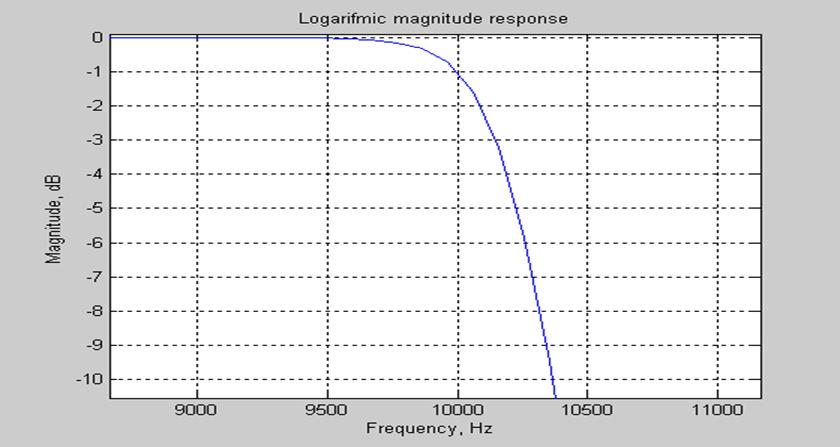
Рис.7. Граничная частота полосы пропускания (увеличенный масштаб ЛАЧХ).
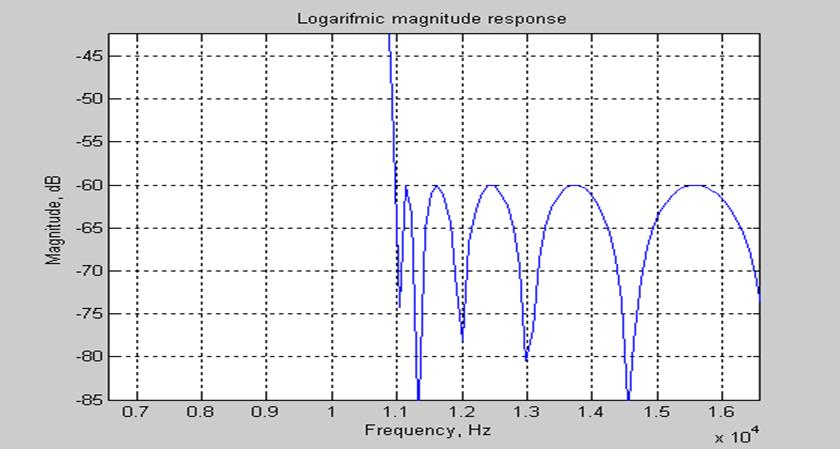
Рис.8. Граничная частота полосы задерживания (увеличенный масштаб ЛАЧХ).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.