Преобразование функции f(x)= exp(-(x+1)/x) численными методами, страница 3

Из проделанной выше работы следует, что при восьми итерациях метод с использованием сплайн-функций лучше всего интерполирует заданную функцию, что же касается МНК и МНК с применением ортогональных многочленов Чебышева, то предпочтительнее выглядит второй способ, т.к. погрешности ,получаемые при использовании данного алгоритма, намного меньше чем при использовании первого алгоритма.

4. Численные методы интегрирования

Определенный интеграл, посчитанный при помощи стандартной функции пакета MathCAD

4.1  Численное интерполирование с использованием сплайн-функций

Зададимся опорными точками

Производная функции в нулевой точке:

Точность данного результата соответствует заданной

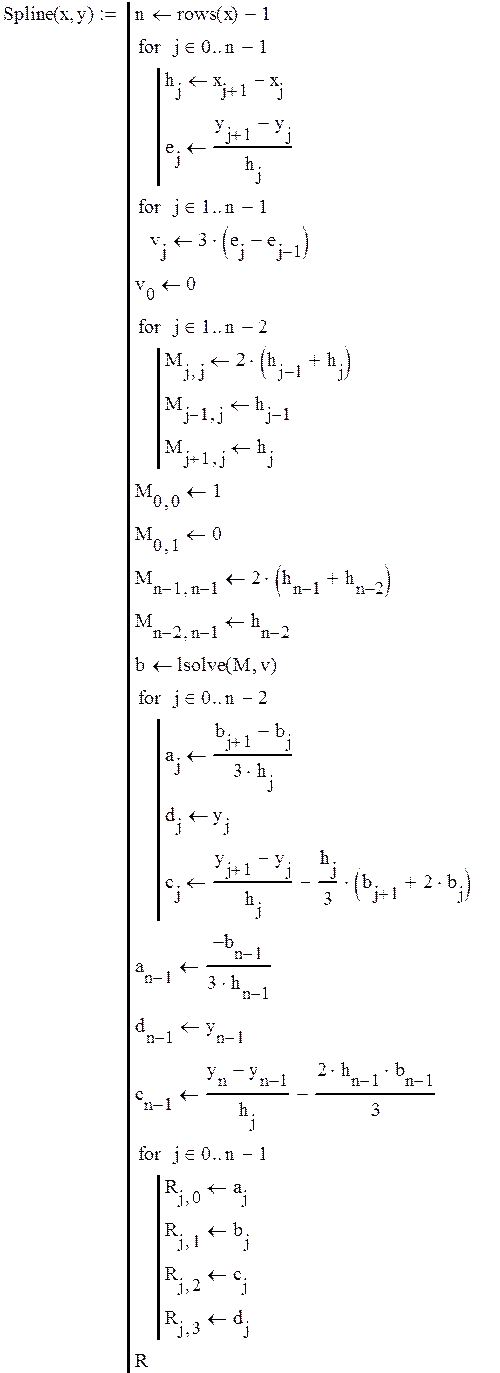
4.2   Метод трапеций

Т.к. абсолютная погрешность больше заданной, найдем ошибки

Нахождение ошибки ограничения

Абсолютная погрешность меньше заданной, данный результат нас устраивает.

4.3  Метод Симпсона

Точность полученного результата нас полностью устраивает, но все же найдем ошибки вычисления.

Как видно из сводной таблицы результатов при нахождении определенного интеграла функции f(x) методом Симпсона с 8 итерациями получился наиболее точный результат, с погрешностью меньшей заданной. Что же касается метода трапеций, то результат, получаемый при помощи данного метода, не устраивает нас, но  после вычисления  ошибки ограничения результат приближается к истинному. Нахождение определенного интеграла при помощи сплайн-функций при 8 интеракциях дает большую погрешность, что говорит о том , что данный метод требует большего числа разбиений

5. Нахождение значений производных функций численным методом

 

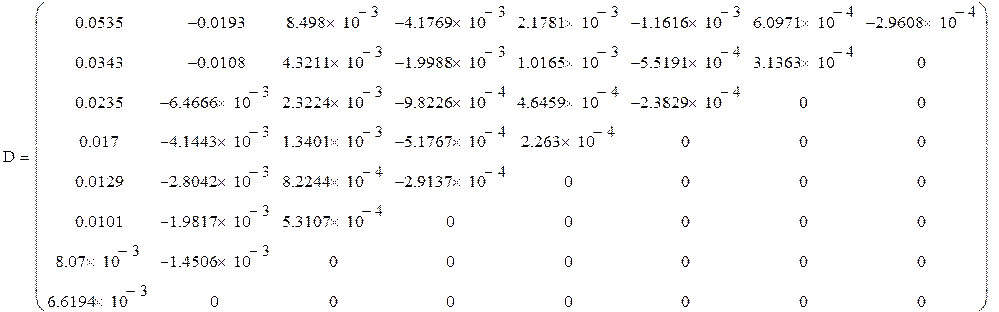Производная функции в точках X_i

Первые производные, полученные    Первые производные, полученные при

по методу Ньютона.                             помощи стандартной функции пакета MathCAD           

Вторая производная в толчках X_i

R_x – погрешность в точке x

Вторые производные, полученные    Вторые производные, полученные при

по методу Ньютона.                             помощи стандартной функции пакета MathCAD

Из полученных значений первой и второй производных по методу Ньютона следует, что данный метод достаточно точно считает производные в заданных точках с необходимой погрешностью.

6. Заключение

На практике в большинстве случаев найти точное решение возникшей математической задачи не удается. Это происходит главным образом не потому что мы не умеем этого сделать, а поскольку искомое решение обычно не выражается в привычных для нас элементарных или других известных функциях. Поэтому большое значение приобрели численные методы, то есть методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами. Решение, которое получено численным методом обычно является приближенным, то есть содержит некоторую погрешность. Даже если отсутствует погрешность во входных параметрах и при идеальном выполнении арифметических действий, все равно есть погрешность метода. В этом мы убедились, выполняя расчетно-графическую работу. Исследованию погрешности численных методов уделяется значительное внимание, и если можно определить, что погрешность меньше чем в других методах, то этот метод можно считать наиболее подходящим.

Для решения одной и той же задачи можно использовать несколько численных методов.

На мой взгляд, подходящим методом, где максимальная погрешность мала, в первом задаче является метод интерполирования с применением сплайн-функций. Во второй задаче – метод Симпсона, ну а метод Ньютона в третьей задачи позволяет найти результат с заданной точностью.

Использование литературы, приведенной ниже, помогло мне выполнить данную работу и  приобрести достаточно знаний для понимания данного курса.

       7.Литература

1. Методические указания к лабораторным работам по дисциплине “Вычислительная математика”.