Поиск среднего значения и стандартного отклонения результатов измерений. Поиск среднего значения и выборочных дисперсий, автокорреляционные функции и взаимную корреляционную функцию

Задачи 12

Примеры решения задач

1.  Десять независимых измерений напряжения представляют собой отсчеты гауссовского случайного сигнала и имеют значения:

207, 202, 184, 204, 206, 198, 197, 213, 191, 201  В.

Найдите среднее значение и стандартное отклонение результатов измерений.

Решение.

Среднее значение напряжения, т.е. оценка математического ожидания

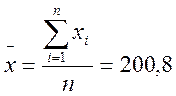   В.

Стандартное отклонение 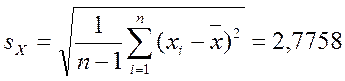    В

2.  Пусть рассматриваются два статистически независимых случайных сигнала X и  Y со средними значениями   и     и дисперсиями    и  . 

 Найти : а)  среднее значение произведения сигналов  

б)    дисперсию разности сигналов  .

Решение.

а)  Так как сигналы статистически независимы, то .

б) Дисперсия разности независимых сигналов   .

3.   Дискретный  случайный сигнал X(t_k ) представляет собой  гармонику со случайной равномерно распределенной в интервале   начальной фазой    (рис.1)

                                                                       Рис.1

Здесь      А- случайная амплитуда со средним значением  m_Aи средним квадратом  ,    Ф – независимая от амплитуды случайная фаза сигнала, равномерно распределенная в интервале  . 

 Является ли данный сигнал стационарным в широком смысле  и эргодическим?

Решение.

Представим  сигнал X(t_k )  в следующем виде:

.

Найдем математическое ожидание случайных величин  V₁   и  V₂

.

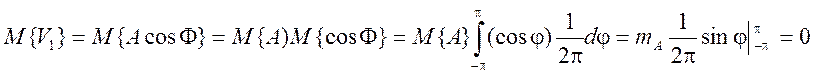Аналогично   , следовательно,  среднее значение случайного сигнала .

 В проведенных преобразованиях использовалось тождество  , так как величина А и Ф по условию задачи статистически независимы.

Определим, коррелированны или не коррелированны величины  V₁  и  V_2.  Для этого вычислим их корреляционный момент (корреляцию)

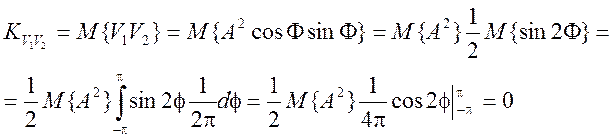
Следовательно, величины  V₁  и  V₂ не коррелированны.

Теперь найдем корреляционную функцию сигнала

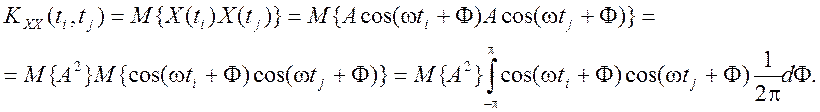
Для вычисления получившегося интеграла используем тригонометрическое тождество

.

Вычисляя интеграл с помощью этого преобразования, получаем  (рис.2)

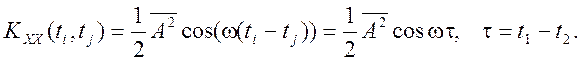
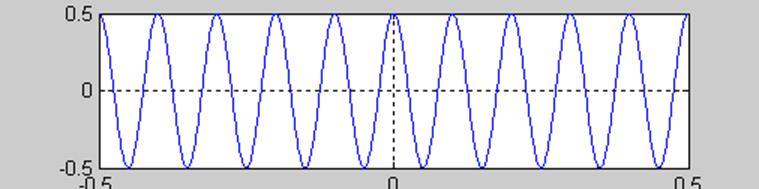
                                                                      Рис.2.

Таким образом, рассматриваемый случайный сигнал имеет нулевое (константное) математическое ожидание и корреляционную функцию, зависящую от разности 

аргументов,  т.е.  от сдвига сечений случайного сигнала. Значит, этот сигнал является стационарным случайным сигналом. Но он не является эргодическим, поскольку каждая реализация сигнала имеет различную начальную фазу и разные статистические характеристики при усреднении по времени.

4.   Заданы  двоичные дискретные сигналы   и .  Найдите их средние значения и выборочные дисперсии, автокорреляционные функции и взаимную корреляционную функцию.
Решение.
Средние значения  сигналов        .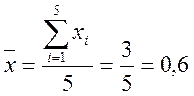

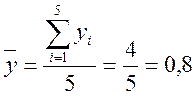Выборочные дисперсии (оценки дисперсии) сигналов 

,      .

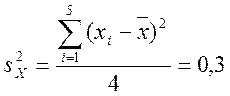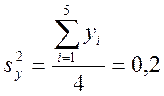Найдем автокорреляционные функции сигналов (смещенные оценки, деление на N)

    .  

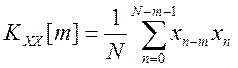
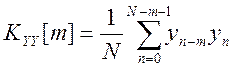При этом для наглядности будем иллюстрировать вычисления  графической схемой  

1	0	0	1	1
1	0	0	1	1

     

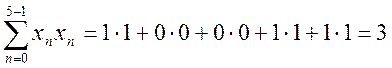
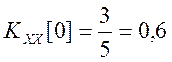
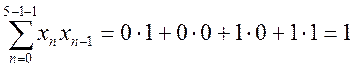
1	0	0	1	1
	1	0	0	1	1

                                     

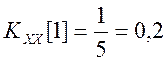
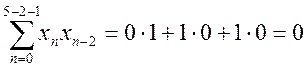
1	0	0	1	1
		1	0	0	1	1

                                                 

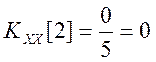
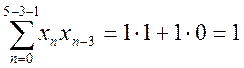
1	0	0	1	1
			1	0	0	1	1

                                              

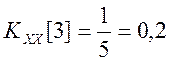
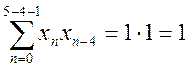
1	0	0	1	1
				1	0	0	1	1

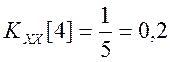
Значения  АКФ для отрицательных сдвигов  находим с помощью свойства четности  .

График    (рис. 3)

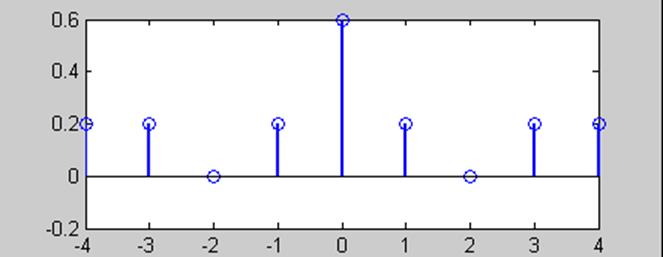
                                          Рис. 3.

Аналогично вычисляем  АКФ  ,  получим

Kyy[m] ={ 0.8000   0.4000   0.2000   0.4000   0.2000}

Определим взаимную корреляционную функцию (ВКФ) сигналов .   По определению

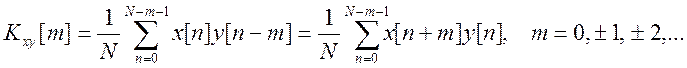
Вычислим последовательно значения ВКФ

1	0	0	1	1
1	1	0	1	1

        

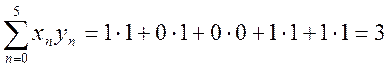
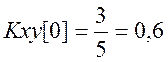
1	0	0	1	1
	1	1	0	1	1

         

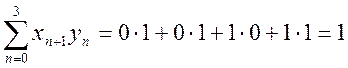
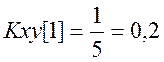
1	0	0	1	1
		1	1	0	1	1

                         

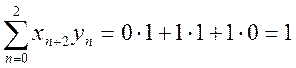
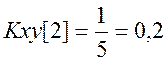
1	0	0	1	1
			1	1	0	1	1

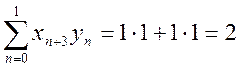
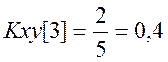
1	0	0	1	1
				1	1	0	1	1

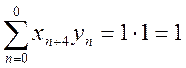
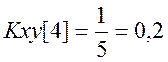
1	1	0	1	1
	1	0	0	1	1

 

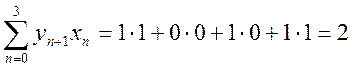
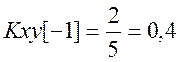
1	1		0		1		1
		1		0		0		1		1

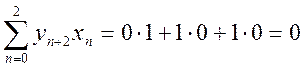
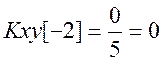
1	1	0	1	1
			1	0	0	1	1

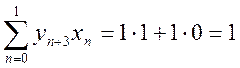
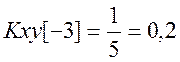
1	1	0	1	1
				1	0	0	1	1

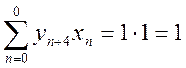
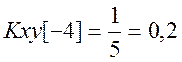
Таким образом,  ВКФ сигналов    .

Для  сопоставления вычислим и построим график ВКФ в среде Matlab

x=[1 0 0 1 1];

y=[1 1 0 1 1];

Kxy=xcorr(x,y,'biased')

Kxy =

    0.2000    0.2000    0.0000    0.4000    0.6000    0.2000    0.2000    0.4000    0.2000

m=-4:4;

stem(m,Kxy)

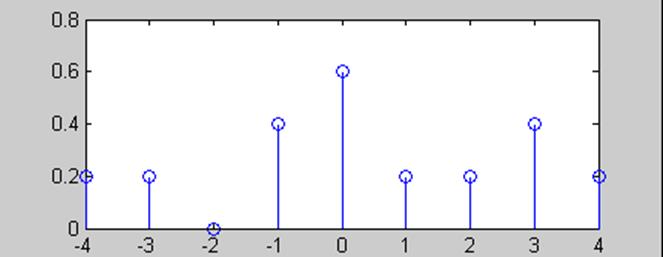
                                                                       Рис. 4

5.   Определите спектральную плотность мощности  сигнала   x = [1    0    0   1].
Решение.

Спектр  мощности сигнала и его автокорреляционная функция связаны преобразованием Фурье

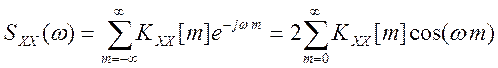
Для заданного сигнала  x

.

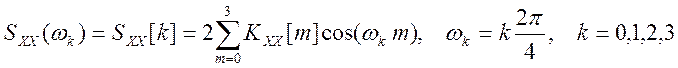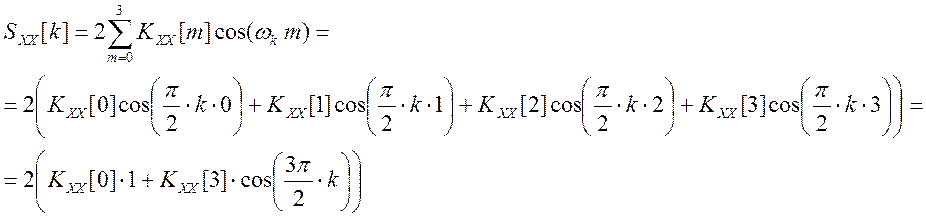
Найдем автокорреляционную функцию сигнала   x

1 0 0 1     1 0 0 1

1	0	0	1
1	0	0	1

1

0

0

1

1 0 0 1 1 0 0 1

1

0

0

1

Вычислим  по вышеприведенному выражению  значения  

Спектральная плотность мощности  P_XX(ω)  и спектр мощности S_XX(ω )  связаны через нормирующую константу  2 π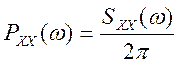           

График спектральной плотности мощности (рис. 5)

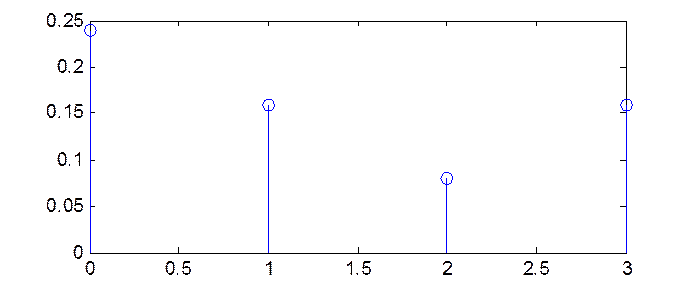
                                                                 Рис.  5.

6.   Найдите периодограммную  оценку  спектральной плотности мощности  (СПМ)  дискретного треугольного сигнала (рис.6)

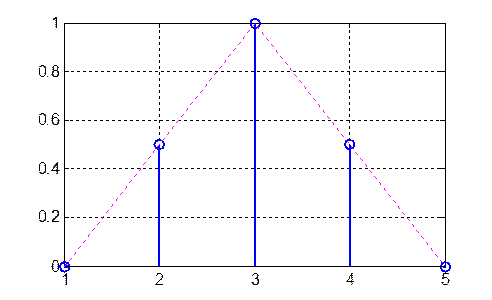
                                                                   Рис.6.

Решение.

x = {0     0,5      1       0,5      0 }

Периодограммная оценка  СПМ 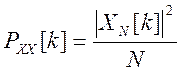  , где   - дискретное преобразование Фурье  (ДПФ) сигнала x,  N – число отсчетов сигнала.

Определим ДПФ заданного сигнала

.

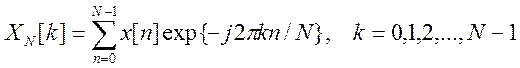Для  сигнала x

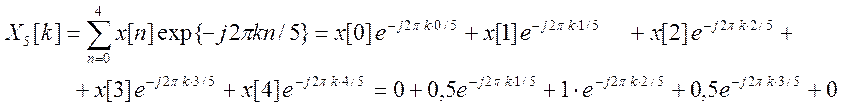
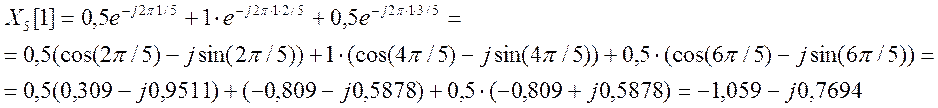Аналогичным образом вычисляются остальные  компоненты :

Вычисляем модули значений ДПФ:

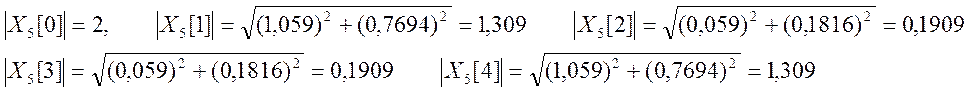
Теперь можем вычислить периодограммные  оценки СПМ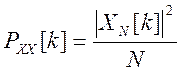 

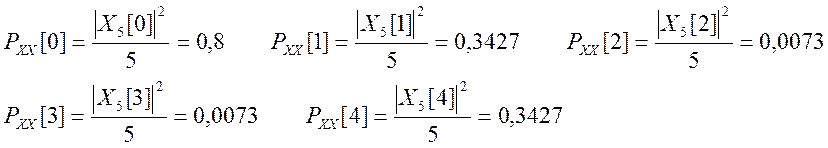
Мощность  сигнала можно вычислить, суммируя частотные компоненты СПМ

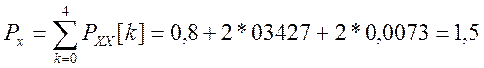
Для проверки вычислим мощность во временной области

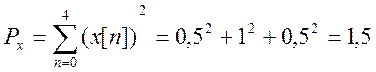
7.    Пусть  X[n] – некоррелированный белый шум с  автокорреляционной функцией   и спектральной плотностью мощности . Этот шум подается на вход идеального ФНЧ с угловой частотой среза  .  Определить мощность шума на выходе фильтра.
Решение.
Уравнение связи спектральной плотности мощности выходного и входного сигналов       . 
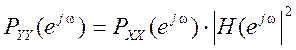 Для идеального ФНЧ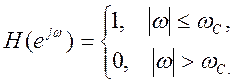    
Поэтому спектр мощности выходного шума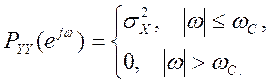   
Отсюда мощность выходного шума
.

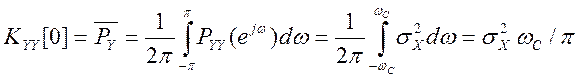8.  Дискретный белый шум с АКФ   поступает на вход суммирующего дискретного фильтра  с уравнением .   Найти спектральную плотность мощности  и среднюю мощность выходного сигнала фильтра.
Решение.

Спектральная плотность мощности входного сигнала – белого шума

.

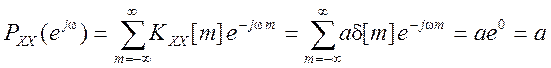Спектральная плотность мощности выходного сигнала фильтра

.

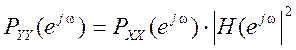Найдем АЧХ фильтра. Передаточная функция фильтра  .

 Частотная характеристика   .

  АЧХ фильтра      .

График АЧХ (рис.7)

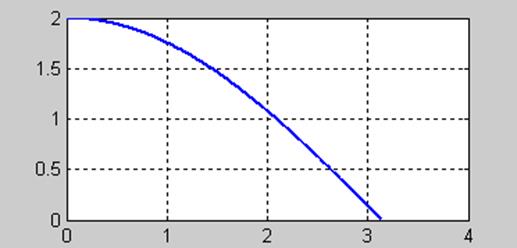
                                          Рис.7

 Следовательно, спектр  мощности  выхода фильтра 

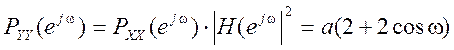   (рис.8)

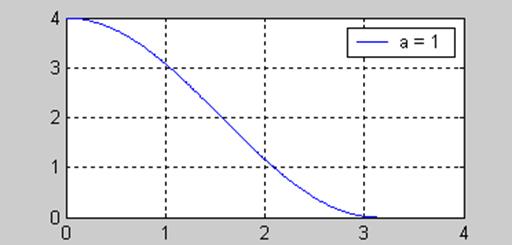
                                          Рис.8

Средняя мощность  выходного сигнала

.

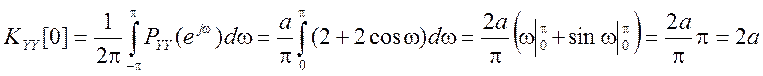Задачи для самостоятельного решения

1.   Случайный сигнал в каждом сечении представляет собой случайную величину с плотностью распределения вероятностей  . Запишите выражения для математического ожидания и дисперсии сигнала.

2.  Запишите и объясните выражение связи автокорреляционной функции и спектра мощности сигнала.

3.  АКФ стационарного дискретного сигнал имеет вид .  Найдите спектральную плотность мощности сигнала.

4.  Определите  периодограммную  оценку спектральной плотности мощности  (СПМ)  дискретного прямоугольного сигнала  x = {5    5    5    5    5}.

5.  На вход КИХ - фильтра с передаточной функцией    подается белый шум с АКФ 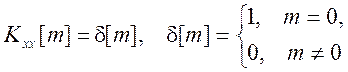 . Запишите выражение для АКФ выходного сигнала фильтра.

6.   На вход разностного КИХ – фильтра с уравнением   поступает случайный сигнал с АКФ 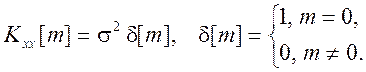 .   Определите среднюю мощность выходного сигнала фильтра.

7.  Белый шум с АКФ 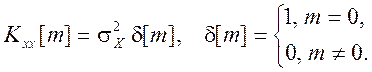   пропускается через  БИХ -  фильтр первого порядка с уравнением  .  Найдите спектральную плотность мощности и средний квадрат выходного сигнала фильтра.