Средняя мощность за период периодического сигнала s(t) конечна и равна
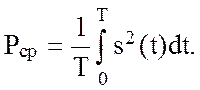 (2.55)
(2.55)
Представим сигнал рядом Фурье
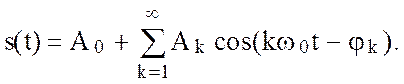
Заменим в интеграле (2.55) s(t) его разложением в ряд
Фурье, тогда 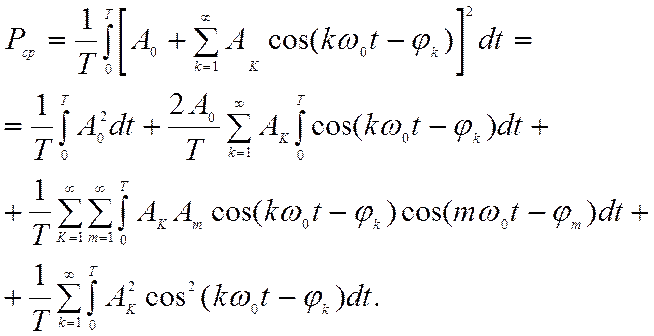 (2.56)
(2.56)
В этом выражении
|
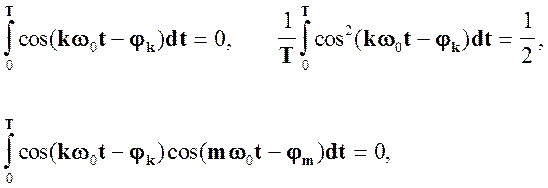
Таким образом, средняя мощность за период
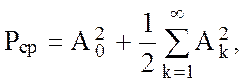 ` (2.57)
` (2.57)
т.е. равна средней мощности, выделяемой средним значением и гармониками сигнала. При этом средняя мощность не зависит от начальных фаз гармоник. Выражение (2.57) представляет собой частный случай рассмотренный в п.2.3 теоремы Парсеваля
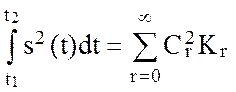 для гармонического ортогонального
базиса разложения.
для гармонического ортогонального
базиса разложения.
2.5. Непериодические сигналы.
2.5.1. Преобразование Фурье.
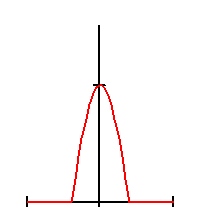
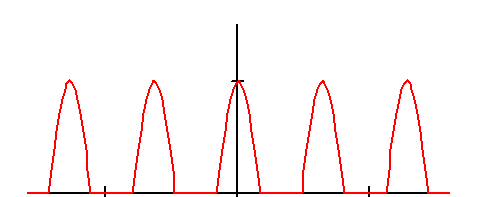
Непериодический сигнал s(t) определяется некоторой функцией, отличающейся от нуля в интервале (t1, t2) (рис. 2.9).
|
|
Рис. 2.9. Непериодический и периодически продолженный сигнал
Спектральное представление непериодических сигналов основывается на использовании преобразования Фурье, которое можно получить из ряда Фурье путем предельного перехода при Т ® ¥.
Пусть функция s(t) определена на интервале 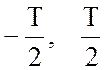 . Построим новую периодическую
функцию с периодом Т, при этом
. Построим новую периодическую
функцию с периодом Т, при этом
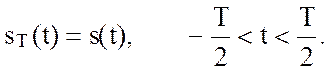 (2.58)
(2.58)
Ряд Фурье sТ(t) в комплексной форме имеет вид
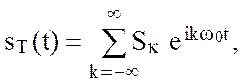 где
где 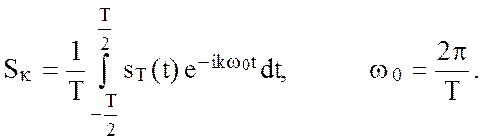
Введем новые обозначения wk = kw0,
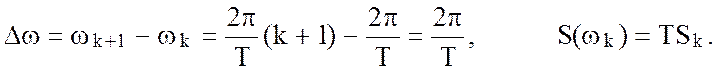
Тогда с учетом введенных обозначений
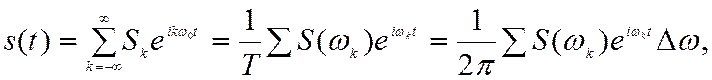 (2.59)
(2.59)
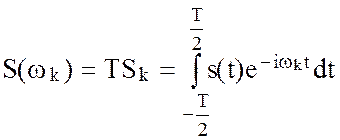 . (2.60)
. (2.60)
Перейдем к
пределу в выражениях (2.59) и (2.60) при T ® ¥. Если T ® ¥,
то 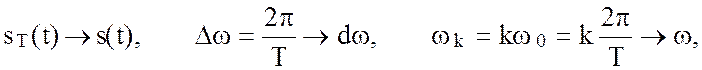 где w
-текущая частота.
где w
-текущая частота.
Предельные формы выражений (2.59) и (2.60) приобретают вид
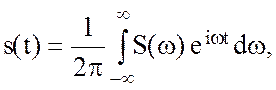 (2.61)
(2.61)
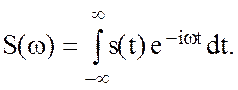 (2.62)
(2.62)
Выражения (2.61) и (2.62) представляют пару преобразований Фурье. Формула (2.62) является прямым преобразованием Фурье функции s(t), при этом комплексная функция S(w) называется спектральной плотностью для s(t). Соответственно формула (2.62) -обратное преобразование Фурье для S(w).
Связь между s(t) и S(w) через преобразования Фурье может быть представлена в символической форме
S(w) « s(t), (2.63)
которая означает, что s(t) и S(w) образуют пару преобразований Фурье в соответствии с формулами (2.61) и (2.62).
Другими словами, во временной области сигнал представляется функцией времени s(t), а в частотной - спектральной плотностью S(w).
Из формулы
прямого преобразования Фурье следует, что, если несобственный интеграл 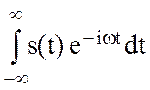 сходится, то спектральная плотность
для s(t) существует. Так как модуль
сходится, то спектральная плотность
для s(t) существует. Так как модуль 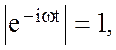 то
условие существования преобразования Фурье состоит в том, что
то
условие существования преобразования Фурье состоит в том, что 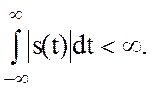 Более того, для сходимости
преобразования Фурье необходимо, что функция удовлетворяла условиям Дирихле [7],
[9], а именно:
Более того, для сходимости
преобразования Фурье необходимо, что функция удовлетворяла условиям Дирихле [7],
[9], а именно:
а) функция s(t) должна быть абсолютно интегрируемой, т.е.
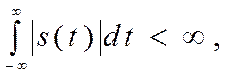 (2.64)
(2.64)
б) функция s(t) должна иметь конечное число максимумов и минимумов, а также конечное число разрывов на каждом конечном интервале.
В точке разрыва первого рода функции s(t) интеграл Фурье 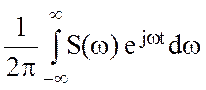 сходится к среднему арифметическому
пределов слева и справа [7].
сходится к среднему арифметическому
пределов слева и справа [7].
Условия Дирихле являются достаточными, но не необходимыми, это означает, что существуют функции, которые не удовлетворяют этим условиям, но имеют преобразование Фурье. На практике часто используется менее строгое условие существования преобразования Фурье, а именно
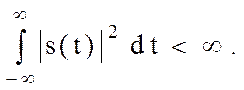 (2.65)
(2.65)
Это условие интегрируемости с квадратом означает конечность энергии сигнала s(t). Тем не менее ряд функций, широко применяемых в теории сигналов не удовлетворяет условиям Дирихле и условию интегрируемости с квадратом. Примером такой функции является, в частности, sin t, -¥ < t < ¥. Как будет далее показано, для таких функций можно определить спектральную плотность, используя аппарат обобщенных функций.
2.5.2. Спектр амплитуд и спектр фаз непериодического сигнала.
Во многих практических задачах, связанных с применением преобразования
Фурье, в качестве переменной интегрирования удобно выбрать не угловую частоту w, выражаемую в радианах в секунду, а
частоту в герцах (число периодов в секунду) 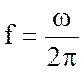 .
При этом выражение (2.61) преобразуется к виду
.
При этом выражение (2.61) преобразуется к виду
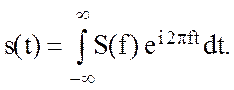 (2.66)
(2.66)
Соответственно изменяется прямое преобразование Фурье
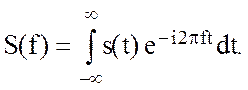 (2.67)
(2.67)
Сопоставим эту формулу с выражением (2.52) для k-го коэффициента Фурье
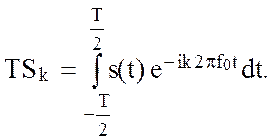 (2.68)
(2.68)
Видно, что функция S(fk) с точностью до константы при фиксированном k дает значение комплексной амплитуды k-ой гармоники разложения периодического сигнала s(t) в ряд Фурье.
Для непериодического сигнала частотный интервал Dw = 2p/T ® 0 при T ® ¥. Таким образом, интеграл
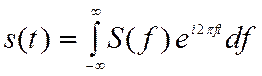 (2.69)
(2.69)
представляет
собой разложение в виде непрерывной суммы большого числа комплексных гармоник с
бесконечно малыми амплитудами. Элементарной составляющей сигнала здесь выступает
не отдельная гармоника ![]() , а приращение
, а приращение ![]() , где df - бесконечно
малое приращение частоты, а произведение S(f)df - бесконечно малая комплексная
амплитуда.
, где df - бесконечно
малое приращение частоты, а произведение S(f)df - бесконечно малая комплексная
амплитуда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.