Изучение сущности и моделей дискретизации (квантования по времени) сигналов и методов восстановления непрерывных сигналов по отсчетам

            МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

ЛАБОРАТОРНАЯ  РАБОТА  № 6

ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ СИГНАЛОВ

Группа: АИ-72                                                     Преподаватель: доц. Щетинин Ю.И.

Студент: Спитченко В.М.

Новосибирск

         2009

Цель работы:  изучение сущности и моделей дискретизации (квантования по времени) сигналов  и  методов восстановления непрерывных сигналов по отсчетам.

1.  Генерирование примера непрерывного и дискретного сигналов.

С помощью следующего script-файла сгенерируем пример дискретного сигнала  и непрерывного сигнала .

t = 0: 0.01 :5;

x = 2*log(t);

subplot(1,2,1);

plot(t,x);

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Непрерывный сигнал');

xlabel('t');

t1 = 0: 0.5: 5;

x1 =  2*log(t1);

subplot(1,2,2);

stem(t1,x1);

set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)

title('Дискретный сигнал');

xlabel('n');

Полученные результаты представлены на рис. 1.

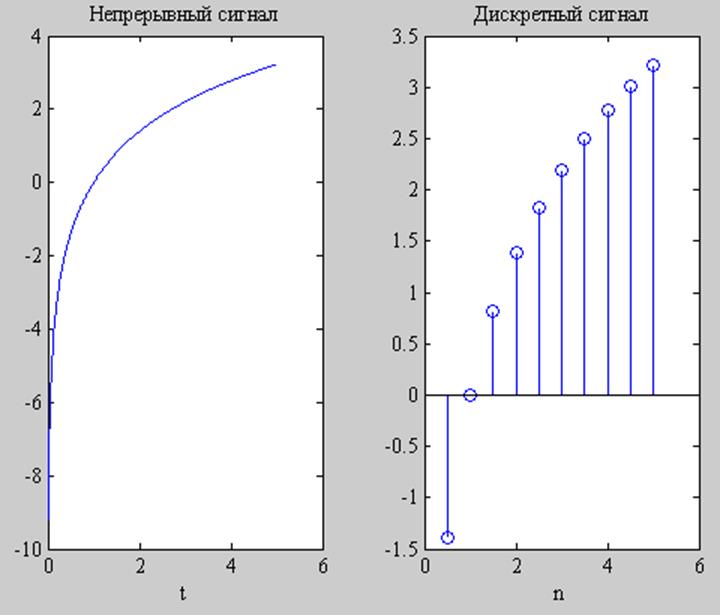
Рис. 1. Графики непрерывного и дискретного сигналов.

2.  Генерирование для непрерывного сигнала дискретных последовательностей с различной частотой отсчётов.

С помощью следующего script-файла для непрерывного сигнала   сгенерируем последовательности x[n]  при частоте  отсчетов 10000, 5000, 3000, 2000, 1500 Гц.

Fs = [10000 5000 3000 2000 1500];

t = 0:1/100000:0.005;

f = 1000;

x = cos(2*pi*f*t);

for n = 1:5,

    t1 = 0:(1/Fs(n)):0.005;

    x1 = cos(2*pi*f*t1);

    subplot(5, 1, n);

    plot(t1,x1, '-o', t,x);

    set(gca,'FontName','Arial Cyr', 'FontSize',10)

    title(['График гармоники при частоте отсчётов Fs =',num2str(Fs(n))]);

end

Полученные результаты представлены на рис. 2.

 

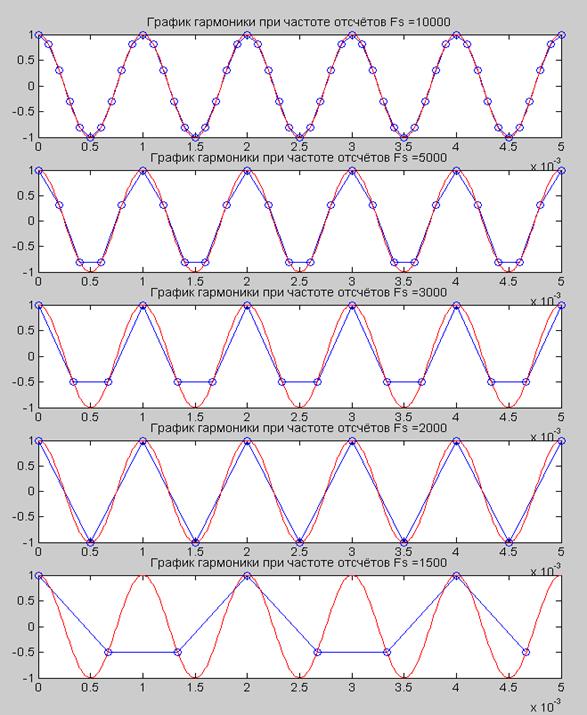Рис. 2. График непрерывного сигнала и

последовательностей x[n] при меняющейся частоте отсчётов Fs.

На рис.2 видим, что при увеличении частоты отсчётов точность приближения дискретного сигнала к непрерывному увеличивается.

По последнему графику нельзя определить период и амплитуду гармоники, это происходит при частоте 2000Гц, следовательно эта частота является предельной для данной гармоники.

----------- это всё вместо:

Форма дискретного сигнала близка к форме непрерывного при частоте отсчётов более   2000 Гц (т.е. при частоте в два раза превышающей частоту исходного косинусоидульного сигнала), значит, данная частота является предельной частотой отсчётов, достаточной для восстановления косинусоидульного сигнала.

Таким образом, получили результат, подтверждающий теорему отсчётов, которая утверждает, что если сигнал не имеет спектральных составляющих с частотами выше f_m, то он полностью определяется своими отсчетами в дискретные моменты времени через интервал отсчетов 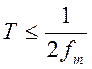  или с частотой  отсчетов . 

При частоте отсчётов 3000 и 5000 Гц непрерывный сигнал существенно расходится с дискретным, поэтому на практике предпочтительнее было бы выбирать частоту отсчётов выше предельной (например, 10000 Гц).

3.  Генерирование сигналов различной частоты при постоянной частоте отсчётов и сравнение их звучания.

С помощью следующего script-файла построим графики гармонических сигналов частотой 1000 и 6000 Гц, а также прослушаем звучание сигналов частотой 1000, 3000, 4000, 5000, 6000 Гц (частота отсчётов во всех случаях постоянна и равна 8192 Гц).

f = [1000 3000 4000 5000 6000];

for n = 1:5,

    [x, t] = harmonic(2*pi*f(n), 2*pi*8192, 1);

   [x1, t1] = harmonic(2*pi*f(n), 2*pi*30000, 1);

    figure(n)

    plot(t, x, '-o', t1, x1);

    sound(x)

    set(gca,'FontName','Arial Cyr', 'FontSize',10)

    title(['График гармоники частотой f =',num2str(f(n))]);

end

Полученные результаты представлены на рис.3 и рис.4.

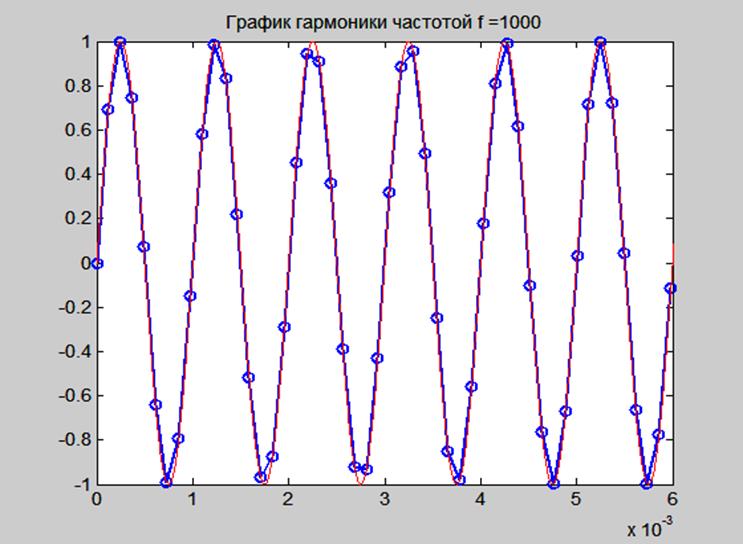
Рис. 3. График дискретной гармоники частотой 1000 Гц

(Fs = 8192 Гц) и непрерывной.

На рис. 3 видим, что гармоника частотой 1000 Гц, построенная по отсчётам совпадает по форме с непрерывной гармоникой той же частоты, значит, частота отсчётов 8192 Гц достаточна для дискретизации такой гармоники.

Действительно, согласно теореме отсчётов сигнал точно восстанавливается по своим отсчётам, если они взяты с частотой , т.е. в нашем случае .

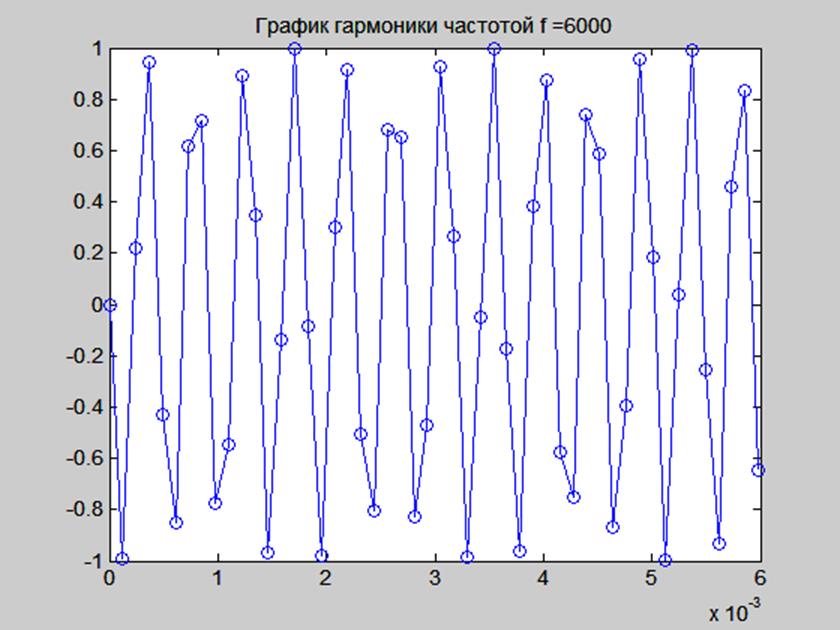
Рис. 4. График гармоники частотой 6000 Гц при частоте отсчётов 8192 Гц.

Увеличим фрагмент рис. 4. и дополним его графиком непрерывной гармоники частотой 6000 Гц для сравнения.

Результат представлен на рис.5.

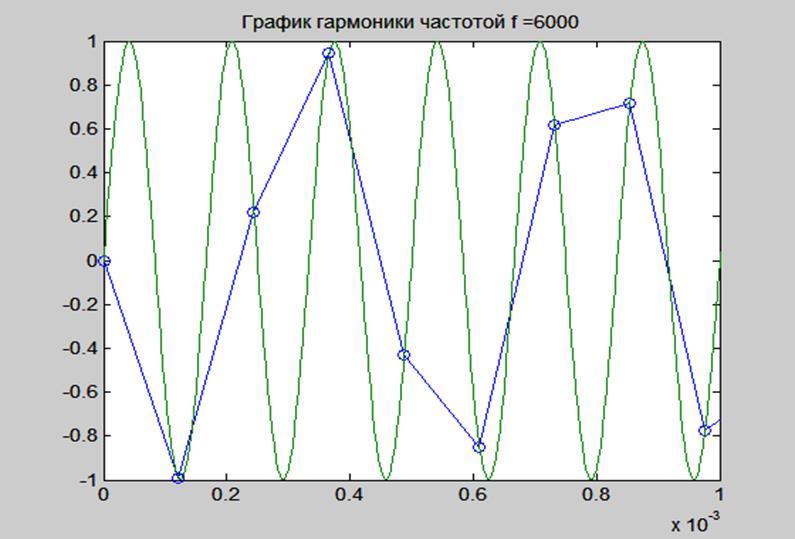
Рис. 5. График дискретной гармоники частотой 6000 Гц

 (Fs = 8192 Гц) и непрерывной.

На рис. 5 видим, что гармонику частотой 6000 Гц не удалось восстановить по отсчётам, взятым с частотой Fs = 8192 Гц.

В данном случае наблюдается наложение гармоник. Гармоника 6000 Гц подменяется на гармонику частотой около 2000 Гц (судя по графику рис. 5).

Это происходит, т.к. не выполняется условие теоремы отсчётов .

При частоте отсчётов Fs = 8192 Гц максимально возможная частота гармоники (частота Найквиста) 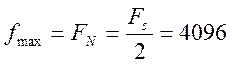 Гц и происходит свёртывание всех гармоник с более высокими частотами относительно частоты .

Таким образом, гармоника частотой 6000 Гц подменяется на гармонику частотой 2000 Гц, что подтвердилось экспериментально.

Прослушав звучание всех сгенерированных сигналов, заметили, что:

- сигналы частотой 2000 и 6000 Гц практически неразличимы на слух;

- сигналы частотой 5000 и 6000 Гц звучат ниже, чем 4000 Гц.

Полученные при прослушивании результаты ещё раз подтверждают наличие явления наложение гармоник при несоблюдении условий теоремы отсчётов.

4.  Построение графиков амплитудных спектров гармонических сигналов различной частоты при частоте отсчётов 8192 Гц.

С помощью следующего script-файла построим графики амплитудных спектров гармонических сигналов частотой 1000 и 6000 Гц при частоте отсчётов 8192 Гц.

f= input('Введите частоту сигнала в Гц   f = ');

fs=8192;

dur=1;

[x,t]=harmonic(2*pi*f,2*pi*fs,dur); %сигнал

Fmax=fs;

df=1/dur;

f=-Fmax/2:df:Fmax/2; % частотная шкала