6.
Генерирование гауссовского случайного сигнала с нулевым средним
значением и дисперсией равной 2, длительностью 1000 отсчетов. Частотная
характеристика фильтра для ![]() . Гауссовский
сигнал рассматривается как входной сигнал фильтра. Графики АЧХ фильтра,
спектральной плотности мощности входного и выходного сигналов.
. Гауссовский
сигнал рассматривается как входной сигнал фильтра. Графики АЧХ фильтра,
спектральной плотности мощности входного и выходного сигналов.
![]() -
оценивает спектральную плотность мощности дискретного по времени сигнала
-
оценивает спектральную плотность мощности дискретного по времени сигнала ![]() и возвращает её в вектор
и возвращает её в вектор ![]() , а в вектор
, а в вектор ![]() возвращает
значения частот, для которых происходит оценка спектральной мощности.
возвращает
значения частот, для которых происходит оценка спектральной мощности.
>> N = 1000;
>> y = random('norm',0,2,1,N);
>> stem(y), grid
>> title('Гауссовский случайный сигнал'), xlabel('n, отсчёт')
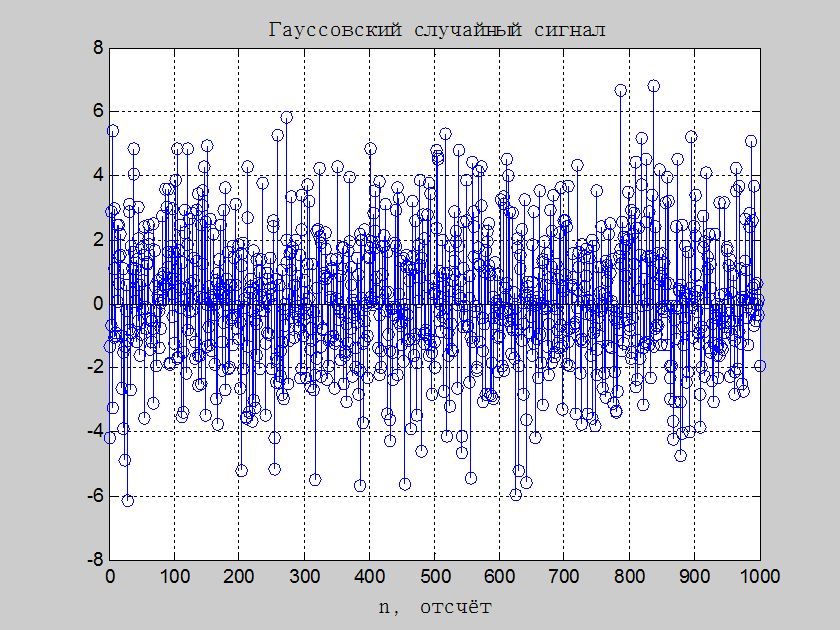
Рис.8. Гауссовский случайный сигнал с нулевым средним значением и дисперсией равной 2
Уравнение фильтра:![]() .
.
Z-преобразование
от левой и правой частей уравнения:![]() .
.
Передаточная функция фильтра: 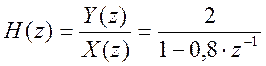 .
.
Частотная характеристика фильтра:
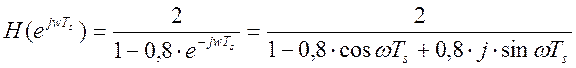 , где
, где ![]() -
интервал отсчётов.
-
интервал отсчётов.
Matlab script (labrab115.m)
%построение частотной характеристики фильтра
Ts = 0.001; %интервал отсчётов
T = 1; %длительность сигнала
df = 1/T;
Fmax = 1/Ts;
f = 0:df:Fmax/2; %частотная шкала
d1 = length(f);
%частотная характеристика фильтра
H = 2./(1-0.8*exp(-j*2*pi*f*Ts));
subplot(3,1,1)
plot(f,abs(H)), title('АЧХ фильтра')
%вычисление и построение спектра мощности входного шума
[Sxx, f1] = psd(y,d1, Fmax); %вычисление спектра мощности входа
subplot(3,1,2)
stem(f1,Sxx), axis([0,500,0,30])
title('Спектр мощности входа')
%вычисление и построение спектра мощности выхода
Y = zeros(1, length(y));
%формирование выходного сигнала фильтра
num = [2];
den = [1, -0.8];
Y = filter(num,den,y);
[Syy, f2] = psd(Y,d1,Fmax); %спектр мощности выхода
subplot(3,1,3)
stem(f2,Syy), axis([0,500,0, 1000])
title('Спектр мощности выхода')
xlabel('f, Гц')
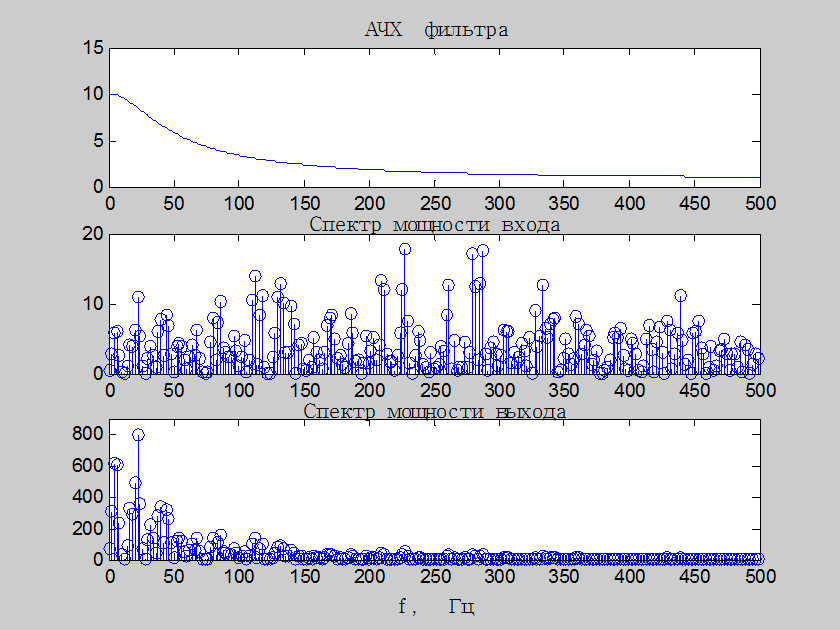
Рис.9. Графики АЧХ,
спектральной плотности мощности входного и выходного сигналов фильтра с
уравнением ![]()
Комментарий: По
аналогии с детерминированными сигналами, для упрощения анализа случайных
сигналов используется частотное преобразование. Эта процедура основывается на
использовании спектральной плотности мощности сигнала: 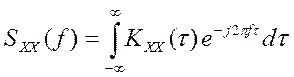 .
СПМ показывает распределение мощности сигнала по частотному диапазону и имеет
размерность Вт/Гц. На рис.9 показаны графики АЧХ фильтра, а также СПМ
входного и выходного сигнала. Система является фильтром нижних частот с
частотой полосы пропускания порядка 36 Гц. При сравнении, не трудно заметить,
что при прохождении сигнала через такой фильтр, средняя мощность низкочастотных
составляющих сигнала усиливается, а высокочастотных – наоборот, ослабляется.
Так значения средней мощности при f>150 Гц
практически не отличаются от нуля, поскольку приходятся на полосу задерживания
фильтра. Мощность выходного сигнала в полосе пропускания фильтра
пропорциональна квадрату коэффициента передачи фильтра
.
СПМ показывает распределение мощности сигнала по частотному диапазону и имеет
размерность Вт/Гц. На рис.9 показаны графики АЧХ фильтра, а также СПМ
входного и выходного сигнала. Система является фильтром нижних частот с
частотой полосы пропускания порядка 36 Гц. При сравнении, не трудно заметить,
что при прохождении сигнала через такой фильтр, средняя мощность низкочастотных
составляющих сигнала усиливается, а высокочастотных – наоборот, ослабляется.
Так значения средней мощности при f>150 Гц
практически не отличаются от нуля, поскольку приходятся на полосу задерживания
фильтра. Мощность выходного сигнала в полосе пропускания фильтра
пропорциональна квадрату коэффициента передачи фильтра 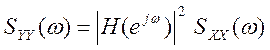 .
В данном случае
.
В данном случае 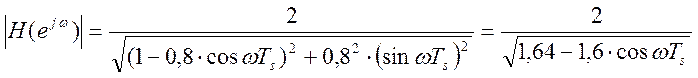 , т.о. на нулевой частоте
должно происходить усиление СПМ входного сигнала в 100 раз.
, т.о. на нулевой частоте
должно происходить усиление СПМ входного сигнала в 100 раз.
Вывод по работе: Детерминированные сигналы по своей сути не могут дать никаких новых сведений, поэтому такие сигналы могут представлять интерес только как тестовые последовательности изучения поведения систем. Сигналы, получаемые в результате измерений, носят, как правило, случайный характер. Описание таких сигналов основывается на использовании математических моделей с использованием теории случайных процессов. В данной работе были изучены основные характеристики случайных стационарных сигналов:
Вследствие проведённых экспериментов было выявлено, что при конкретной реализации случайного сигнала всё время получается новая функция, описывающая этот закон распределения, а, следовательно, и изменяются значения среднего и дисперсии от заданных теоретических (см п.1). Но если увеличивать количество значений выборки, то и характеристики случайного сигнала будут всё более приближаться к теоретическим значениям.
Важной и наиболее полной является функция плотности вероятности случайного сигнала, которая позволяет установить – какова вероятность появления значения случайного сигнала. Если обратиться к п.2 данной работы, то можно наблюдать, что более вероятно встретить нулевое значение и значения максимально к нему приближенные. Вероятность в этом случае составляет – 43%.
Важнейшей функцией анализа случайного сигнала является автокорреляционная функция, которая определяет, насколько сильна связь между отсчетами сигнала, разделенными друг от друга интервалом m. Любой реальный процесс имеет конечную память, поэтому для таких сигналов с увеличением интервала m между отсчетами степень связи должна ослабевать. Вышесказанное можно пронаблюдать с помощью рис.4 и рис.5, на которых показаны графики рассеяния значений Yi+m относительно значений Yi. Очевидно, что для коррелированных сигналов график должен иметь линейную зависимость, т.о. можно судить о степени коррелированности сигналов – чем график больше напоминает линейную зависимость, тем сильнее коррелированны сигналы и наоборот.
При исследовании входного и выходного сигналов системы полезно использовать взаимную корреляционную функцию сигнала, которая характеризует связь между двумя сигналами. На рис.7 продемонстрирована эта зависимость. Сильнее всего зависят значения выходного сигнала от значений входного сигнала в моменты времени 0, 1 и 2. В идеале график ВКФ должен представлять из себя три единичных импульса, определённые в эти моменты времени, но т.к. здесь входной сигнал является выборкой конечной длины, то соответственно появляется погрешность.
Для случайных
сигналов также возможен частотный анализ. Переход в частотную область
осуществляется за счет преобразования 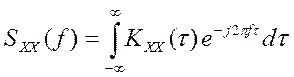 ,
Sxx(f)
– спектральная плотность мощности случайного сигнала, аналогична преобразованию
Фурье для детерминированного сигнала.
,
Sxx(f)
– спектральная плотность мощности случайного сигнала, аналогична преобразованию
Фурье для детерминированного сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.