subplot(313), plot(f,angle(y1p)), title('Фазовый спектр')
xlabel('Частота, Гц')
Результатом выполнения данного Script-файла – построение графиков амплитудного и фазового спектров одностороннего экспоненциального сигнала с помощью функции dftsum().
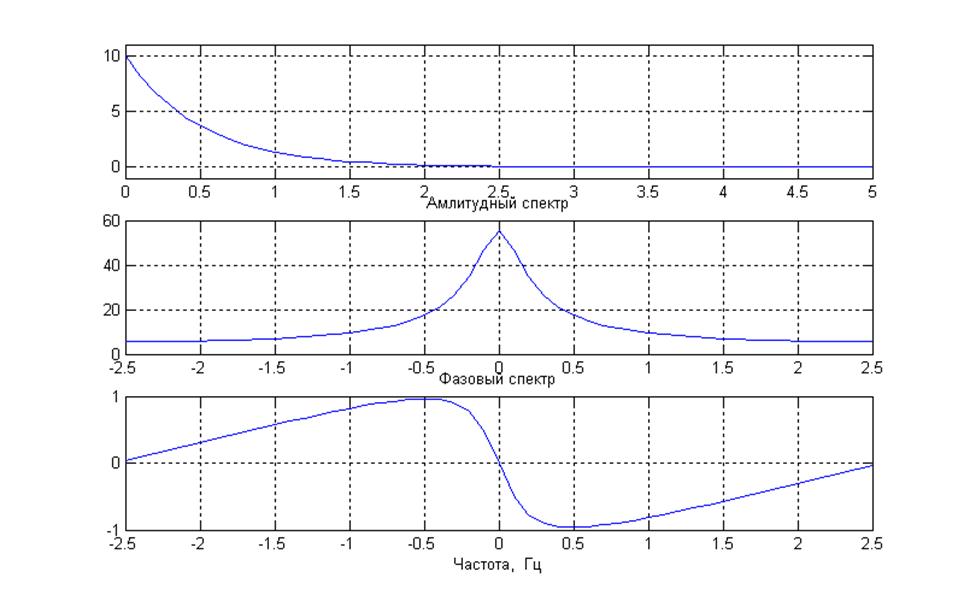
Рис.4 Графики одностороннего экспоненциального сигнала,
его амплитудного и фазового спектров построенных через dftsum().
7. Проведение вычисления и построения графиков спектров сигнала с помощью функции fft().
Листинг Script-файла p7.m
%Script-файл для сравнения амплитудных спектров одного и того же сигнала
%построенных с помощью аналитических вычислений и с помощью функции MatLab
%fft()
T=5;
N=128; % число точек
Ts=T/(N-1); % интервал отсчетов
t=0:Ts:T; % временной интервал
K=10;
a=2;
x=K*exp(-a*t); % генерирование импульса
figure(1);
subplot(311), plot(t, x) % график сигнала
title(' График сигнала')
Fmax=1/Ts; % максимальная частота
df=1/T; % частотное разрешение
f=-Fmax/2:df:Fmax/2; % частотная шкала
X=fft(x,N); % БПФ сигнала
Xp=fftshift(X); % частотный сдвиг
A=abs(Xp);
subplot(312), plot(f,A*Ts)
title('fft- Амплитудный спектр сигнала')
S=K./(a+j*f); % выражение %комплексного спектра
subplot(313), plot(f, abs(S))
xlabel(' Частота, Гц')
title(' Амплитудный спектр сигнала ')
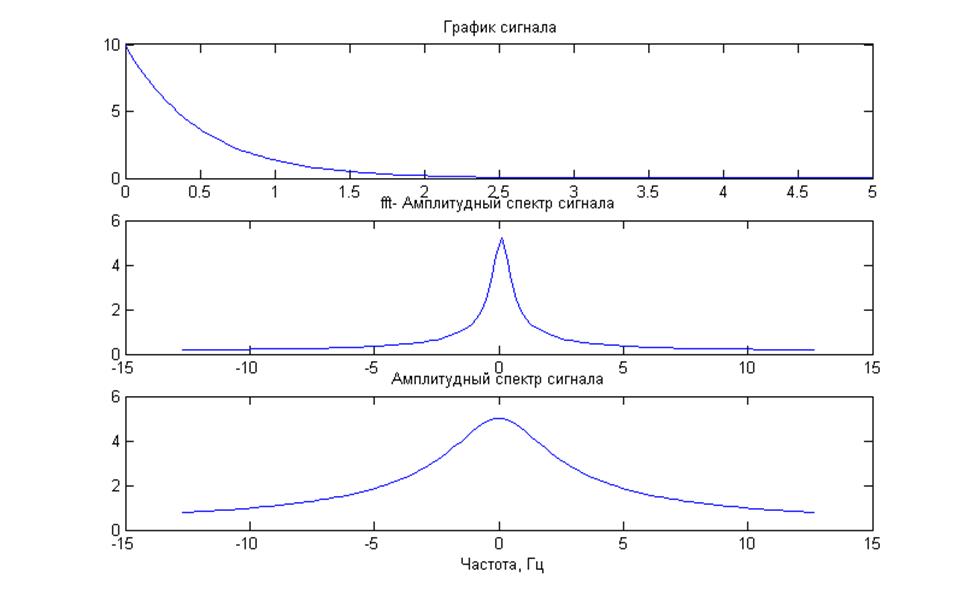
Рис.5 Графики амплитудного спектра сигнала 1 (2 - с помощью fft(),3 - аналитический)
8. Изучение свойств преобразования Фурье:
(с помощью процедуры из Приложения 5)
% Процедура иллюстрации свойств преобразования Фурье
N = 128; % Длина сигналов
k = 0:N-1;
gamma = -0.5;
g = exp(gamma*k);
% g - экспоненциальная функция
h = sin(2*pi*k/(N/2));
figure(1),plot(k,g,k,h)
% h - синусоидальная последовательность с периодом = N/2
% вычисление преобразований Фурье сигналов
[G,w] = freqz(g,1,512);
[H,w] = freqz(h,1,512);
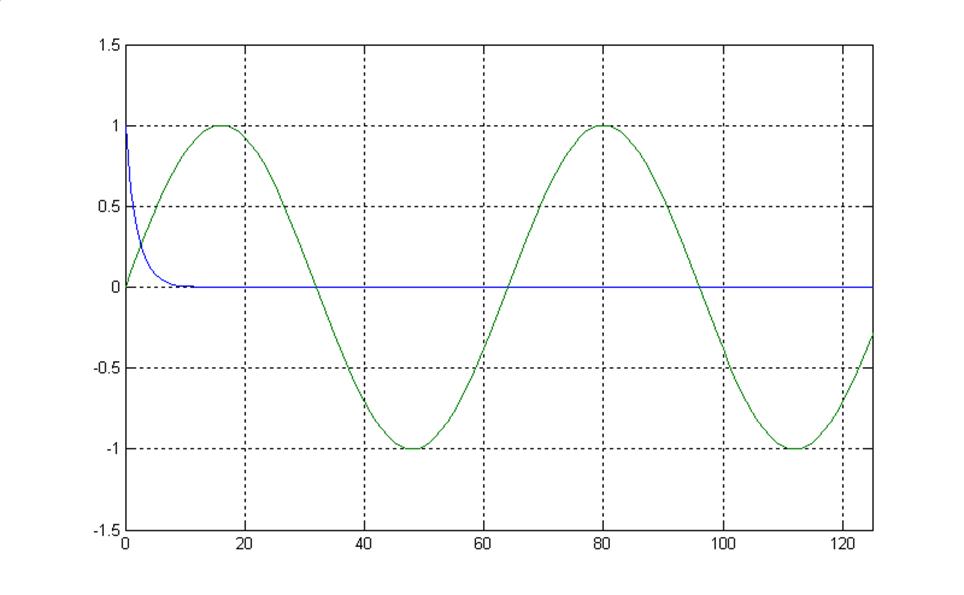
Рис.6 Графики исходных сигналов
% Свойство линейности
alpha = 0.5;
beta = 0.25;
y = alpha*g+beta*h;
[Y,w] = freqz(y,1,512);
% Графики Y и alpha*G+beta*H для проверки их равенства
figure(2), subplot(211),plot(abs(Y))
subplot(212), plot(abs(alpha*G+beta*H))
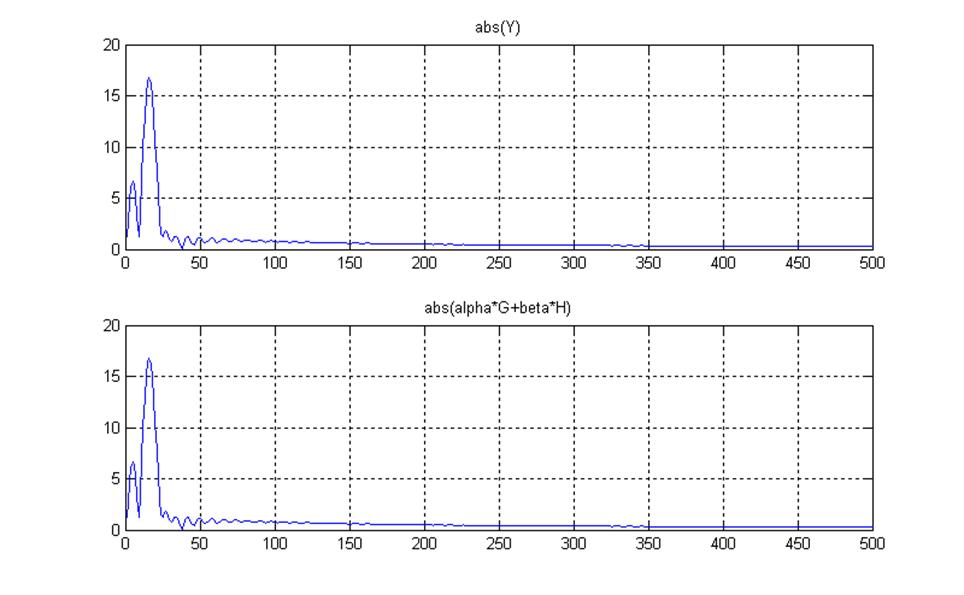
Рис.7 Иллюстрация свойства линейности
Комментарии:
Y – это спектр суммы исходных сигналов, а alpha*G+beta*H – сумма спектров исходных сигналов. Идентичность графиков показывает справедливость свойства линейности преобразований Фурье.
% Свойство временного сдвига
n0 = 12;
% y2 - последовательность y, сдвинутая на 12 отсчетов
y2 = [zeros([1,n0]) g];
[Y2,w] = freqz(y2,1,512);
G0 = exp(-j*w*n0).*G;
% Графики амплитудных спектров
figure(3), subplot(211), plot(abs(G0))
subplot(212), plot(abs(Y2));
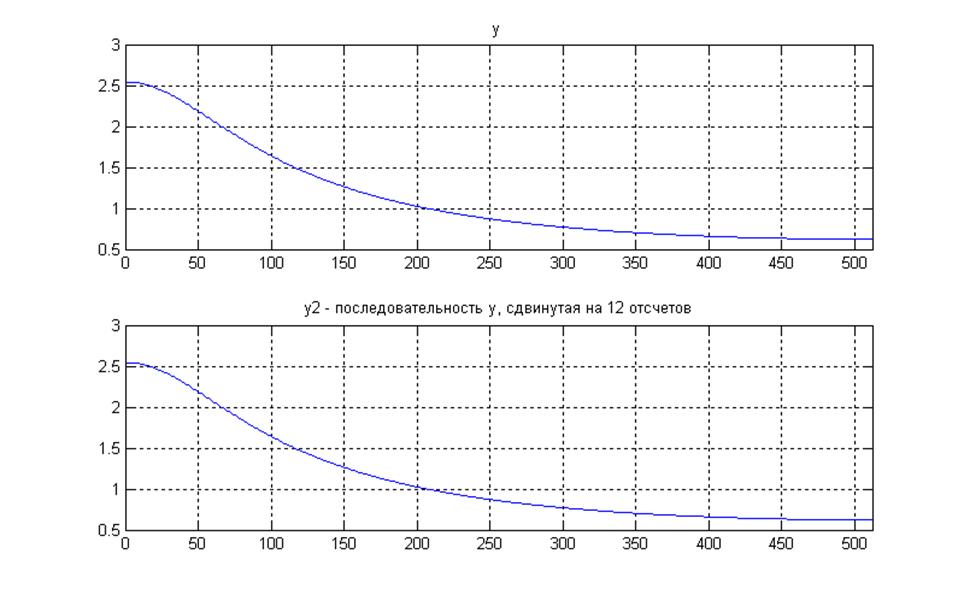
Рис.8 Иллюстрация свойства временного сдвига
Комментарии:
При сдвиге во времени меняется только фазовый спектр, , и не меняется амплитудный.
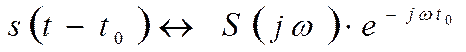
При сдвиге функции на t0, модуль S(ω) не изменяется, а сдвигается во времени на t0.
% Свойство изменения масштаба
a=0.1; % Коэффициент изменения масштаба
g1= exp(gamma*k*a);
figure(4),plot(k,g,k,g1) % Графики во временной области
[G,w] = freqz(g,1,512);
G1 = freqz(g1,1,512);
% Графики спектров
figure(5), subplot(211), plot(w',abs(G))
subplot(212), plot(w,abs(G1))
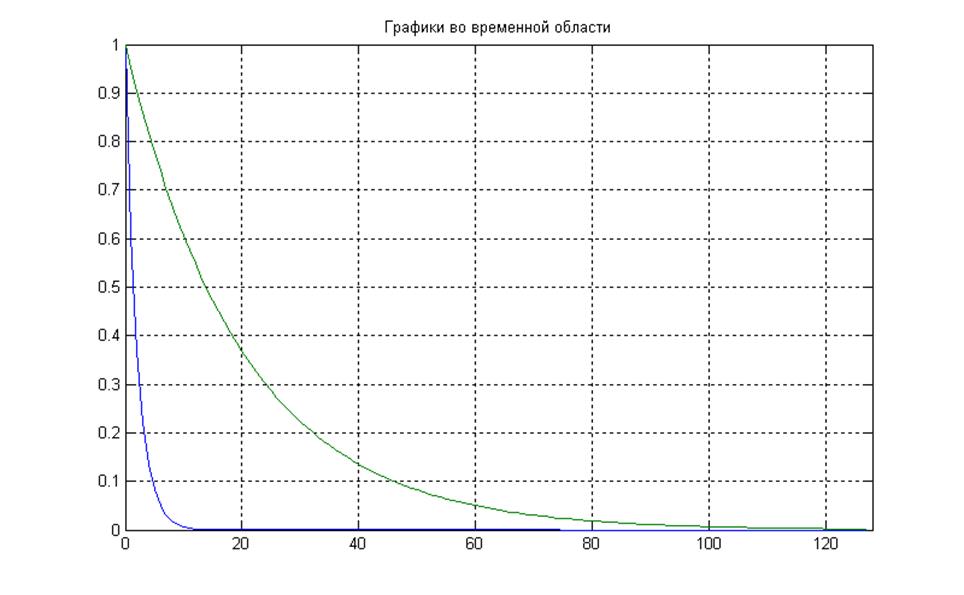
Рис.9 Графики сигналов во временной области
(коэффициент масштабирования а = 0.1)
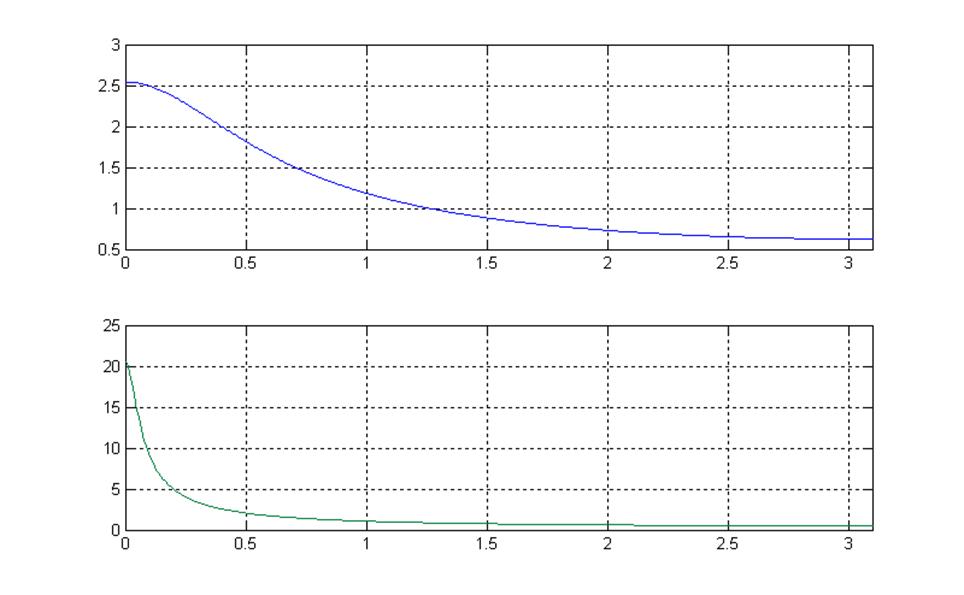
Рис.10 Графики спектров (а = 0.1)
Комментарии:
При данном изменении масштаба:
% Свойство свертки
y5 = conv(g,h);
[Y5,w] = freqz(y5,1,512);
figure(6), subplot(211), plot(abs(Y5))
subplot(212), plot(abs(G.*H))
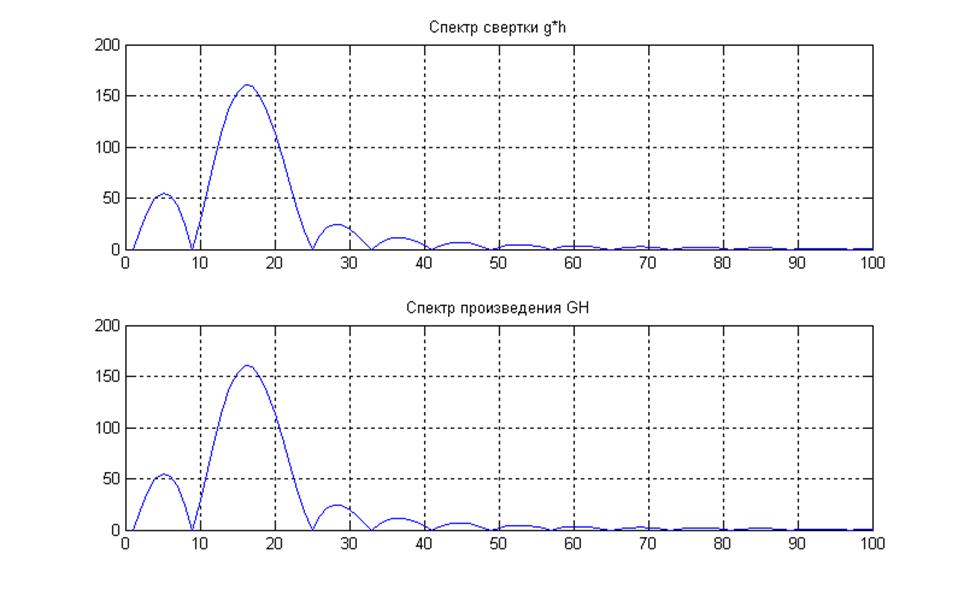
Рис.11 Иллюстрация свойства свертки.
Комментарии:
Спектр свертки равен спектру произведения преобразований Фурье сигналов.
% Теорема Парсеваля
H0 = exp(-j*w*n0).*H;
val1 = sum(g.*conj(h));
val2 = sum(G0.*conj(H0))/512;
% Сравнение val1 с val2
disp('Разность val1-val2 = ')
disp(val1-val2)
Результат работы:
>> Разность val1-val2 =
0.0000 - 1.3618i
Комментарии:
Теорема Парсеваля заключается в том, что полная энергия сигнала равна сумме энергий всех его частотных составляющих. Однако энергетический спектр не содержит информацию о фазах гармоник сигнала, и, значит, эта часть сведений о сигнале из его энергетического спектра не может быть получена.
Теорема Парсеваля: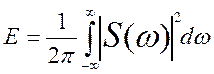
Выводы:
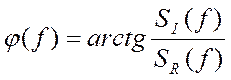 . Она отражает зависимость
распределения начальных фаз гармоник от частоты сигнала.
. Она отражает зависимость
распределения начальных фаз гармоник от частоты сигнала. 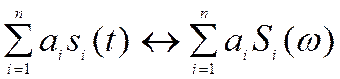
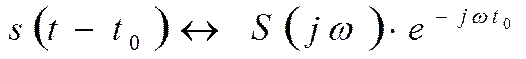
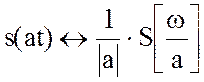
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.