Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра ССОД
Дисциплина «Теория и обработка сигналов»
ЛАБОРАТОРНАЯ РАБОТА № 5
НЕПРЕРЫВНАЯ И ДИСКРЕТНАЯ СВЕРТКИ
ВАРИАНТ №9
Выполнила: Проверил:
Баранова К.В. доц. Щетинин Ю.И.
Группа: АО-61
Новосибирск, 2008
Цель работы:изучение понятия и свойств непрерывной и дискретной свертки, приобретение практических навыков вычисления свертки в среде Matlab.
1. Изучение непрерывной свертки на примере свертки прямоугольного импульса и экспоненциального сигнала.
Код MatLab:
% Численное вычисление непрерывной свертки
%
T=0.1; % шаг дискретизации
a=5;
i=0:50;
x1=exp(-a*i*T); % сигнал x1
x2=rectpuls(i-10,20); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i*T,x1), title('x1')
subplot(412), plot(i*T,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Svertka x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Svertka function conv')
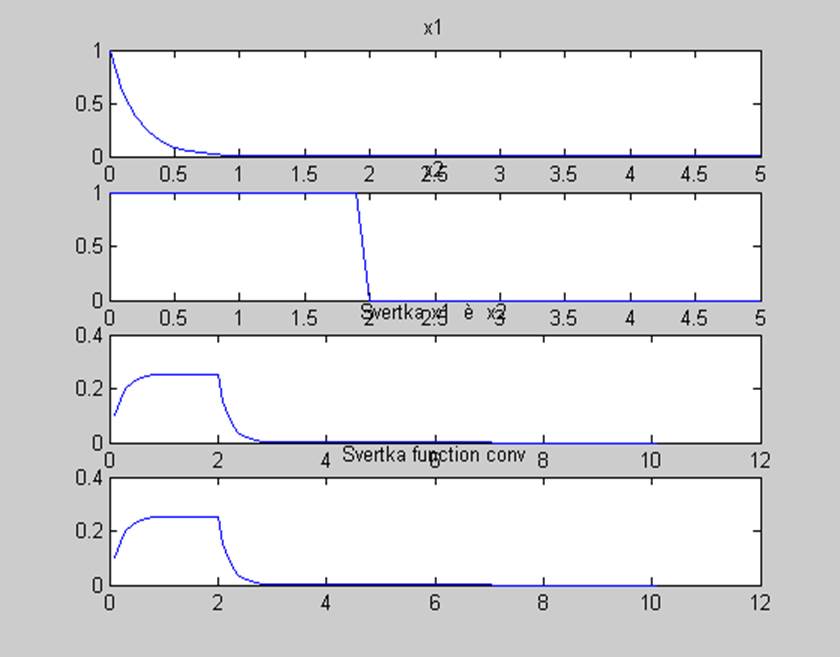
Рис.1. Сверткаа сигналов.
Комментарий:
Свертка двух непрерывных по времени сигналов (непрерывная свертка) определяется выражением
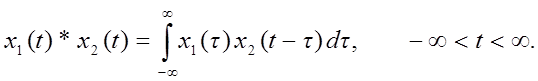
Ее численное вычисление может быть аппроксимировано конечной суммой вида
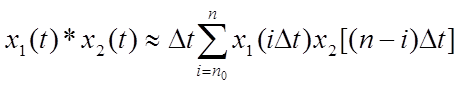 .
.
Из графиков видно, что вычисление линейной свертки с помощью конечных сумм и с помощью функции conv идентичны.
2. Выполнение процедуры вычисление непрерывной свертки для заданных сигналов:
. 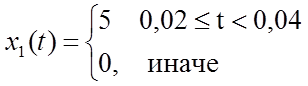 ,
, 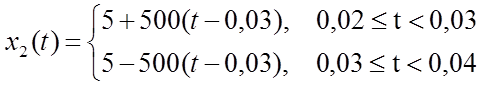
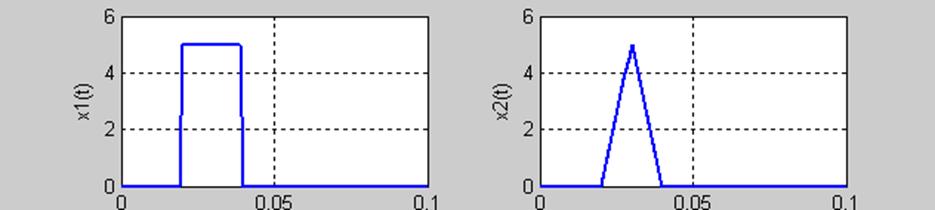
Рис.2. Графики заданных сигналов.
Код MatLab:
% Численное вычисление непрерывной свертки
T=0.1; % шаг дискретизации
a=5;
i=0.02:0.001:0.05;
x1=a*tripuls(i-0.03,0.02); % сигнал x1
x2=a*rectpuls(i-0.03/2,0.05); % сигнал x2
n1=length(x1);
n2=length(x2);
figure(2),subplot(411), plot(i,x1), title('x1')
subplot(412), plot(i,x2), title('x2')
k1=1:n1+n2-1;
% вычисление свертки
for n=1:n1+n2-1,
y(n)=0;
for k=max(1,n+1-n1):min(n,n2),
y(n)=y(n)+sum(x1(n+1-k)*x2(k));
end
y(n)=y(n)*T;
end
% график свертки сигналов
subplot(413), plot(k1*T,y),title('Svertka x1 и x2')
% вычисление свертки с помощью функции conv()
subplot(414), plot(k1*T,T*conv(x1,x2))
title('Svertka function conv')
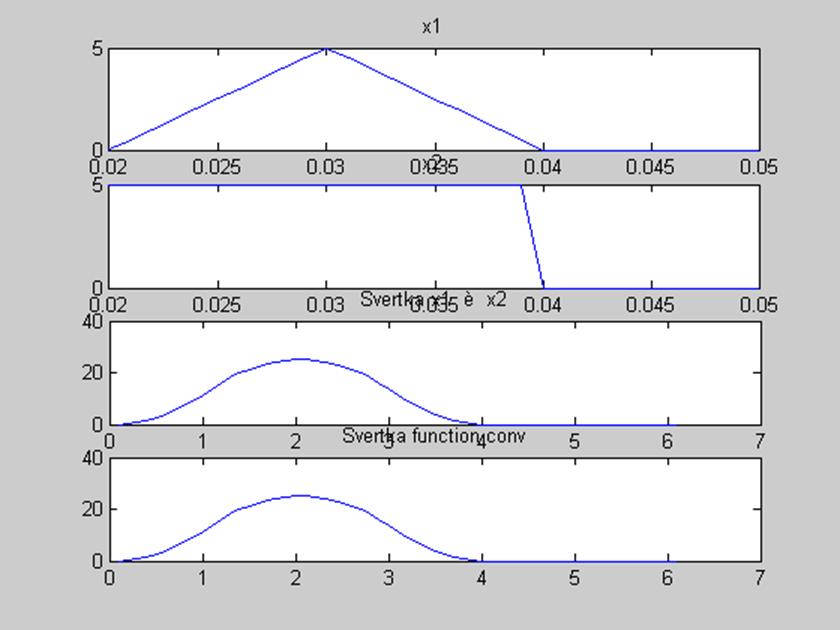
Рис.3.Графики сигналов и их свертка.
Комментарии:
Графики свертки полученные с помощью вычисления конечных сумм и с помощью использования функции conv() пакета MatLab полностью совпадают.
3. Синтаксис функции conv() пакета MatLab, для свертки дискретных во времени сигналов.
CONV Свертка дискретных во времени сигналов.
C = CONV (A, B) производит свертку векторов A и B.
Результат операции - вектор длиной LENGHT(A) +LENGTH (B)-1.
Аналитически свертка дискретных по времени сигналов определяется следующим выражением:
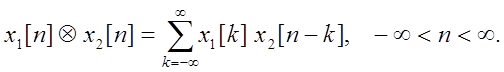
4. Синтаксис функции sqgen(L, T) для генерации прямоугольной последовательности импульсов (прямоугольной волны) длиной L отсчетов и периодом T отсчетов.
Код Matlab:
function x=sqgen(L,T)
t = 0:L-1;
y = square(2*pi*(t/T));
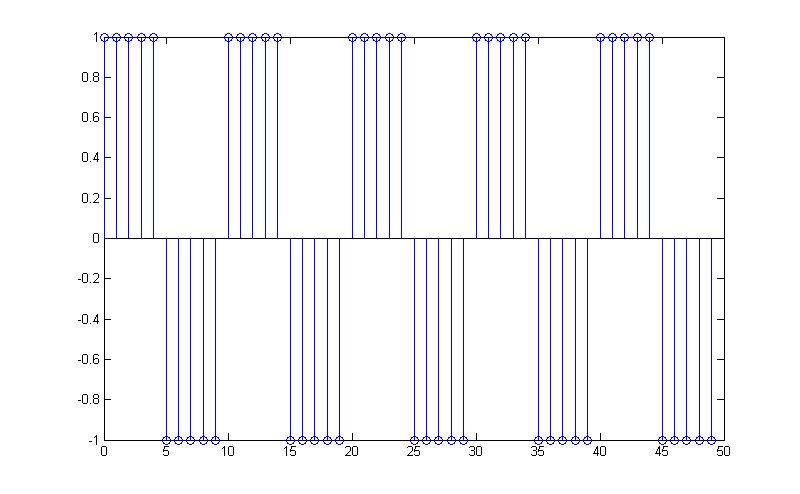
Рис.4. Пример работы функции sqgen(L,T).
5. Вычисление свертки единичного импульса delta1 и sqgen(50, 10).
Код Matlab:
% Построение графиков единичного скачка, прямоугольной волны и их свертки
L=50;
t = 0:L-1;
%для единичного импульса
d1=[1]
%для прямоугольной волны
x=sqgen(50,10)
%построение графиков
N=0:1+50-1
subplot(311), stem( d1),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('График единичного скачка');
subplot(312), stem( t,x),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('График прямоугольной волны');
subplot(313), stem(conv(d1,x)),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Вычисление свертки с помощью conv');
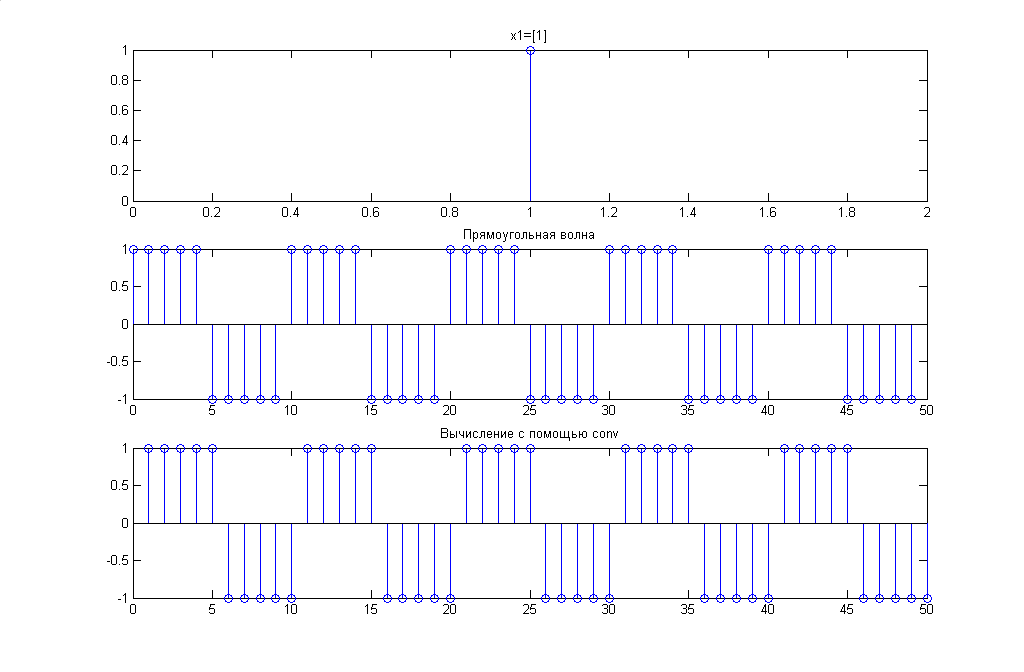
Рис.5. Графики единичного скачка, прямоугольной волны и их свертки
Комментарий:
Аналитически дискретная свертка вычисляется следующим выражением:
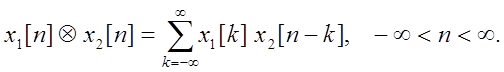
для x 1= {1} и
любого x2 , свертка 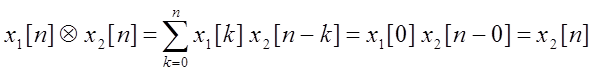
6. Вычисление свертки единичного импульса delta2 и sqgen(50, 10).
Код Matlab:
% Построение графиков единичного скачка, прямоугольной волны и их свертки
L=50;
t = 1:L;
%для единичного импульса
d2=[1 zeros(1,9)];
%для прямоугольной волны
x=sqgen(50,10);
%построение графиков
N=1:60-1;
subplot(311), stem(d2),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('График единичного скачка');
subplot(312), stem(t, x),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('График прямоугольной волны');
subplot(313), stem(N, conv(d2,x)),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Вычисление свертки с помощью conv');
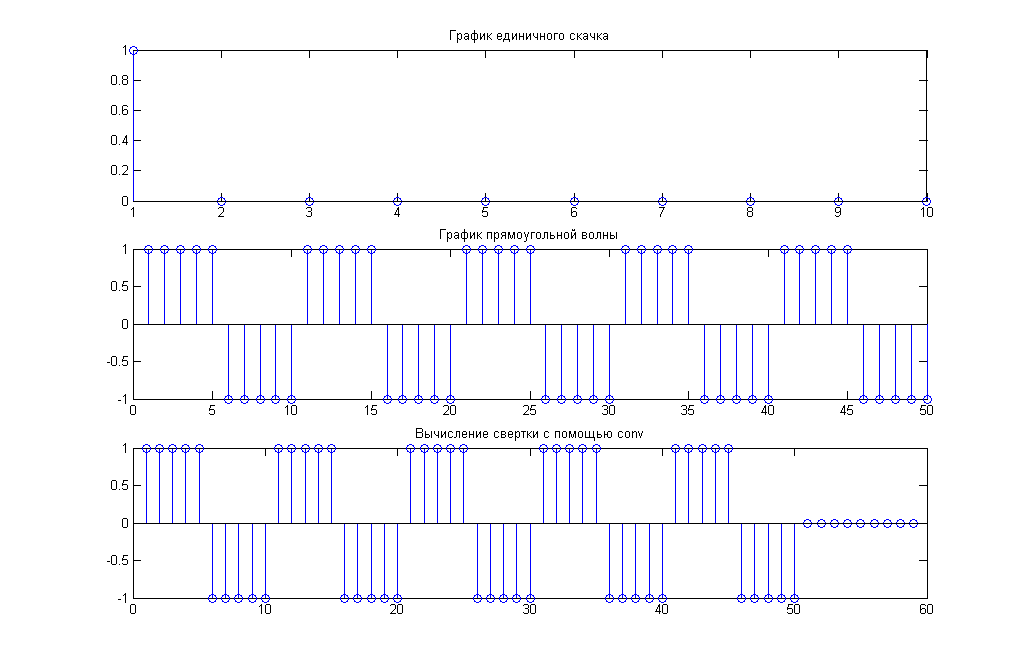
Рис.6. Сигнал D2, прямоугольная волна и их свертка
Комментарии:
7. 1)Создание плоского импульса длительностью 2 отчета, прямоугольной волны, вычисление их свертки.
Код Matlab:
i=0:49;
x1=[ones(1,2)];
x2=sqgen(50,10);
n1=length(x1);
n2=length(x2);
N=1:n1+n2-1;
subplot(311), stem(x1),
title('x1=[ones(1,2)]')
set(gca,'FontName','Verdana Cyr','FontSize',9)
subplot(312), stem(i,x2),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Прямоугольная волна')
subplot(313), stem(N, conv(x1,x2)),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Вычисление с помощью conv')
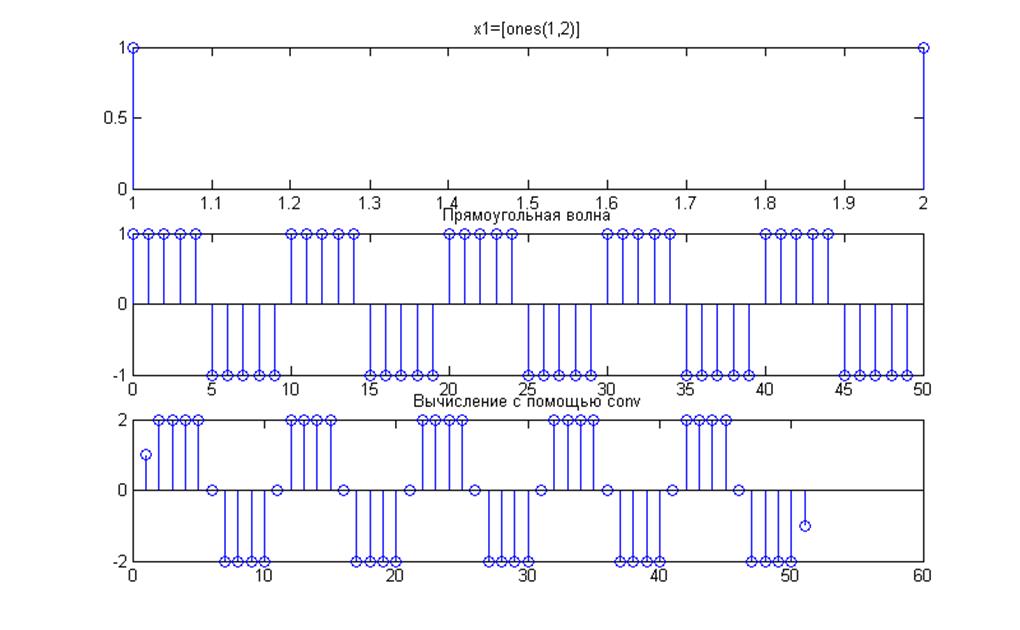
Рис.7. Графики сигналов x1=[ones(1,2)] и x2=sqgen(50,10) и их свертка
2)Увеличение длительности плоского сигнала до 8 отсчетов.
Код Matlab:
i=0:49;
x1=[ones(1,8)];
x2=sqgen(50,10);
n1=length(x1);
n2=length(x2);
N=1:n1+n2-1;
subplot(311), stem(x1),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('x1=[ones(1,8)]')
subplot(312), stem(i,x2),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Прямоугольная волна')
subplot(313), stem(N,conv(x1,x2)),
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Вычисление с помощью conv')
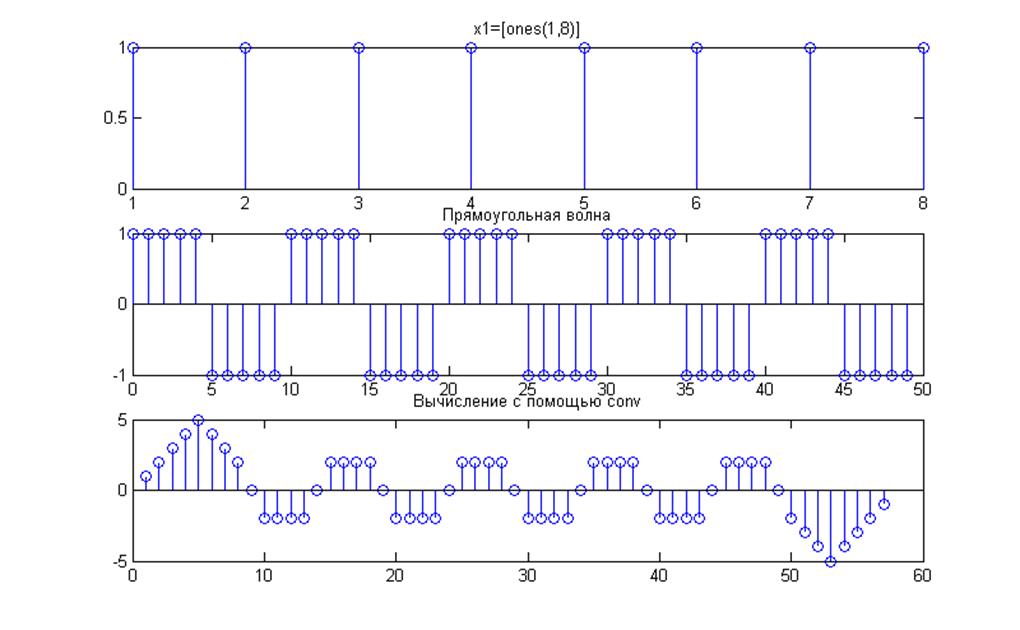
Рис.8. Графики сигналов x1=[ones(1,8)] и x2=sqgen(50,10) и их свертка
Комментарии:
Из рис.8 и рис.7 видно, что при увеличении длительности первого сигнала, свертка изменяет свой вид таким образом, что на концах свертки происходит изменение прямоугольных импульсов к треугольным.
8. Вычисление свертки двух сигналов Х1 и Х2 и восстановление сигнала Х1 из свертки.
Код Matlab:
n=20;
i=0:n-1;
t=-5:5;
x1=sinc(t/pi);
x2=u(i)-u(i-5);
subplot(411), stem(t,x1)
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Сигнал х1')
subplot(412), stem(x2),title('Сигнал х2')
x=conv(x1,x2);
subplot(413), stem(x)
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Вычисление свёртки с помощью conv')
subplot(414), stem(t,deconv(x,x2))
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Восстановление х1')
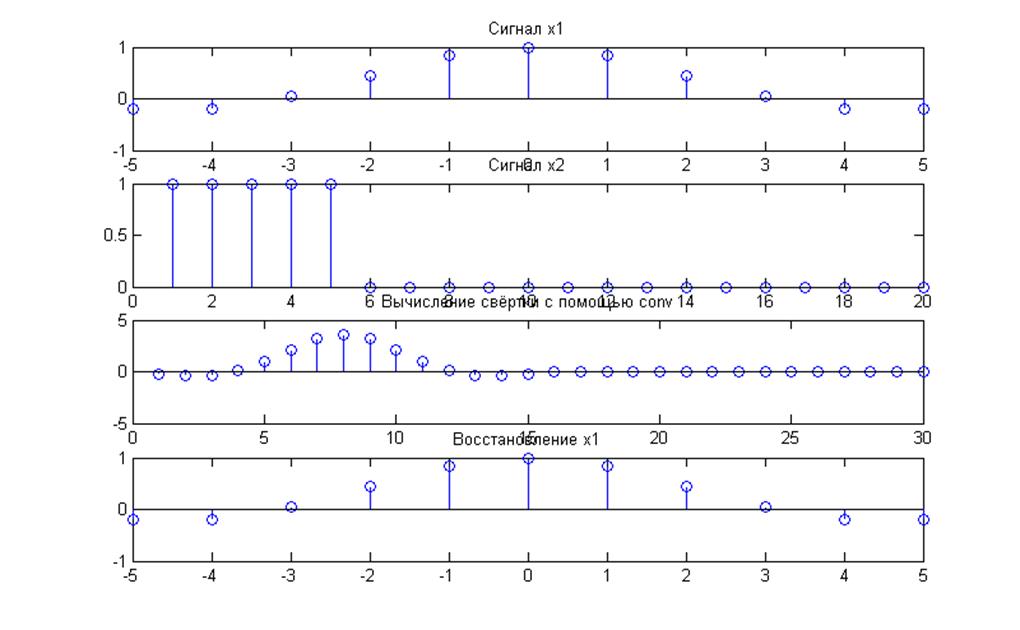
Рис.9. Восстановление сигнала х1 из свертки с использованием функции deconv().
Комментарии:
Из графика видно, что сигнал х1 полностью восстановлен из свертки с помощью функции deconv().
9. Дискретная и круговая свёртки дискретного экспоненциально убывающего и прямоугольного сигналов.
Код Matlab:
n=0:0.1:9.9;
k=0:0.1:3.9;
t=0:138;
t2=0:255;
y1=exp(-n);
subplot(4,1,1); stem(n,y1);
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Экспоненциально убывающий дискретный сигнал')
y2=rectpuls(k-20,40);
subplot(4,1,2); stem(k,y2);
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Прямоугольный сигнал')
% дискретная свертка сигналов
t1=cputime;
for i=1:1000;
sv=conv(y1,y2);
end;
t_conv=(cputime - t1)/1000
subplot(4,1,3); stem(t,abs(sv));
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Дискретная свертка сигналов(conv)');
% круговая свертка сигналов
y1d=[y1 zeros(1,156)];
y2d=[y2 zeros(1,216)];
t1=cputime;
for i=1:1000;
z1=fft(y1d);z2=fft(y2d);
z3=z1.*z2; sv2=ifft(z3);
end
t_fft=(cputime - t1)/1000
subplot(4,1,4); stem(t2, abs(sv2));
set(gca,'FontName','Verdana Cyr','FontSize',9)
title('Дискретная свертка сигналов(fft)');
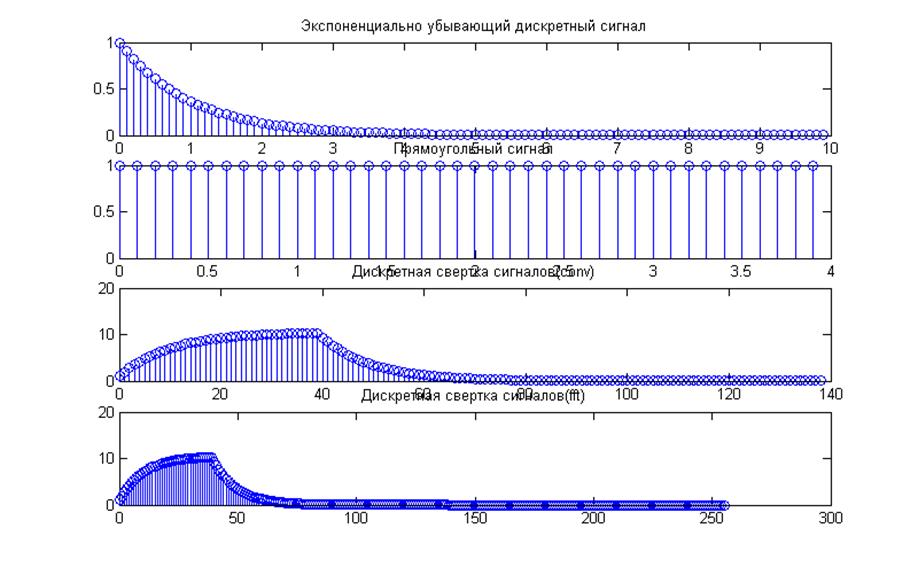
Рис.10. Дискретная и круговая свёртки экспоненциально убывающего и прямоугольного сигналов.
t_conv =
3.010000000000162e-004
t_fft =
2.199999999999989e-004
Комментарии:
Из
результатов выполнения script-файла видно, что свертки полностью совпадают по
форме, а вот время выполнения различное: при использовании conv() время
составило ![]() , а при использовании круговой
свертки, благодаря использованию алгоритмов БПФ, время составило:
, а при использовании круговой
свертки, благодаря использованию алгоритмов БПФ, время составило: ![]() т.е. в 1,36 раза быстрее.
т.е. в 1,36 раза быстрее.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.