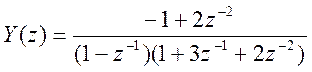 (**)
(**)
Обратное Z – преобразование выражения (**) дает искомое решение во временной области.
Для нахождения обратного Z – преобразования найдём полюса выражения (**) и разложим его на простые дроби.
Полюса:![]()
Разложение Y(z) на простые дроби:
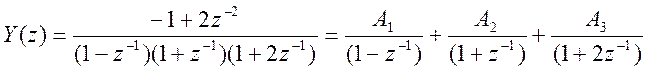 (***)
(***)
Найдём значения коэффициентов числителей дробей
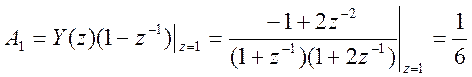
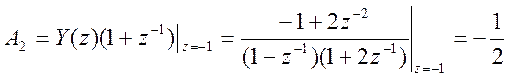
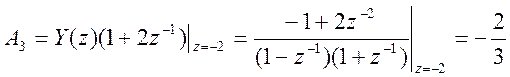 .
.
Подставив в (***)
найденные значения коэффициентов, получим итоговое разложение Y(z) на простые дроби: 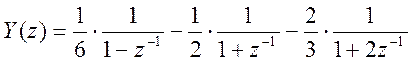
Воспользовавшись
соотношением ![]()
![]()
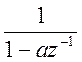 , найдём обратное Z – преобразование Y(z), являющееся решением
исходного уравнения:
, найдём обратное Z – преобразование Y(z), являющееся решением
исходного уравнения:
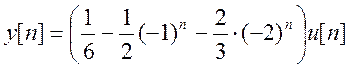 (#)
(#)
Проверим
полученное решение, подставляя значения ![]() в
выражения (#) и (##), полученное из исходного уравнения:
в
выражения (#) и (##), полученное из исходного уравнения:
![]() (##)
(##)
![]()
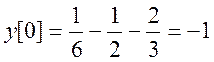
![]()
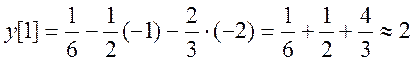
Полученные значения совпадают с определённой погрешностью, поэтому на основании проверки можно сделать вывод о том, что решение возможно верно (кривая решения может пересекаться в одной точке с бесконечным количеством любых кривых, если точек пересечения две, то количество возможных для пересечения линий уменьшается, если три – то ещё больше уменьшается и т.д.).
6. Определение Z – преобразования и ДВПФ сигнала аналитически.
Прямое ДВПФ
имеет вид 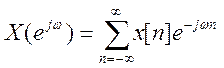 (###)
(###)
Здесь ![]() - непрерывная функция от ω, а x[n] – дискретный по времени сигнал.
- непрерывная функция от ω, а x[n] – дискретный по времени сигнал.
Выражение
обратного ДВПФ: 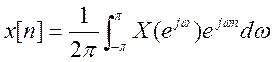 .
.
ДВПФ – это Z – преобразование на единичной окружности, т.е. при ![]() .
.
Вычислим Z – преобразование сигнала 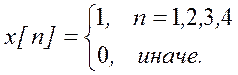 аналитически,
используя формулу суммы конечной геометрической прогрессии. Получим:
аналитически,
используя формулу суммы конечной геометрической прогрессии. Получим:
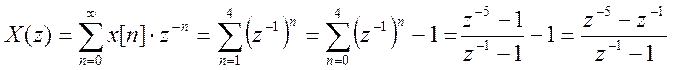
Учитывая, что
ДВПФ – это Z – преобразование при ![]() , получим выражение ДВПФ сигнала вида
, получим выражение ДВПФ сигнала вида
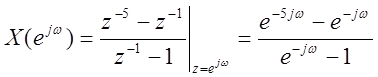
Такой же вид ДВПФ можно получить, воспользовавшись выражением (###).
7. Определение ДВПФ сигналов с помощью Matlab.
Пользовательская функция DTFT( ) Matlabвычисляет дискретно-временное преобразование Фурье с помощью ДПФ.
function [X,w] = DTFT(x,M)
% Функция вычисляет значения DTFT от вектора x.
% Обращение [X,w] = DTFT(x,0)
% здесь X - вектор значений DTFT,
% w - вектор угловых частот.
% Если желательно вычислить DTFT с M значениями частоты,
% используется обращение [X,w] = DTFT(x,M)
% Этот вариант используется, когда размер вектора x
% меньше размера вектора частот w,
% при этом x дополняется нулевыми значениями
N = max(M,length(x));
% Приведение FFT к размеру 2^m
N = 2^(ceil(log(N)/log(2)))
% Вычисление fft
X = fft(x,N);
% Вектор частот
w = 2*pi*( (0:(N-1))/N );
w = w - 2*pi*(w>=pi)
% Сдвиг FFT к интервалу от -pi до +pi
X = fftshift(X);
w = fftshift(w);
С помощью функции DTFT( ) определим ДВПФ следующих сигналов и построим графики их амплитудного и фазового спектров.
а) x[n] = e -0,5n
Для определения ДВПФ сигнала и построения графиков его амплитудного и фазового спектров воспользуемся следующим script-файлом.
n=0:1:15;
x=exp(-0.5*n);
[X,w]=DTFT(x,64)
subplot(3,1,1);
stem(n,x);
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Cигнал');
subplot(3,1,2);
plot(w,abs(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Амплитудный спектр');
subplot(3,1,3);
plot(w,angle(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Фазовый спектр');
Результат представлен на рис. 1.
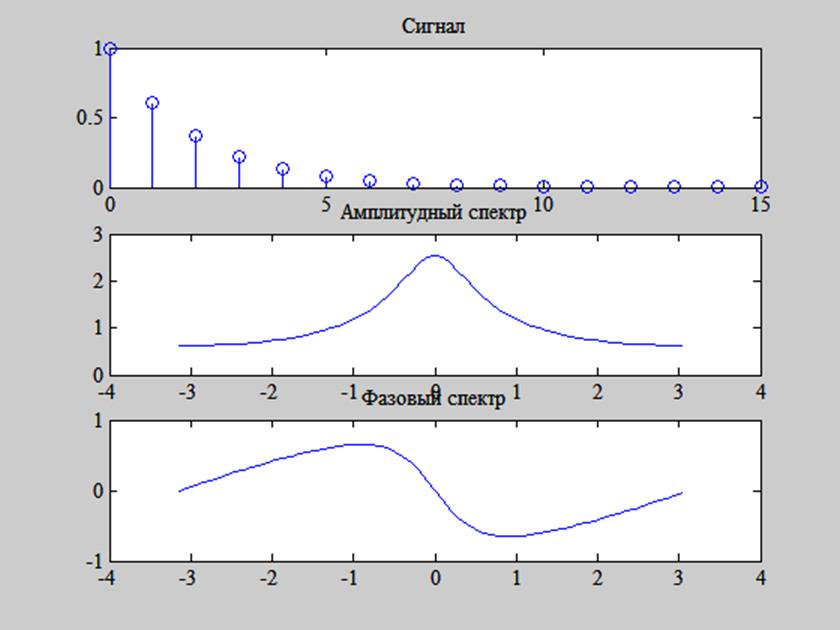
Рис. 1. График сигнала x[n] = e -0,5n и его амплитудного и фазового спектров.
Видим, что спектры дискретного сигнала x[n] = e -0,5n непрерывны. График амплитудного спектра сигнала обладает чётной симметрией, а фазового спектра – нечётной.
б) 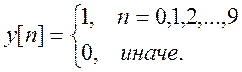
Для определения ДВПФ сигнала и построения графиков его амплитудного и фазового спектров воспользуемся следующим script-файлом.
n=0:1:9;
x=[ones(1,10)];
[X,w]=DTFT(x,64)
subplot(3,1,1);
stem(n,x);
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Cигнал');
subplot(3,1,2);
plot(w,abs(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Амплитудный спектр');
subplot(3,1,3);
plot(w,angle(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Фазовый спектр');
Результат представлен на рис. 2.
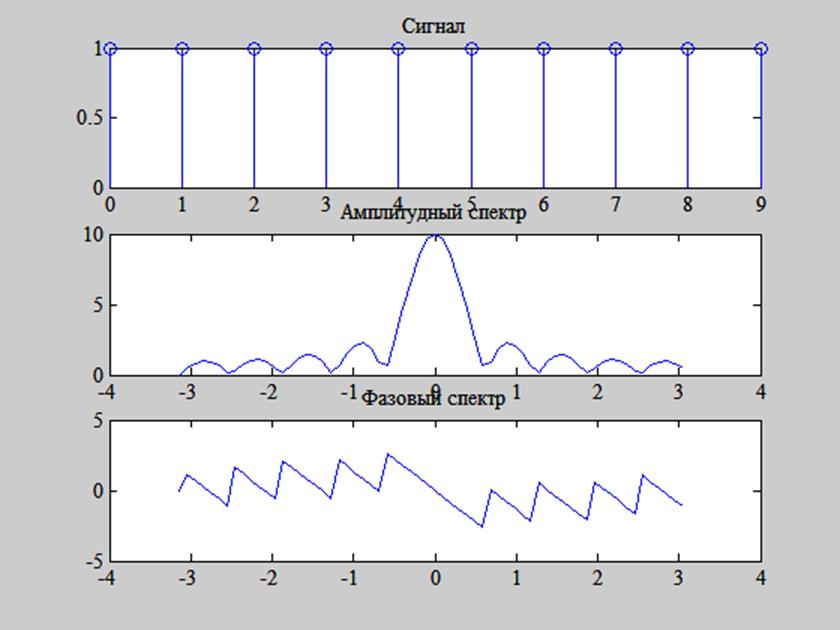
Рис.
2. График сигнала ![]() и его амплитудного и
фазового спектров.
и его амплитудного и
фазового спектров.
Видим, что
спектры дискретного сигнала ![]() непрерывны.
График амплитудного спектра сигнала обладает чётной симметрией, а фазового
спектра – нечётной.
непрерывны.
График амплитудного спектра сигнала обладает чётной симметрией, а фазового
спектра – нечётной.
в) 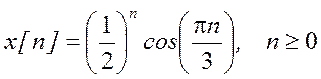
Для определения ДВПФ сигнала и построения графиков его амплитудного и фазового спектров воспользуемся следующим script-файлом.
n=0:1:15;
x=((1/2).^n).*cos((pi/3).*n);
[X,w]=DTFT(x,64)
subplot(3,1,1);
stem(n,x);
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Cигнал');
subplot(3,1,2);
plot(w,abs(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Амплитудный спектр');
subplot(3,1,3);
plot(w,angle(X))
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
title('Фазовый спектр');
Результат представлен на рис. 3.
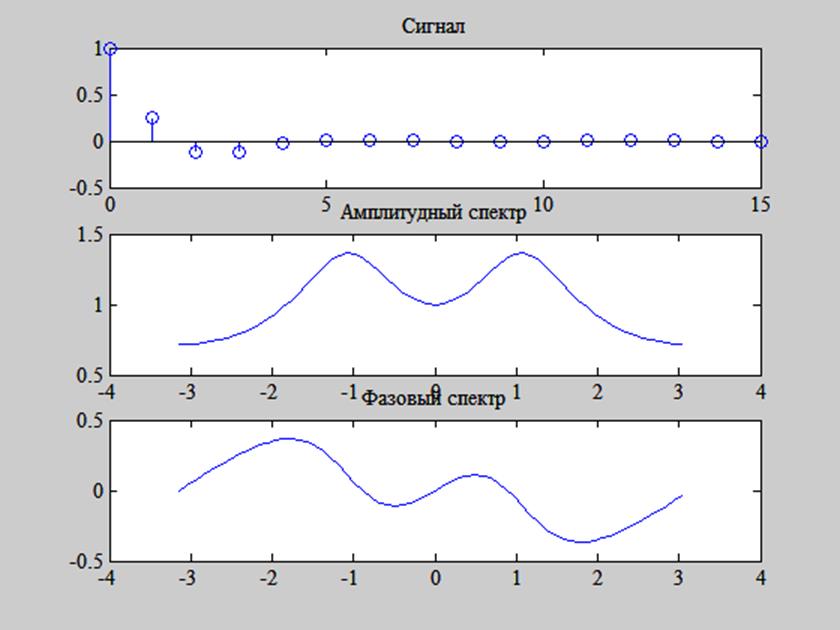
Рис.
3. График сигнала ![]() и его амплитудного и
фазового спектров.
и его амплитудного и
фазового спектров.
Видим, что
спектры дискретного сигнала ![]() непрерывны.
График амплитудного спектра сигнала обладает чётной симметрией, а фазового
спектра – нечётной.
непрерывны.
График амплитудного спектра сигнала обладает чётной симметрией, а фазового
спектра – нечётной.
8. Изучение свойств ДВПФ.
C помощью следующего script-файла определим сигналы h[k] и g[k], построим их графики, а также графики амплитудных спектров данных сигналов.
N = 128; % Длина сигналов
k = 0:N-1;
gamma = -0.1;
g = exp(gamma*k);
% g - экспоненциальная функция
h = sin(2*pi*k/(N/4));
figure(1)
subplot(211),stem(k,g)
title('График сигнала g[k] = exp(gamma*k)')
subplot(212),stem(k,h)
title('График сигнала h[k] = sin(2*pi*k/(N/4))')
% h - синусоидальная последовательность с периодом = N/4
% вычисление ДВПФ
[G,w] = DTFT(g,512);
[H,w] = DTFT(h,512);
figure(2)
subplot(211), plot(w,abs(G))
title('Амплитудный спектр сигнала g[k] = exp(gamma*k)')
subplot(212), plot(w,abs(H))
title('Амплитудный спектр сигнала h[k] = sin(2*pi*k/(N/4))')
Результат представлен на рис. 4 и 5.
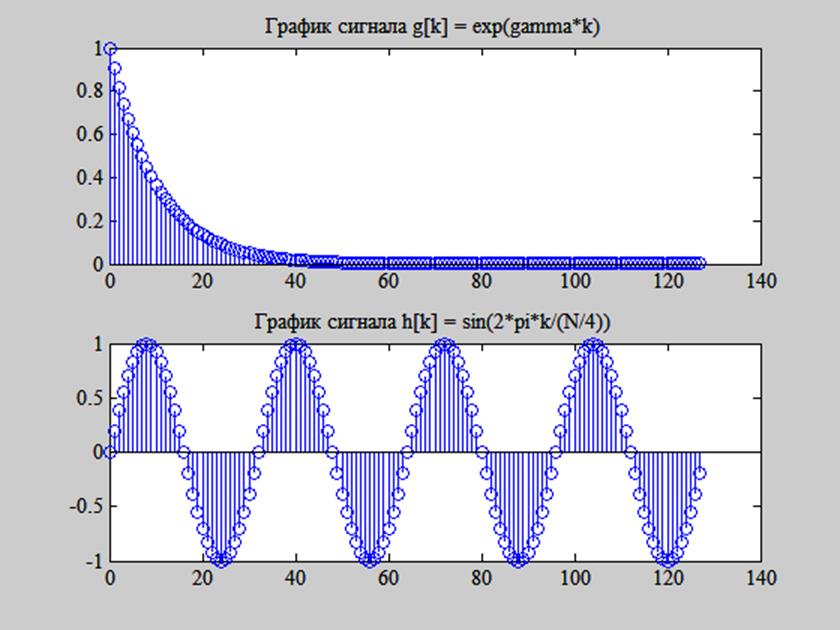
Рис. 4. Графики исходных сигналов h[k] и g[k].
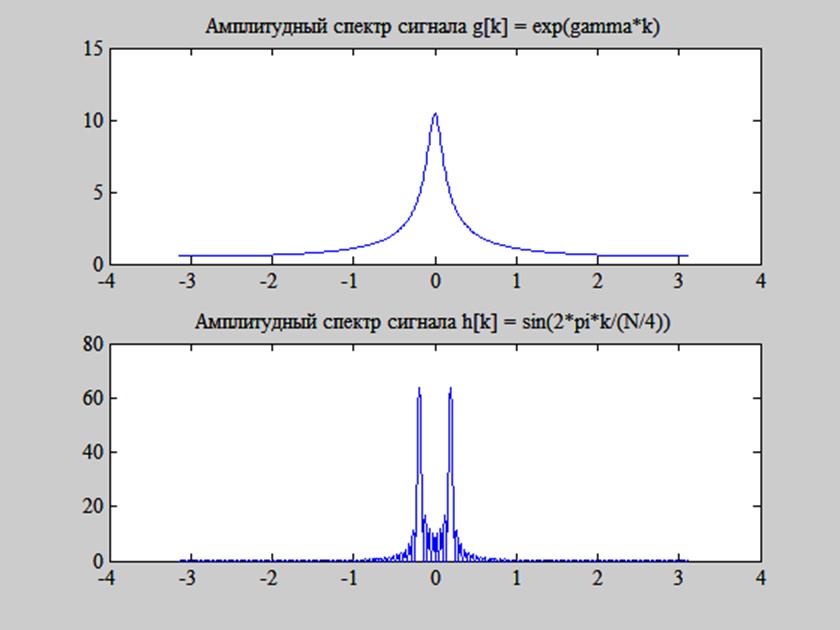
Рис. 5. Графики амплитудных спектров сигналов h[k] и g[k].
8.1. Свойство линейности.
Если ![]() и
и ![]() ,
то
,
то
![]() .
(26)
.
(26)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.