Дискретизация и восстановление сигналов. Вариант 1, страница 2

5)  Используя функцию chirp(), сформировать сигнал с линейно изменяющейся частотой (метод ‘linear’)  длительностью 10 с, частотой отсчетов 8192 Гц, начальным значением частоты 1000 Гц, значением частоты 4000 Гц через 3 с.  С помощью команды sound() прослушать звучание сигнала,  при этом определить с точностью до секунды моменты времени,  в которые тон сигнала понижается или повышается.  Аналитически вычислите моменты времени, в которые тон звука начинает понижаться или повышаться. Сравните их с экспериментальными результатами. Используя процедуру specgram, построить спектрограмму сигнала.  Объяснить на основе теоремы отсчетов и спектрограммы  частотно-временной характер звукового сигнала.

Далее представлен М-файл с помощью которого было прослушано звучание сигнала и построена спектрограмма сигнала.

t=0:1/8192:10;

y=chirp(t,1000,3,4000);

specgram(y,[],8192);

sound(y);

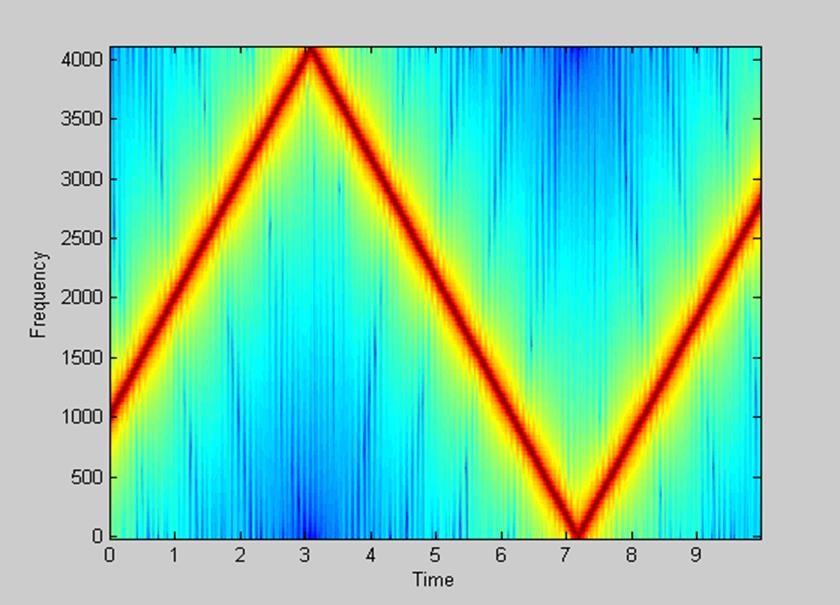
Рис.11. Спектрограмма сигнала

Согласно линейному закону изменения частоты:

,  где   .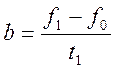

В данном примере , ,    =>   . Тое есть с каждым приращением времени на 1 сек. частота должна увеличиться на 1000 Гц. Однако в результате эксперимента получается расхождение. Это объясняется тем что не учтена частота дискретизации. Спектрограмма показывает зависимость мгновенного амплитудного спектра сигнала от времени. Тое есть max частота показанная на спектрограмме должна равняться 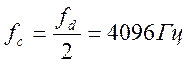, а далее изменение частоты происходит по формуле: , где  (т.е. время когда значение частоты достигло 0 или 4000Гц), , ,   =>  до тех пор пока значение  не станет равным нулю. Потом закон изменения подчиняется снова формуле:

, где , , , .

Получается, что тон сигнала повышается на интервале от 0 до 3.096 сек., далее понижается от 3.096 до 7.192 сек. и потом тон повышается от 7.192 до 10 сек.

Из всего выше сказанного можно сделать вывод:

Так как весь исходный спектр свернулся в полосу частот от 0 Гц до частоты Найквиста (то есть произошло удаление всех ложных частот, т.е. частот выше частоты Найквиста), то расширение спектра происходит дублированием спектра из полосы от 0 Гц до частоты Найквиста. В конечном итоге, спектр дискретизированного сигнала представляет собой несколько копий спектров, полученных в результате отображения относительно оси t и сдвигом по этой же оси на 4.096 сек..

6)  С помощью процедур Приложения 4 провести моделирование восстановления непрерывного сигнала по его отсчетам с использованием трех интерполяционных полиномов. Сделать необходимые комментарии  и выводы об особенностях восстановления сигналов различными методами и их сравнительное сопоставление.

Восстановление непрерывных сигналов по отсчетам с помощью идеального ФНЧ

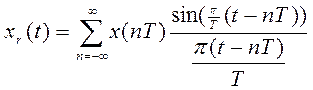
Восстановление аналогового сигнала с помощью интерполяционных полиномов нулевого  и первого порядков

Нулевой порядок :

Первый порядок:

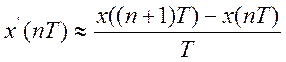- интерполирование вперед

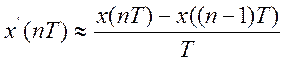- интерполирование назад

Далее представлены М-файлы (основанные на Приложении 4) с помощью которого было смоделировано восстановление непрерывного сигнала по его отсчетам и построены графики.

% Программа демонстрации восстановления сигнала

% интерполяционным полиномом sin(x)/x

% вариант интерполяции с помощью идеального ФНЧ

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0];% дискретный сигнал

d=[n'  s']; % параметры для функции pulstran

y=pulstran(t,d,'sinc');

% график дискретного сигнала

plot(n, s,'o',t,y)

hold on

% построение графиков отдельных sinc импульсов

for k=1:length(s), plot(t, s(k)*sinc(t-n(k)), ':'), end

grid

hold off

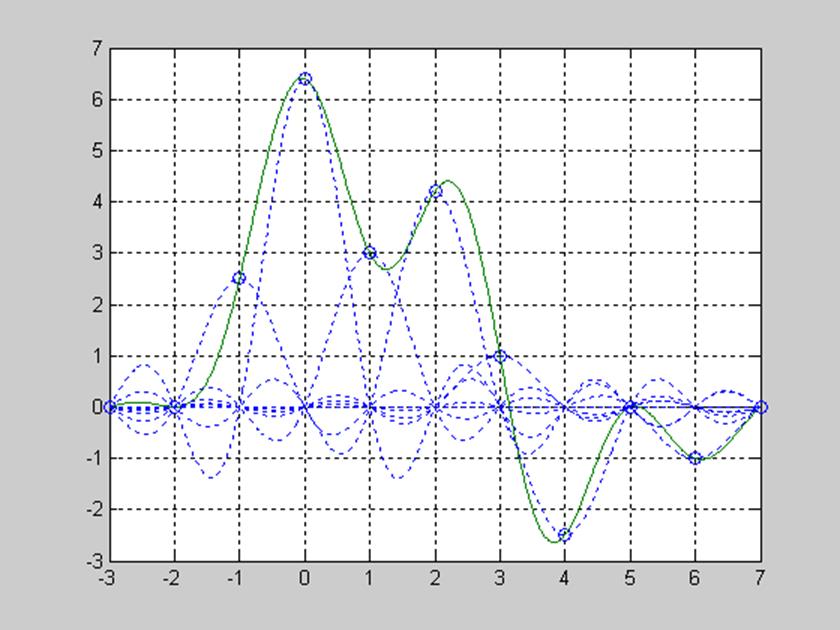
Рис.12. Графическое изображение восстановление дискретного сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0] интерполяционным полиномом sin(x)/x

% Программа демонстрации восстановления сигнала

% с помощью интерполяционного полинома нулевого порядка

%

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0]; % дискретный сигнал

d=[n' s'];  % параметры для функции pulstran

% сигнал,восстановленный полиномом нулевого порядка

y=pulstran(t,d,'rectpuls');

plot(n, s,'o', t, y)  % графики  сигналов

hold on

% сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

% построение графиков отдельных прямоугольных импульсов

for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'), end

hold off

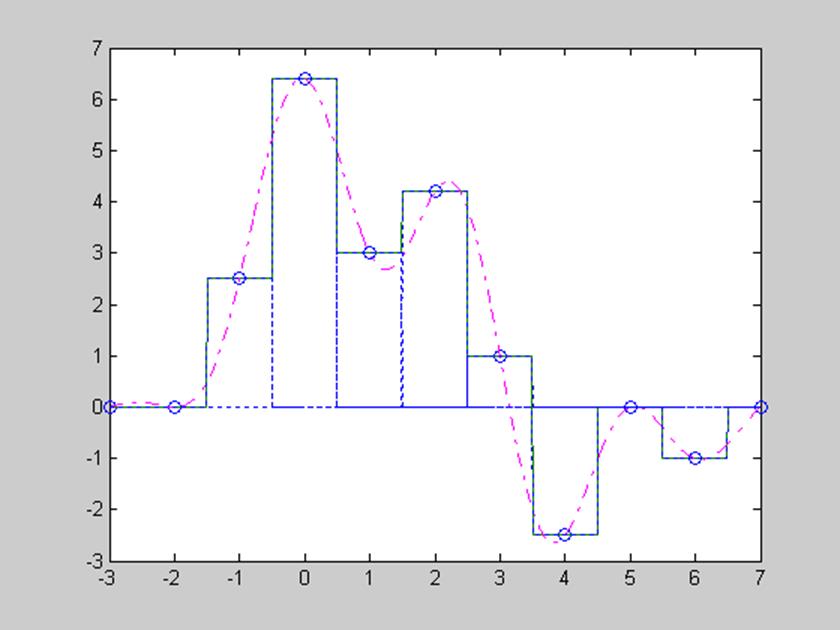
Рис.13. Графическое изображение восстановление дискретного сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0] с использованием интерполяционного полинома

нулевого порядка

% Программа демонстрации восстановления сигнала

% с помощью интерполяционного полинома первого порядка

%

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

% дискретный сигнал

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0];

d=[n' s']; % параметры для функции pulstran

tau=2;  % длительность треугольного сигнала

% сигнал,восстановленный полиномом первого порядка

y=pulstran(t,d,'tripuls',tau);

plot(n, s,'o', t, y) % график восстановленного сигнала

hold on

%сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

hold off

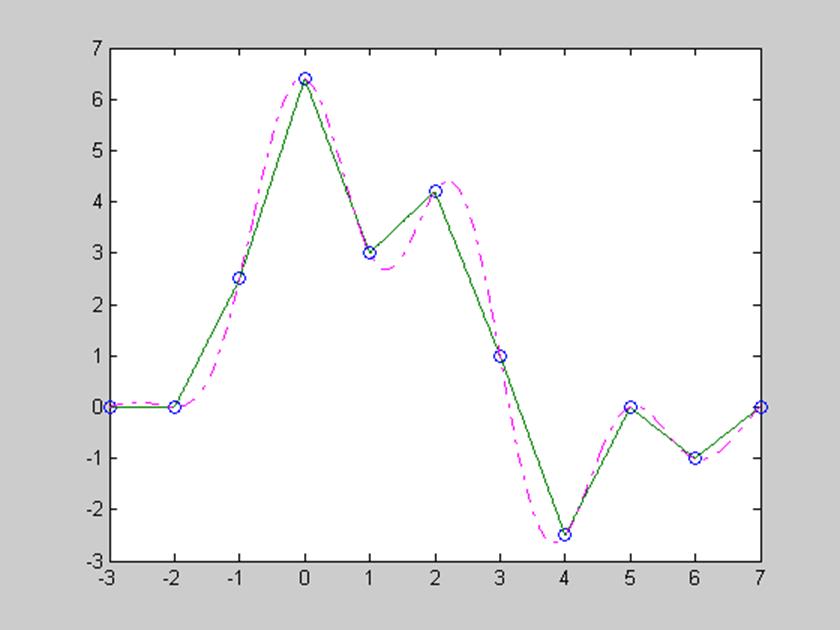
Рис.14. Графическое изображение восстановление дискретного сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0] с использованием интерполяционного полинома

первого порядка

% Программа демонстрации восстановления сигнала

% с помощью интерполяционного полинома нулевого порядка и ФНЧ,

% используемого для сглаживания восстановленного сигнала

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0]; % дискретный сигнал

d=[n' s']; % параметры для функции pulstran

% сигнал,восстановленный полиномом нулевого порядка

y=pulstran(t,d,'rectpuls');

% фильтрация восстановленного сигнала

[b,a]=butter(6,2*pi*0.5,'s'); % получение характеристик фильтра

% Баттерворта

lsim(b,a,y,t); %  фильтрация и построение графика после фильтрации

hold on; axis([-3,8,-4,8])

plot(n, s,'o', t, y) % график восстановленного сигнала

hold on

% сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

% построение графиков отдельных прямоугольных импульсов

for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'), end

hold off

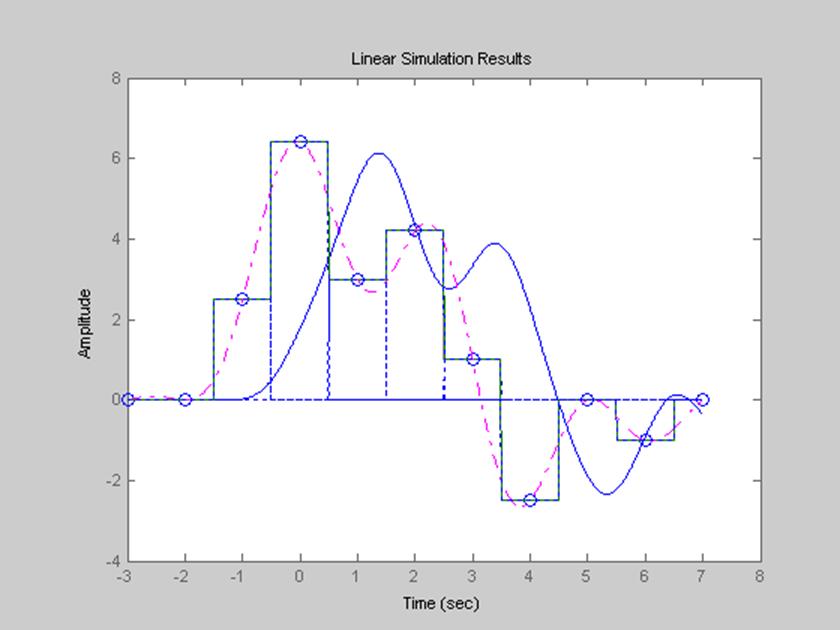
Рис.15. Графическое изображение восстановление дискретного сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0] с использованием интерполяционного полинома

нулевого порядка и ФНЧ

Наиболее эффективным оказался метод с использованием интерполяционного полинома sin(x)/x. График после интерполятора оказался более приближенный к реальному.

Но этот метод мало применим на практике, из-за больших объемов вычисления по формуле интерполяционного ряда Котельникова-Шеннона: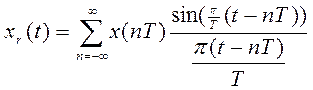 

Методы восстановления сигнала с использованием интерполяционного полинома первого и второго порядка чаще всего применяются на практике. Используя метод интерполяционного полинома нулевого порядка на выходе будет сигнал имеет ступенчатый вид, а  используя метод интерполяционного полинома первого порядка – более гладкий. На практике чаще используется  метод интерполяционного полинома нулевого порядка, т.к. в другом методе нужно вычислять еще и производную.

При пропускании восстановленного сигнала методом интерполяционного полинома первого порядка через ФНЧ, заметно по графику «отставание» сигнала от исходного.