Проектирование широкополосной зеркальной антенны со спиральным облучателем, страница 2

Спиральные антенны относятся к классу антенн бегущей волны. Они представляют собой металлическую спираль, питаемую обычно коаксиальной линией. Существуют различные виды спиральных антенн - цилиндрические, конические, плоские и т.д. В данной курсовой работе рассматривается цилиндрическая спираль.

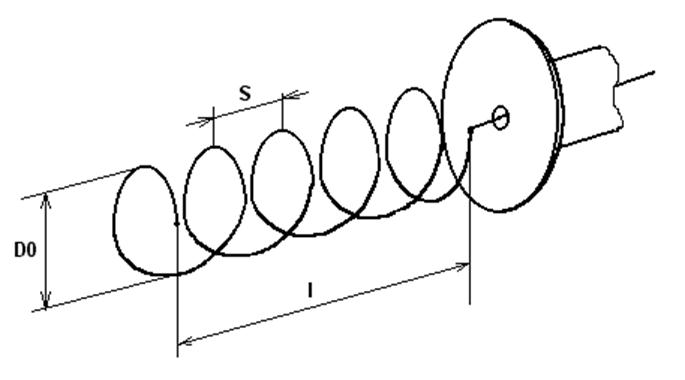
Рис. 1. Цилиндрическая спиральная антенна.

Итак, антенна представляет собой цилиндрическую спираль из провода или металлической трубки (рис.1). Один конец спирали присоединяется к внутреннему проводнику коаксиального кабеля, через трансформатор, согласующий входное сопротивление спирали с сопротивлением кабеля. Поскольку, наибольший практический интерес представляет режим осевого излучения, (антенна излучает максимально вдоль оси), то входное сопротивление спирали, с учетом того, что отношение  длины витка к длине волны тока, бегущей по проводу спирали   равно:

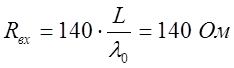, следовательно .

Волновое сопротивление выбранного коаксиального кабеля, тогда сопротивление трансформации, согласующего трансформатора :

.

Наружная оболочка кабеля соединена с металлическим экраном диаметром порядка .

Приведем основные обозначения для цилиндрической спирали (рис.1):

- осевая длина спирали.

 - шаг спирали.

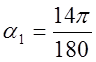 - угол намотки.

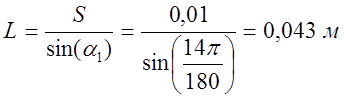 - длина витка.

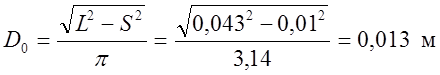  - диаметр.

Для нахождения числа витков N, используя амплитудную ДН для спиральной антенны:

Волновое число: .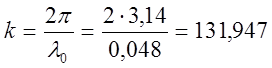

Угол облучения: .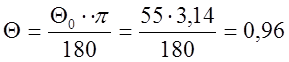

Угол в пространственной системе координат: .

Приравняв 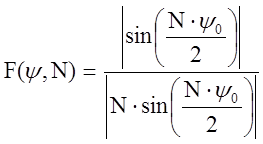  и  решим трансцендентное уравнение, при  определим количество витков N.

         

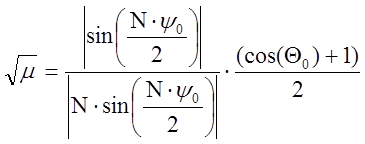
Заметим, что здесь   это не угол облучения как говорилось выше, а величина, выраженная через :

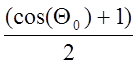  следует из нормировки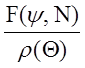

где, 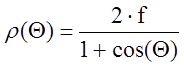 - профиль зеркала.

Решение уравнения  можно провести следующим образом. Вводя обозначение   и перенося все известные величины в правую часть, получим уравнение:

.

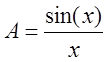
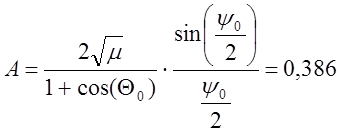Вычисляя A, корень из этого уравнения  x, используя таблицы функции 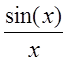,  легко определим N, по формуле 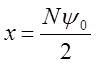. Число витков N=7,245.

Зная число витков спирали, можно построить график ДН данной спиральной антенны по следующей формуле:

,

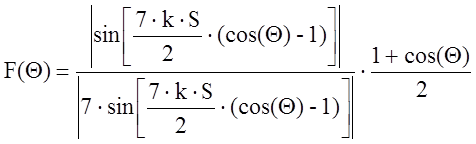Которая следует из 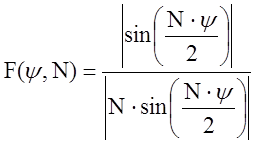 путем нормировки   и подстановки N=7.

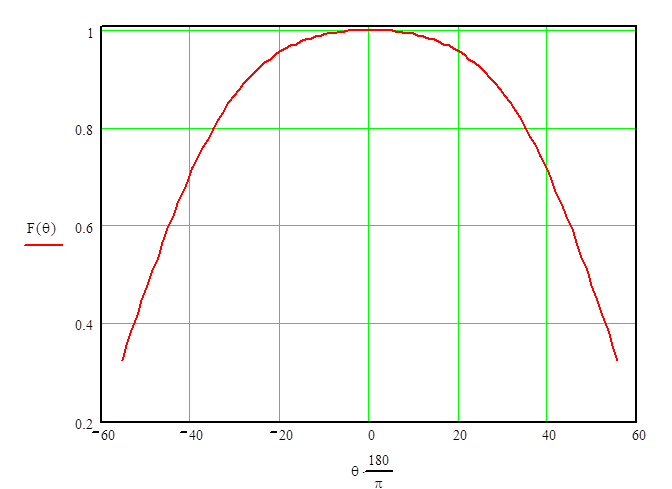
Рис. 2. Диаграмма направленности спирального облучателя.

7.  Нахождение распределения поля в раскрыве зеркала.

Распределение поля в апертуре зеркала зависит от координаты r, то есть  .  Для удобства заменим r  безразмерной переменной 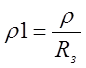, которая на краю зеркала обращается в единицу. Связь между координатами r и q определяется выражением:

,

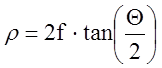тогда безразмерная величина: .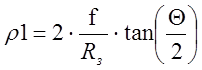

График распределения поля в апертуре зеркала представлен на Рис. 3. Заметим, что   это не что иное, как  с пересчитанной осью абсцисс   в .

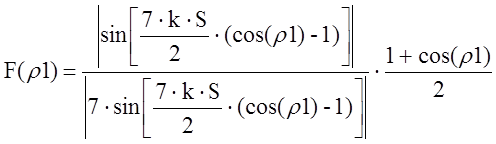
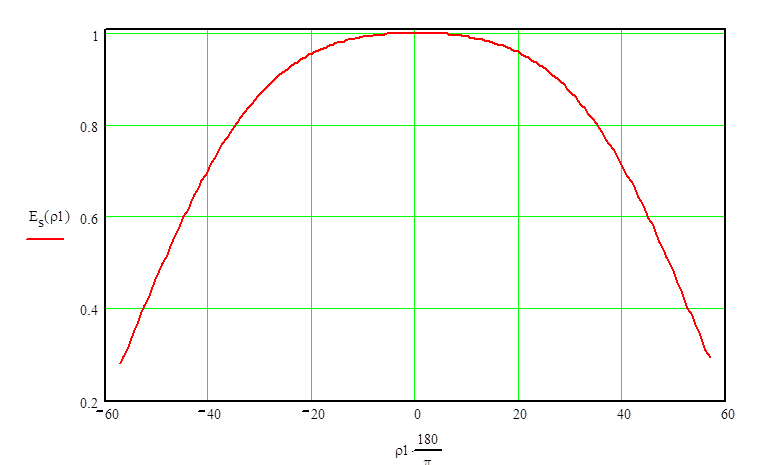
Рис. 3. График распределения поля в апертуре зеркала.

8.   Нахождение параметров аппроксимирующего выражения .

Аппроксимация распределения поля по апертуре принимается в форме:

                                             (*)

где  при.

D - параметр, учитывающий случайные отклонения от идеальной параболы зеркала.

Можно заметить, что при  функции  и  совпадают.  Целесообразно уравнять их так же при . При этом определяется параметр :

 при

тогда: .

Остается выбрать второй параметр аппроксимирующего выражения (*) - показатель степени . Для этого построим графики функций (*) при различных  значениях  и сравним их с графиком функции распределения .

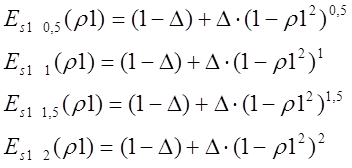
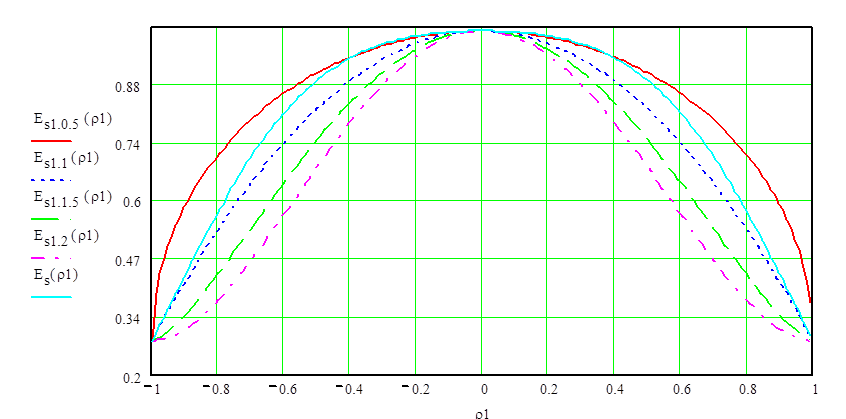
Рис. 4. График аппроксимирующих поля в апертуре зеркала.

Как видно из графиков на Рис.4  наиболее точно функцию повторяет  при .

9.  Расчет нормированной ДН антенны в области малых углов и нахождение диаметра зеркала.

Зная параметры аппроксимирующего выражения , то есть D и r, по формуле:

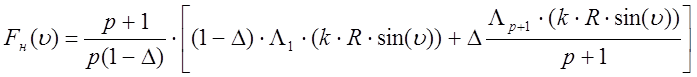
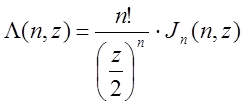 - ламбда функция n-ого порядка.

Нормированная ДН антенны в области малых углов (параметр z):

.

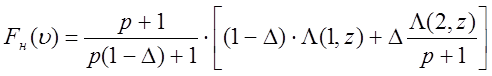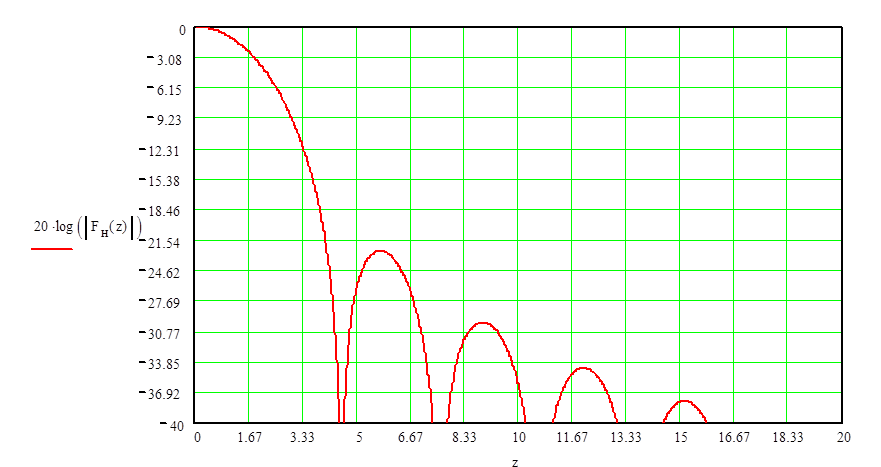
Рис.5. Нормированная ДН антенны в области малых углов (параметр z).

Нормированная ДН антенны в области малых углов (параметр):

 

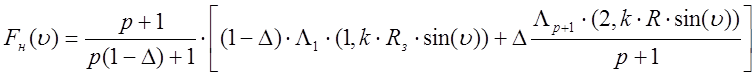
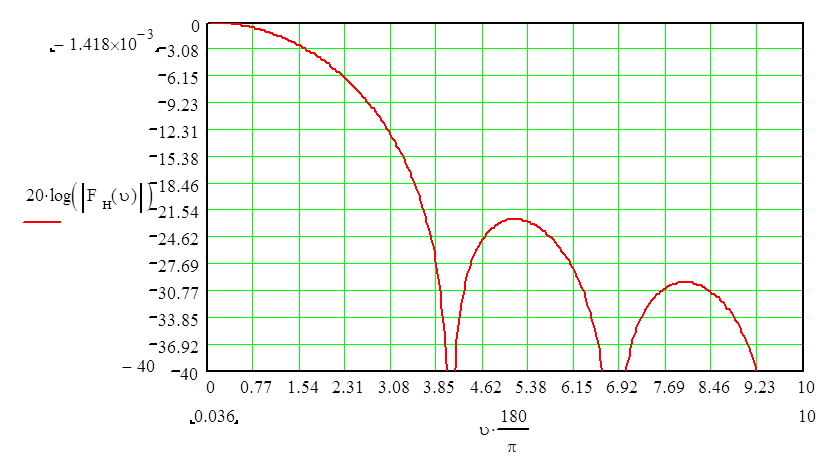
Рис.6. Нормированная ДН антенны в области малых углов (параметр ).

Имея в распределении график ДН в функции z, можно определить ширину главного лепестка в обеих главных плоскостях , на уровне 0,707  (-3дБ) по полю. Для этого  по графику Рис.5. определим значение координаты z₀, при которой уровень диаграммы равен -3дБ. Зная z₀, и R_з, легко найти :

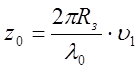 или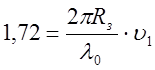

                             

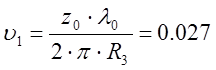
Тогда ширина главного лепестка диаграммы:

.

Переведя в градусы, получим:

Диаметр зеркала:

.

10. Вычисление параметров антенны.

После расчета нормированной ДН не трудно определить два важных параметра антенны: коэффициент расширения луча и максимальный уровень боковых лепестков (УБЛ) диаграммы направленности.

       Коэффициент расширения луча:

.

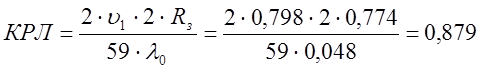Максимальный уровень боковых лепестков определим из графика Рис.5. Максимальный УБЛ представляет собой максимальный уровень бокового лепестка относительно максимума основного лепестка, выраженный в децибелах:

.

Апертурный коэффициент использования площади:

.

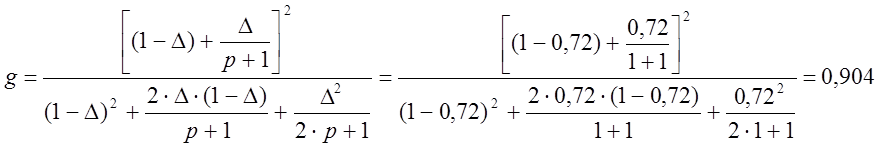11. Построение профиля зеркала.

Профиль зеркала строится в осях (x,z1) по формуле:

.

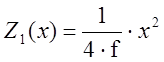График функции z1(x) изображен на Рис.7. Точка С на графике - фокус зеркала.

 

Рис. 7. Профиль Зеркала.

12. ВЫВОДЫ:

      По проделанной работе - расчету зеркальной антенны со спиральным облучателем можно сказать следующее. Выбранная в соответствии с рабочей частотой, линия передачи (коаксиальный кабель) с конечным значением затухания a =0.4 дБ/м дает довольно не плохой КПД который составляет 96%, что говорит о том, что практически вся подводимая к антенне мощность идет на излучение. Радиус зеркала, так же рассчитанный в соответствии с заданной частотой (длинной волны) и шириной ДН составляет 0,774м. Значения КИП, апертурного КИП, КНД и коэффициента усиления антенны рассчитанные в разделе - 4, получились достаточно большими и не противоречат требованиям технического задания: КИП  Ku=0.678, апертурный КИП g=0.904, КНД D=7071, коэффициент усиления G=5021.

       Число витков спирали играющей роль облучателя зеркальной антенны, при выбранном угле облучения y₀=55⁰ , составляет 7, что не превосходит верхнего предела числа витков N и не меньше нижнего предела. Уровень облучения края зеркала при этом, составляет 0.316 (-10дБ).

       Полученное в разделе 6 распределение поля в апертуре зеркала, при r1=1 (r=Rз), как и должно быть составляет 0.316.

       В качестве аппроксимирующего выражения для Еs(r1) (распределение поля в апертуре зеркала) выбрано Еs1(r1)  при параметре p=1, так как именно при этом значении p, аппроксимирующая функция наиболее точно повторяет Еs(r1) (Рис.4).

       Ширина главного лепестка нормированной ДН в области малых углов (Рис.6), полученной в разделе - 8, составляет 1.60 по уровню -3дБ, что совпадает с заданным значением ширины ДН  в задании на курсовую работу.