Если какие-либо k юношей знакомы меньше чем с k девушками, то очевидно, их нельзя поженить.
Достаточность:
Проведем индукцию по числу юношей.
1. База индукции: m = 1, b1 → g1
2. Пусть теорема верна для m-1 юношей.
3. Возможно два следующих варианта:
1) Любые k юношей 1 ≤ k < m знакомы, по крайней мере с k+1 девушкой. Возьмём любого юношу и женим на любой знакомой ему девушке, тогда для других m-1 юношей условие теоремы справедливо, т.е. любые k юношей знакомы с k девушками. По индукционному предположению остальных юношей можем поженить так как надо.
2) Пусть данные k юноши знакомы ровно с k девушками, а так как k<m то по индукционному предположению этих k юношей мы можем поженить. Осталось m-k юношей, причем любые h из них знакомы по крайней мере с h девушками 1 ≤ h≤ m-k, а так как k≥1, то h<m и по индукционному предположению этих оставшихся m-k юношей мы можем поженить.
Билет №24. Деревья и леса. Основная теорема о деревьях и её следствия.
Деревом называется граф G, если он является связным и не имеет циклов.
Лес - это граф G, все компоненты, связности которого являются деревьями.
Следующие утверждения эквивалентны:
Следующие утверждения эквивалентны:
1. Граф Т – дерево;
2. В графе Т любые две вершины x и связаны одним путем (цепью)
3. Т – минимальный связный граф, т.е. для любого ребра е![]() Т граф Т без е несвязен.
Т граф Т без е несвязен.
4. Т – минимальный ациклический граф, т.е. в графе Т нет циклов, а для любых смежных вершин x,y в графе Т+xy есть цикл x,y.
Граф ![]() называется остовным для графа
называется остовным для графа ![]() , если
, если ![]() .
Если
.
Если ![]() - дерево, то
- дерево, то ![]() называется
остовным деревом.
называется
остовным деревом.
Следствие 1:
В связном графе минимальный связный остовный подграф является деревом. В частности любой остовный граф обладает остовным деревом.
Следствие 2:
Связный граф на n вершинах является деревом тогда и только тогда, когда он имеет (n-1) ребро.
Доказательство:
Необходимость:
Пусть граф G – дерево на n вершинах с m ребрами. Покажем, что m=n-1. проведем индукцию по n.
Удалим
один лист из G, получим дерево ![]() на
n-1 вершине. По индукционному предположению в
на
n-1 вершине. По индукционному предположению в ![]() n-2 ребра. С
другой стороны в графе
n-2 ребра. С
другой стороны в графе ![]() (m-1)
ребро
(m-1)
ребро ![]() m-1=n-2
m-1=n-2 ![]() m=n-1
m=n-1
Достаточность:
Пусть в графе G n-1 ребро. Покажем, что G дерево. В силу следствия (1) в G
существует остовное дерево Т. в силу доказанной необходимости в Т (n-1) ребро ![]() Т=G
Т=G ![]() G дерево.
G дерево.
Выделенная вершина в дереве называется корнем. В качестве корня можно выбрать любую вершину. Выбор корня в дереве задает на множестве его вершин частичный порядок, т.е. бинарное отношение, которое рефлексивно, антисимметрично и транзитивно.
По определению для x,y ![]() V(Т),
V(Т), ![]() , если
, если ![]() ,
где rTy – путь с началом r и
концом y.
,
где rTy – путь с началом r и
концом y.
1.рефлексивность ![]()
2. антисимметричность
пусть ![]()
![]()
![]() x=y
x=y
3. транзитивность.
Пусть ![]()
![]()
Введены порядок называется древесным порядком на дереве Т. Он зависит от выбора корня.
Свойства древесного порядка:
Билет №25, №27. Критерий двудольности графа и его следствие.
Граф G=(V,E) называется двудольным графом, если множество его вершин можно разбить на два непересекающихся множества V1 и V2 (V1 ∩ V2=Ø, а V1 U V2 = V) таким образом, что в V1 никакие две вершины не связаны между собой, аналогично в V2.
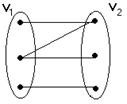
Граф называется полным двудольным графом, если каждая вершина из V1 соединена с каждой вершиной V2.
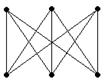
Теорема.
Граф является двудольным, тогда и только тогда, когда длины всех его простых циклов четны.
Доказательство:
 Необходимость:
Необходимость:
Вершины одного класса не должны быть смежны.
Достаточность:
Пусть G=(V,E) не содержит нечетных циклов.
Очевидно, что если все компоненты связанности графа G являются двудольными или тривиальными графами, т.е.
изолированными точками, то сам граф G будет двудольным.
Таким образом можно считать, что граф G связен. Пусть Т
– остовое дерево в G. Для любой вершины ![]() единственная цепь
единственная цепь ![]() имеет либо нечетную, либо четную
длину. Это
имеет либо нечетную, либо четную
длину. Это ![]() задает разбиение множества V. Покажем, что это разбиение делает наш граф двудольным,
т.е. внутри этих разбиений вершины не инцидентны.
задает разбиение множества V. Покажем, что это разбиение делает наш граф двудольным,
т.е. внутри этих разбиений вершины не инцидентны.
Пусть е=xy - ребро графа G. Возможны два варианта:
1. ![]() .
Тогда rTy=rTxy
.
Тогда rTy=rTxy
![]() x и y лежат в разных разбиениях.
x и y лежат в разных разбиениях.
2. ![]() x и y инцидентны в T.
x и y инцидентны в T.
Граф содержит цикл xTy+е, который имеет четную длину. А чикл четной длины всегда можно сделать двудольным графом.

Следствие:
Любой лес, в частности дерево, является двудольным графом.
Билет №26. Лемма о рукопожатиях и её следствие. Регулярные графы.
Число ребер инцидентных данной вершине v называется степенью этой вершины d(v)
Лемма о рукопожатии
Сумма
степеней всех вершин v Î V равна удвоенному числу
ребер ![]()
Доказательство:
Следует из анализа матрицы инцидентности, в которой сумма элементов любого столбца равна двум.
|
е1 |
е2 |
е3 |
е4 |
е5 |
|
|
1 |
1 |
0 |
0 |
0 |
1 |
|
2 |
1 |
1 |
0 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
1 |

т.к. число столбцов равно числу ребер, а сумма элементов в каждом столбце =2, а все число единиц в матрице = сумме степеней вершин.
Следствие:
 Число вершин нечетной степени чётно в
любом графе
Число вершин нечетной степени чётно в
любом графе
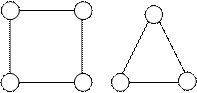
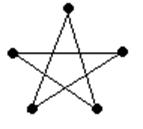
Граф называется регулярным (n-регулярным) если степени его вершин совпадают (равны n).
Билет № 28. Лемма о числе ребер в полном графе.
Лемма
Число
ребер в полном графе на n вершинах равно 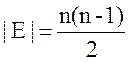
Доказательство:ъ
Проведем индукцию по n ;
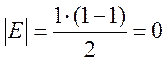
2. Шаг индукции: Выбираем из графа G одну вершину и все ребра ей инцидентные. Очевидно, мы получим полный граф на n-1 вершине.
По индукционному предположению: |E(Kn-1)|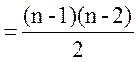
Ранее мы выбросили n-1 ребро =>
|E(Kn)| =
= 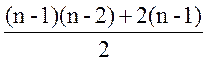
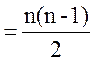
Kn – полный граф.
Билет №29. Выборки и отображения. Три теоремы о числе функциональных отображений.
Пусть ![]() -
множество всех отображений (функций).
-
множество всех отображений (функций). ![]()
Теорема 1.
Пусть ![]() ;
;
Тогда ![]()
Доказательство:
Пусть ![]() тогда
любое отображение
тогда
любое отображение![]() можно представить в виде
упорядоченной последовательности
можно представить в виде
упорядоченной последовательности ![]() значений функций
f в точках из Х, где
значений функций
f в точках из Х, где ![]() .
Очевидно, что мы тем самым установили взаимнооднозначное соответствие между
множеством функциональных отображений и множеством упорядоченных выборок с
повторениями объема r из множества y
объема n, откуда и следует справедливость доказываемого
утверждения. тогда f есть вектор
.
Очевидно, что мы тем самым установили взаимнооднозначное соответствие между
множеством функциональных отображений и множеством упорядоченных выборок с
повторениями объема r из множества y
объема n, откуда и следует справедливость доказываемого
утверждения. тогда f есть вектор ![]() .
.
Теорема 2.
Пусть ![]() ;
;
Тогда число всех инъективных
отношений из x в y равно 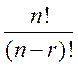 .
.
Доказательство:
Пусть ![]() ,
тогда любой инъекции
,
тогда любой инъекции ![]() соответствует вектор
соответствует вектор ![]() ;
;
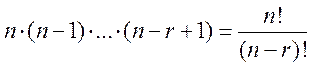
Теорема 3.
Пусть ![]() , тогда число всех биекций равно n!
, тогда число всех биекций равно n!
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.