Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 6

                                                                                                         

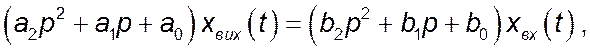
де p – оператор диференціювання, ;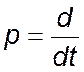

 – сигнал на вході ланки;

 – сигнал на виході ланки;

, , ,    – сталі коефіцієнти.

Зображення за Лапласом лінійного диференціального рівняння в операційній формі (при нульових початкових умовах) має вигляд:

                                                                               

або

                                                                                                    

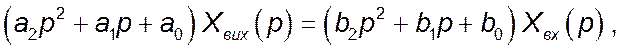
де p – оператор Лапласа;

 – зображення за Лапласом сигналу на вході ланки;

 – зображення за Лапласом сигналу на виході ланки.

Функція передачі ланки другого порядку:

                                                 

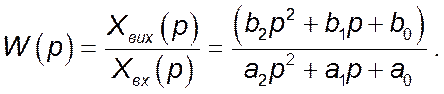
Як правило, рівняння динаміки в операційній формі прийнято приводити до нормованого вигляду:

                                                                                             

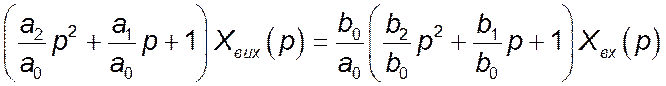
або

                                                                                              

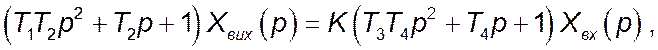
де K – сталий коефіцієнт (коефіцієнт передачі), ;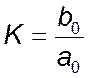

, , , – сталі коефіцієнти, , , , .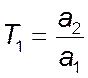

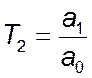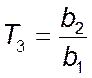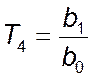Розмірність коефіцієнта K залежить від розмірностей сигналів  і . При однакових розмірностях сигналів  і  коефіцієнт K є безрозмірним, а інші коефіцієнти , , ,  мають розмірність часу.

Лінійним динамічним ланкам прийнято давати назви в залежності від виду лівої і правої частин рівнянь динаміки.

Для наведених нижче ланок ліва частина рівняння динаміки має наступний вигляд:

- ідеальна ланка (, ):

                                                                                       

- аперіодична ланка першого порядку (, ):

                                                                       

- аперіодична ланка другого порядку (, , ):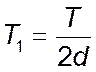

                                                    

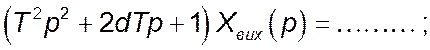
- коливальна ланка (, , ):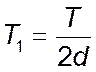

                                            

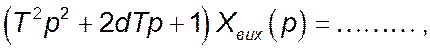
де показник (декремент) затухання.

З наведеного випливає, що останні дві ланки (аперіодична та коливальна) є ланками другого порядку і мають однакові на вигляд рівняння динаміки, а отже однакові на вигляд функції передачі. Різницю ланок обумовлює числове значення декременту затухання d.

Якщо d≥1, то корені характеристичного рівняння будуть дійсними, в перехідному процесі такої ланки відсутня коливальна складова, перехідний процес має монотонний характер. Така типова динамічна ланка називається аперіодичною (інерційною) ланкою другого порядку.

Якщо 0<d<1, то корені характеристичного рівняння будуть комплексними спряженими, в такому випадку перехідний процес матиме коливальний характер. Така типова динамічна ланка має назву коливальної.                                                         

Обидві розглянуті ланки, якщо виконуються умови  і , є стійкими тому, що в усталеному (статичному) режимі вихідний сигнал  наближається до певного постійного значення. При  або усталений режим неможливий, вихідний сигнал ланки буде коливатися з безперервно зростаючою до нескінченності амплітудою (нестійка ланка), а при  амплітуда коливань стає постійною (ланка на межі стійкості).  

Для наведених нижче ланок права частина рівняння динаміки має наступний вигляд:

- проста ланка:

                                                                                     

- диференціююча ланка:

                                                                                   

- інтегруюча ланка:

                                                                                   

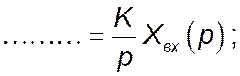
- ланка з введенням похідної:

                                                                     

- ланка з введенням інтеграла:

                                                                   

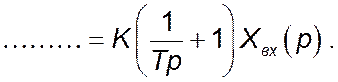
У правій частині рівняння динаміки диференціюючої ланки коефіцієнт K має розмірність часу (наприклад, с). При однакових розмінностях вхідного і вихідного сигналів можна праву частину рівняння динаміки записувати в вигляді

                                                                                    

де .

У правій частині рівняння динаміки інтегруючої ланки коефіцієнт K має розмірність, яка обернена розмірності часу (наприклад, ). При однакових розмінностях вхідного і вихідного сигналів можна праву частину рівняння динаміки можна записувати в вигляді

                                                                                  

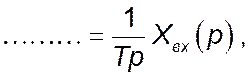
де .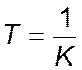

Крім ланок з введенням похідної або інтеграла, можуть бути ланки з більш складною правою частиною, наприклад, з введенням другої похідної.

Як вже було наведено вище, назва ланці дається одночасно в залежності від виду лівої і правої частин рівняння динаміки. Наприклад, ланка, яка описується в операційній формі рівнянням динаміки , має назву аперіодичної диференціюючої ланки.

Динамічні властивості типових динамічних ланок повністю визначаються лінійними диференціальними рівняннями (функціями передачі), які ці ланки описують, якщо відомі всі сталі коефіцієнти. Для розв’язання лінійних диференціальних рівнянь необхідно, по-перше, задати початкові умови, а по-друге, задати закон зміни вхідного сигналу ланок в залежності від часу.

Перехідні (часові) характеристики типових динамічних ланок

Якщо початкові умови нульові і вхідний сигнал  являє собою одиничний стрибок , то аналітична форма відображення характеру зміни вихідного сигналу  в часі має назву перехідної функції (її часто позначають як ), а графічне зображення перехідної функції має назву перехідної характеристики. Є різні способи отримання перехідної функції.

Самий простий спосіб полягає в використанні оберненого перетворення за Лапласом, результати якого беруться із відповідних таблиць перетворення:

                                                                 

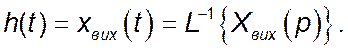
Ще один спосіб полягає в використанні теореми розкладення.