Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 5

Для визначення зображення по Лапласу вихідної величини операційним методом в рівняння

Х_вих(р) = W(p)Х_вх(р)

замість Х_вх(р) треба підставити зображення по Лапласу одиничного стрибка L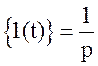 та вираз функції передачі

 .

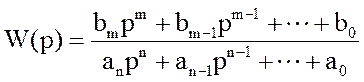Оскільки за визначенням зображення по Лапласу перехідної функції H(p) і є зображення по Лапласу вихідної величини Х_вх(р) при одиничному стрибку, то

.

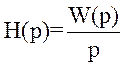Оригінал перехідної функції h(t) можна визначити по відповідним таблицям зворотного перетворення Лапласа або користуючись теоремою розкладення. В останньому випадку послідовність визначення полягає в наступному.

В загальному випадку, при відсутності нульових полюсів, H(p) має вигляд дробно-раціональної функції:

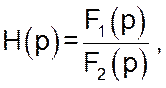
де - чисельник зображення по Лапласу перехідної функції H(p);

     - знаменник зображення по Лапласу перехідної функції H(p).

В такому випадку перехідну функцію  можна визначити за основною формулою теореми розкладення:

                                                           

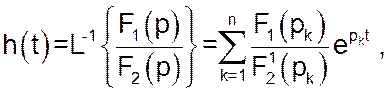
де n – степінь поліному ;

     – корені характеристичного рівняння , ;

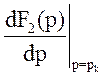=- похідна знаменника зображення по Лапласу перехідної функції H(p).

В випадку однократного нульового полюса зображення за Лапласом перехідної функції має вигляд дробу:

                                                                                             

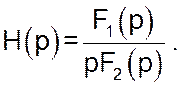
Оригінал перехідної функції  можна визначити за додатковою формулою теореми розкладення:

                                    

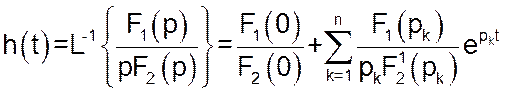
Перехідна характеристика є графічним відображенням перехідної функції h(t) , являючи собою графічне зображення зміни вихідної  величини у часі при одиничній стрибкоподібній зміні вхідної величини.

Окрім перехідної характеристики існує ще імпульсна характеристика. Вона являє собою реакцію елементу або системи керування в цілому на вхідний імпульс необмеженої величини при нульовій його тривалості (δ-функція). Теоретично δ-функція дорівнює похідній одиничного стрибка δ(t)=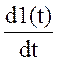, а площа імпульсу дорівнює одиниці, тобто S =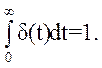 

Аналітичний вираз, по якому будується імпульсна характеристика, називається функцією ваги w(t). Між функцією ваги w(t) і перехідною характеристикою h(t) існує однозначний взаємозв’язок:

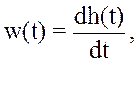
а функція передачі W(p) являє собою пряме перетворення Лапласа функції ваги w(t)

.

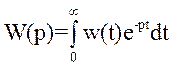Частотні характеристики.

Для оцінки частотних властивостей елементів і систем широко використовуються так звані частотні характеристики.

Розглянемо систему керування, рівняння динаміки якої записано в операторній формі:

а_nрⁿх_вих(t)+ а_n-1р^n-1х_вих(t)+…….+ а₀х_вих(t) = b_mp^mx_вх(t)+ b_m-1p^m-1x_вх(t)+…….+ b₀x_вх(t)

Нехай на вхід системи поданий гармонічний сигнал х_вх(t) = А_вх Sin ωt.

Після закінчення перехідного процесу на виході системи керування встановляться теж гармонічні коливання з тією ж частотою, але з іншою амплітудою і зсунуті по фазі на кут φ відносно вхідного впливу:

х_вих(t) = А_вих sin (ωt+φ(ω)),

де А_вх, А_вих – амплітуди вхідного та вихідного сигналів відповідно;

φ(ω) – кут зсуву по фазі вихідного сигналу, який залежить від частоти вхідного сигналу.

Використаємо комплексну форму запису:

х_вх(t) = А_вх e^jωt;

        х_вих(t) = А_вих e^{(jωt+φ(ω))}.

Підставимо ці значення в операторну форму диференціального рівняння, враховуючі при цьому, що е^{j(ωt+φ(ω))} = е^jωt е^jφ(ω); р^к(А_вхе^jωt) = (jω)^кА_вхе^jωt; р^к(А_вихе^{j(ωt+φ(ω))}) = (jω)^кА_вихе^jωt е^jφ(ω):

(а_n(jω)ⁿ+ а_n-1(jω)^n-1+…….+ а₀) А_вихе^jωt е^jφ(ω) = (b_m(jω)^m+ b_m-1(jω)^m-1+…….+ b₀) А_вхе^jωt

звідки:

.

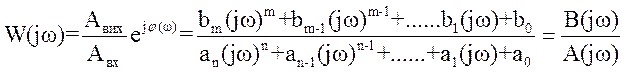
Неважко побачити, що права частина являє собою функцію передачі, в якій зроблена підстановка р = jω. Оскільки ця величина являє собою комплексне число, то його можна записати у вигляді:

W(jω) =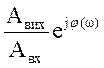

Вираз W(jω) називають комплексним коефіцієнтом передачі, або комплексною функцією передачі. Як кожну комплексну величину, її можна представити або в декартовій, або полярній системі координат.

 Графічне відображення комплексного коефіцієнту передачі комплексній площині називають амплітудно-фазовою частотною характеристикою:

W(jω) = P(ω) + jQ(ω),

де P(ω) – дійсна частина;

     Q(ω) – уявна частина.

Для полярної системи

W(jω) = ,

де А(ω) – коефіцієнт передачі системи на частоті ω, за своєю сутністю є модулем  комплексного коефіцієнта передачі W(jω):

А(ω) == =  ,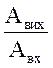

Зсув по фазі φ(ω) є аргументом комплексного коефіцієнту передачі W(jω):

φ(ω) = arg(W(jω)) = arc tg.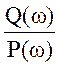

φ(ω)

Графічне зображення залежності коефіцієнта передачі А(ω)  від частоти називається амплітудно-частотною характеристико (АЧХ) , а залежності зсуву по фазі φ(ω)  вихідного сигналу від частоти – фазово-частотною характеристикою (ФЧХ).

Обидві частотні характеристики можна побудувати в логарифмічних координатах. При побудові логарифмічної амплітудно-частотної характеристики (ЛАЧХ) по осі абсцис відкладають логарифм частоти в декадах, а по осі ординат L(ω)= 20 lg A(ω) в децибелах. Для логарифмічної фазово-частотної характеристики (ЛФЧХ) по осі ординат відкладають значення фази в радіанах або в градусах.

lgω, дек

Під декадою розуміють масштабний відрізок на осі, співвідношення частот на кінцях якого дорівнює 10.

В теорії автоматичного керування іноді використовують побудову залежностей дійсної P(ω), а  також уявної Q(ω)  частин комплексного коефіцієнту передачі від частоти, отримуючи таким чином дійсну частотну та уявну частотну характеристики ДЧХ і УЧХ. ДЧХ в свій час була дуже поширена, оскільки являлася основою для побудови перехідних характеристик систем керування завдяки однозначному її зв’язку  з перехідними процесами. З розвитком сучасних засобів обчислювальної техніки та числових методів рішення диференціальних рівнянь використання ДЧХ дещо зменшилося.

Типові динамічні ланки.

Типовою динамічною ланкою називається частина системи автоматичного керування, яка описується лінійним диференціальним рівнянням не вище другого порядку.

Для типової динамічної ланки другого порядку рівняння динаміки в загальному випадку в операторній формі запису має вигляд: