Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 11

Будемо вважати, що на систему керування впливає дія лише завдання Y(p) ( збурення вважають відсутнім, f(p)=0), а вихідною величиною є  координата стану об’єкта керування – Х(р), то за відповідну функцію передачі слід прийняти

,

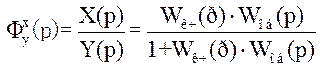яку називають функцією передачі для керованої величини Х(р)  по завданню Y(p). Добуток двох функцій передачі, що входить до означеного виразу являє собою еквівалентну функцію передачі W(p) послідовно з’єднаних керуючої частини і об’єкту керування, тобто розімкненої системи (без урахування від’ємного зворотного зв’язку):

W(p) = W_кч(p)· W_об(p).

Виконавши відповідну підстановку, отримаємо у кінцевому вигляді:

.

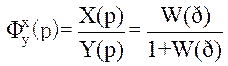Якщо вважати, що на систему керування, як і попередньому випадку, впливає дія лише завдання Y(p), але вихідною величиною є помилка керування ε(р), то відповідну функцію передачі для помилки керування по завданню  визначити неважко:

.

Для визначення функції передачі  для керованої величини Х(р)  по збуренню f(p) структурну схему треба дещо перетворити, виконуючі необхідні правила перетворення:

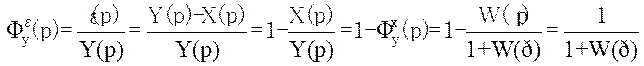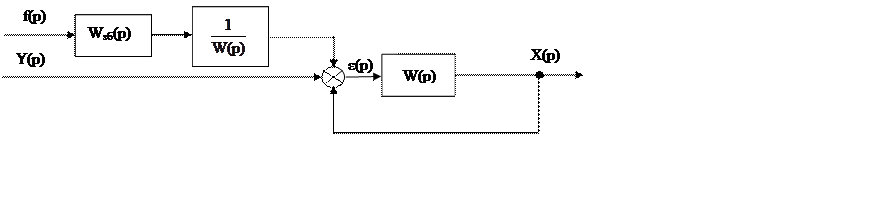Приймаючі до уваги, що вхідною величиною будемо вважати збурюючий вплив f(p) (Y(p)=0), а вихідною координата стану об’єкта керування Х(р), відповідна функція передачі для керованої величини Х(р)  по збуренню f(p)  матиме вигляд:

.

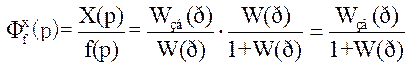Порівнюючи всі три різновиди функцій слід звернути увагу на тотожність їх знаменників. Це дуже важлива особливість, тому що знаменник являє собою ліву частину рівняння динаміки системи керування. Тож, прирівнявши вираз знаменника до нуля, отримаємо характеристичне рівняння, яке характеризує особисті властивості системи не пов’язані з характером та місцем прикладення зовнішніх впливів. Отже, яким би різновидом функції передачі не користуватися при вивченні особистих властивостей системи керування, наприклад таких як стійкість, отримаємо однаковий результат.  

Стійкість лінійних систем.

Під стійкістю системи автоматичного керування розуміють здатність системи повертатися до сталого режиму після зникнення зовнішніх сил, які вивели її з такого стану.

Для визначення стійкості системи розроблені певні вимоги до параметрів математичної моделі (коефіцієнтів рівнянь, коренів рівнянь динаміки) та деяких характеристик системи керування. Вказані вимоги, які повинні задовольнятися в стійких системах, мають назву критеріїв стійкості.

Кореневий критерій стійкості.

Припустимо, що диференціальне рівняння динаміки замкнутої системи в операторній формі запису має вигляд

A(p)x(t)=B(p)f(t),                   

де x(t) - керована координата; f(t) - зовнішній вплив; A(р) і B(р) поліноми оператора диференціювання р.

Коефіцієнти полінома A(р) залежать тільки від параметрів основного замкнутого контуру керування, а коефіцієнти полінома B(р) - ще й від місця прикладення зовнішнього впливу.

Рішення лінійного неоднорідного диференціального рівняння з постійними коефіцієнтами представляється у вигляді суми двох складових

x(t)=х_в (t)+x_з(t),                             

де х_в(t) - вільна складова руху в системі, обумовлена загальним рішенням   однорідного   диференціального   рівняння   A(p)x(t)=0;

х_з - змушена складова руху, що виникає внаслідок наявності зовнішнього впливу f(t) і обумовлена частковим рішенням неоднорідного диференціального рівняння, вона визначає усталений рух у системі.

У стійкій системі по закінченню перехідного процесу наступає сталий режим, обумовлений змушеною складовою х_з, отже, вільна складова руху х_в(t) повинна прагнути до нуля, тобто .  Рішення однорідного диференціального рівняння A(р) х_в(t)=0 відшукується у вигляді:

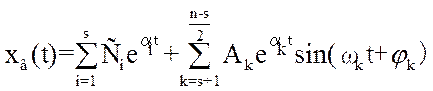
де n – ступень характеристичного рівняння М(р) = 0, загальна кількість коренів ;

 s –кількість дійсних коренів ;

р_і= -  дійсні корені характеристичного рівняння;

р_к= - комплексні корені;

 C_i, А_k,  - довільні постійні інтегрування.

Умова стійкості системи   буде виконуватися лише при   й , тобто коли дійсні корені та дійсні частини комплексних спряжених коренів характеристичного рівняння мають від’ємний знак.

Тобто ,необхідна умова стійкості полягає в тому, що в стійкій системі керування дійсні корені характеристичного рівняння та дійсні частини комплексних спряжених коренів мають бути від’ємними.

Якщо хоча б один корінь буде мати додатну дійсну частину, то відповідний йому член наведеної формули стане розбіжним й система виявиться нестійкою. Якщо відобразити розташування коренів на комплексній площині, то вони повинні розташуватися в лівій на півплощині відносно уявної осі. Уявну вісь, яка розмежовує області стійких та нестійких систем, називають межею стійкості.

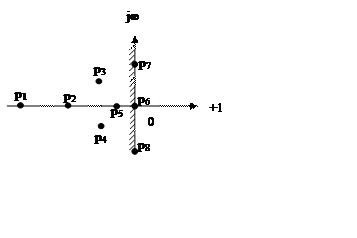 Система керування (при відсутності додатних дійсних частин коренів характеристичного рівняння) може знаходитися на межі стійкості у двох випадках:

1.  Якщо є хоча б один нульовий корінь (р₆), така система називається нейтральною. В такій системі може установити любе значення керованої величини.

2.  Якщо є хоча б одна пара чисто уявних кореня (р_7,8) (з нульовою дійсною частиною), то в такій системі встановлюються незатухаючі коливання з постійною амплітудою. В такому випадку межа стійкості називається коливальною межею стійкості.

Теореми стійкості Ляпунова.

Розглянуті вище вимоги до розподілу коренів  для забезпечення стійкості абсолютно застосовні до лінійних систем. Але ж реальні системи не є строго лінійними, лінійні характеристики ланок та їх лінійні диференціальні рівняння динаміки утворюються в результаті лінеаризації реальних рівнянь. При тому здійснюються певні спрощення (наприклад, відкидання членів вищого порядку малості), тому виникає питання, чи  не зроблять суттєвого впливу на стійкість систем ті фактори, якими ми нехтуємо? Відповідь на це питання дають теореми Ляпунова.

1-а теорема. Якщо характеристичне рівняння лінеаризованої системи має усі корені з від’ємними дійсними частинами, то реальна система також буде стійкою, тобто врахування малих членів розкладення Тейлора не можуть порушити стійкість системи.