Статические и астатические САР, страница 2

Величина, показывающая отношение ускорения регулируемой координаты к ошибке в установившемся режиме, называется добротностью САР по ускорению, которая численно равна коэффициенту усиления  разомкнутой САР:

.

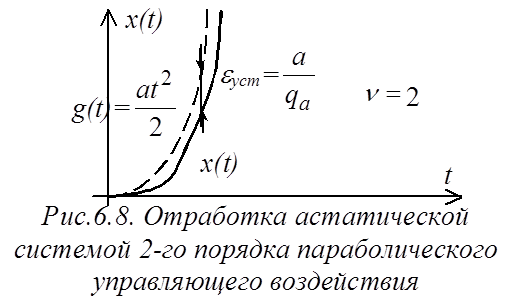
Термин добротность системы по скорости применяется к астатическим системам 1-го порядка, а термин добротность системы по ускорению – к астатическим системам второго порядка.

В обоих случаях, чем выше добротность q, тем меньше установившаяся ошибка , и тем точнее отработка системой управляющего воздействия.

Системы стабилизации

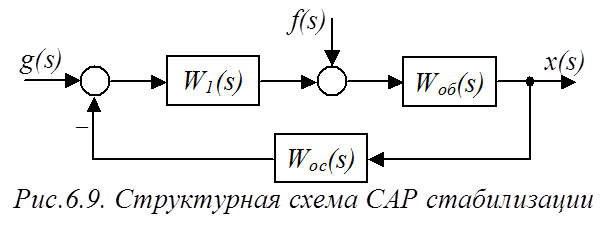
Выше уже отмечалось, что для систем стабилизации, помимо астатизма по управлению (как и в системах точного воспроизведения), важным является решение вопроса астатизма САР по возмущающему воздействию. Если возмущающее воздействие влияет на регулируемую координату в установившемся режиме, САР считается статической по возмущению, в противном случае – астатической.

Структурная схема системы стабилизации представлена на рис.6.9.

Для определения влияния возмущения необходимо сначала найти ПФ САР от возмущения к выходу. Приравниваем g(s)=0 и, считая цепь со звеньями  и  отрицательной ОС по отношению к возмущению, находим:

          ,

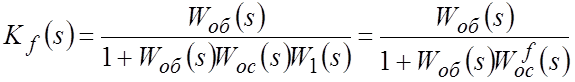где  – ПФ цепи ОС по отношению к возмущающему воздействию.

Представим ПФ в знаменателе последнего выражения в виде:

                ,

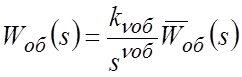
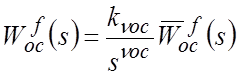где  – порядок астатизма ПФ ОУ;

       – порядок астатизма ПФ цепи ОС по отношению к возмущающему воздействию;

      ,  – соответствующие нормированные ПФ.

Тогда искомая ПФ

.

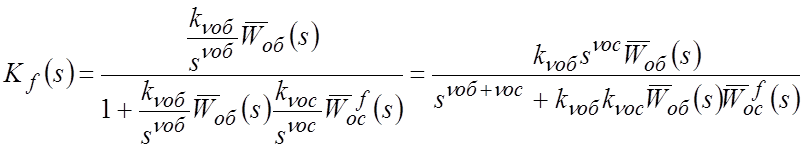Для исключения влияния возмущения на регулируемую координату (то есть, для обеспечения астатизма САР по возмущению) необходимо, чтобы . Из последнего выражения следует, что для этого необходимо, чтобы .

Астатизм САР по возмущающему воздействию определяется порядком астатизма цепи ОС по отношению к возмущению и не зависит от порядка астатизма ОУ. Другими словами, если чистые интеграторы отсутствуют в цепи ОС, то система будет статической, независимо от того, есть ли интеграторы в ОУ или нет.

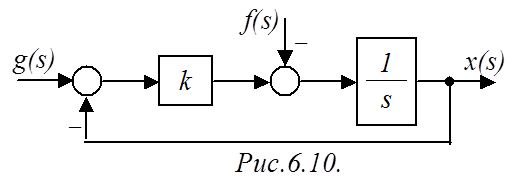
Пример 1. Определить, является ли система (рис.6.10) астатической по управляющему и возмущающему воздействиям?

Решение. Находим ПФ разомкнутой САР:

          .

Таким образом, , следовательно, по отношению к управляющему воздействию система астатическая 1-го порядка.

Находим ПФ цепи отрицательной ОС по отношению к возмущению:

          .

Таким образом, , следовательно, система является статической по отношению к возмущающему воздействию.

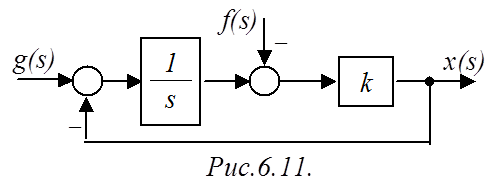
Пример 2. Определить, является ли система (рис.6.11) астатической по управляющему и возмущающему воздействиям?

Решение. Находим ПФ разомкнутой САР:

          .

Таким образом, , следовательно, по отношению к управляющему воздействию система астатическая 1-го порядка.

Находим ПФ цепи отрицательной ОС по отношению к возмущению:

          .

Таким образом, , следовательно, и по отношению к возмущающему воздействию система является астатической 1-го порядка.

Уравнения и передаточные функции системы

"силовой преобразователь – двигатель"

Принципиальная схема система "преобразователь – двигатель" представлена на рис.6.12а.

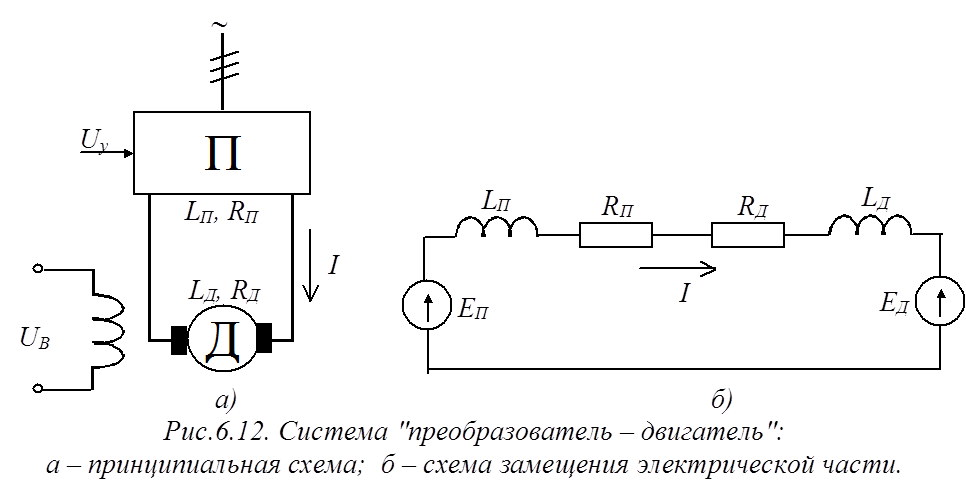
Тиристорный преобразователь П предназначен для выпрямления сетевого трехфазного напряжения, на его выходе имеем выпрямленное ЭДС преобразователя E_П, величина которого зависит от значения напряжения управления U_y. Электромагнитные свойства преобразователя характеризуются активным сопротивлением R_П и индуктивностью L_П.

ЭДС, наводимая в обмотке якоря двигателя E_Д направлена встречно с ЭДС преобразователя E_П и пропорциональна частоте вращения вала двигателя. Индуктивность и активное сопротивление цепи якоря двигателя Д

;          ,

где ,  – параметры цепи собственно якоря двигателя;  ,  – параметры обмотки добавочных полюсов;  ,  – параметры компенсационной обмотке.

Электрическая схема замещения электрической части системы "преобразователь – двигатель" представлена на рис.6.12б.

Обозначив

;  ,

дифференциальное уравнение электрического равновесия цепи якоря запишем в следующем виде:

                    .

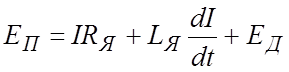Соответствующее уравнение в изображениях Лапласа:

.

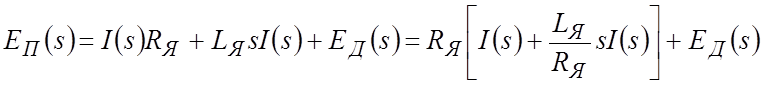Обозначим  – электромагнитная постоянная времени силовой цепи якоря двигателя, с. Тогда последнее уравнение запишется в виде:

          ,

откуда

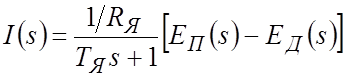                        .                        (1)

ЭДС двигателя пропорциональна частоте вращения вала:

          ,

или, переходя к изображениям Лапласа,

                        ,                        (2)

где  – конструктивная постоянная, пропорциональная номинальному магнитному потоку двигателя.

Наконец, уравнение механического равновесия

          ,

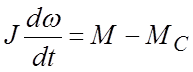где M – электромагнитный момент, развиваемый двигателем;  M_C – момент статического сопротивления (нагрузки);  J – суммарный момент инерции вала двигателя.

Уравнение электромагнитного момента имеет вид:

          ,

и формально статический момент может быть представлен в аналогичном виде:

                    ,

где  – ток статической нагрузки.

С учетом этого уравнение механического равновесия может быть представлено в виде:

          .

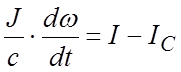Переходя к изображениям Лапласа:

          ,

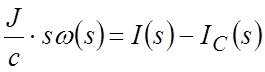после преобразований получим:

                        .

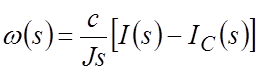Вводя понятие электромеханической постоянной времени 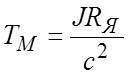, последнее уравнение представим в окончательном виде:

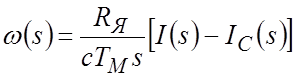              .                        (3)

Уравнениям (1) – (3) соответствует структурная схема, представленная на рис.6.13.

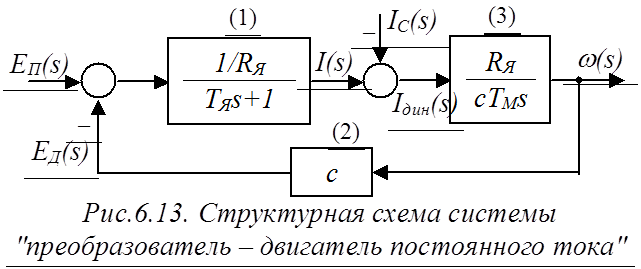
Анализируя структурную схему (рис.6.13), можно увидеть, что данная система астатическая по отношению к управляющему воздействию E_П(s) (поскольку присутствует чистый интегратор в блоке (3)), и в то же время статическая по отношению к возмущающему воздействию I_C(s) (в блоках (1) и (2) отсутствуют интеграторы). Таким образом, при изменении нагрузки I_C на валу двигателя будет изменяться и скорость w(s).

ПФ по управляющему воздействию:

.

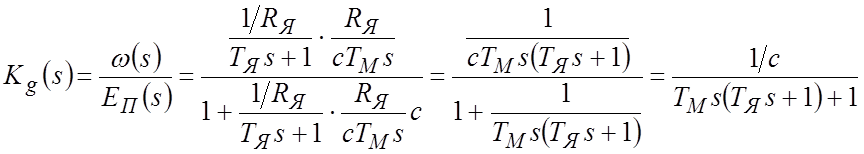В установившемся режиме

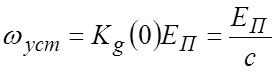                    ,                    и          .

ПФ по возмущающему воздействию:

.

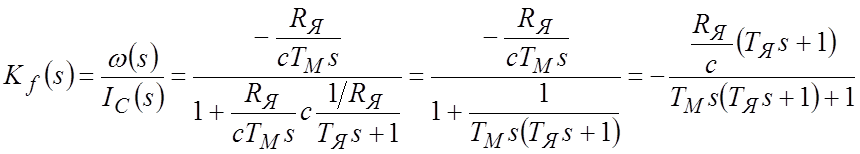Установившаяся ошибка:

          .

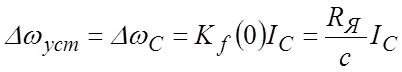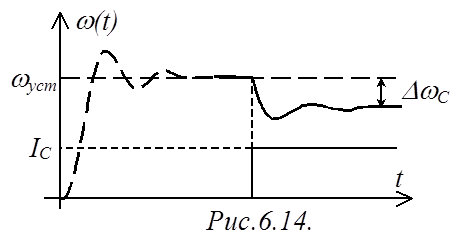Т.е., при подаче какого-то управляющего воздействия (рис.6.14) двигатель каким-то образом (показано пунктирной линией) разгонится до скорости . После скачкообразного приложения возмущающего воздействия (наброса нагрузки) будет иметь место ошибка регулирования, которая после затухания переходного процесса будет равна .

Сравнивая ПФ  и , видим, что знаменатели, т.е., характеристические полиномы двигателя, остаются одинаковыми вне зависимости от того, что является входом, и что – выходом.

Этот вывод можно распространить на любую замкнутую САР: характеристический полином  не зависит от того, на основании какой ПФ он записан.

Для определения характера переходного процесса при подаче управляющего воздействия рассмотрим детальней ПФ :

          .

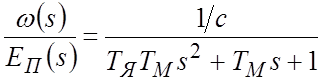Таким образом, если , будем иметь колебательное звено, если же , то данная ПФ является ПФ двух последовательно соединенных апериодических звеньев.

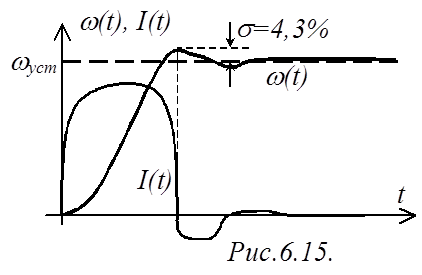Например, при  и  переходный процесс по току и скорости качественно будет иметь вид, показанный на рис.6.15. Отметим, что точки экстремума кривой w(t) совпадают по времени с нулевыми значениями I(t), поскольку ток, согласно (3), является производной от скорости.