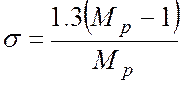. (5)
Можно также пользоваться эмпирическими формулами:
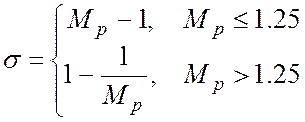(6)
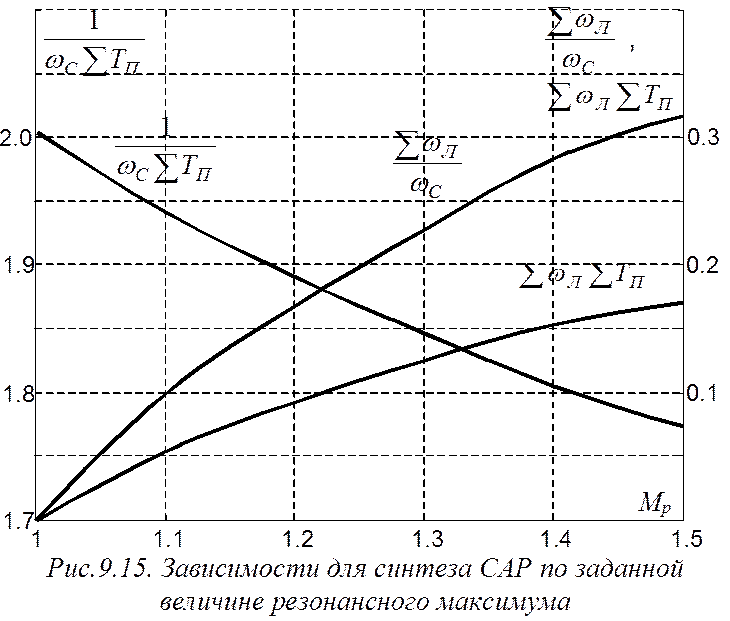
Рассмотрим алгоритмы решения задачи при разных формулировках:
Задача 1. Дано: wС, s и характер ЛАЧХ.
Определить: 
и 
.
Решение. Из формулы (5) определяем требуемое значение Мр:
.
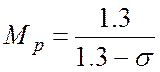По величине Мр из графиков рис.9.15
определяем числа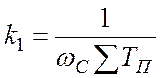 
и 
.
Далее определяем:
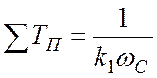и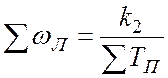 
.
Задача 2.
Дано: Мр, .
Определить: wС и .
Решение. По
величине Мр из графиков рис.9.15 определяем числа 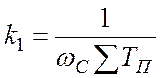и .
Далее определяем:
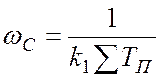и .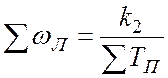
Задача 3.
Дано: , и
характер ЛАЧХ.
Определить: wС и Мр.
Решение. По
заданным и определяем
.
Затем по графику соответствующей зависимости рис.9.15 определяем Мр.
По найденному Мр из графиков
рис.9.15 определяем 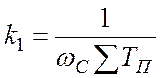и частоту среза .
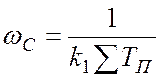В.А. Бесекерским установлены зависимости между Мр и требуемыми для его выполнения параметрами:
;
;
.
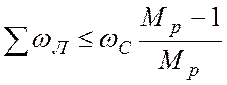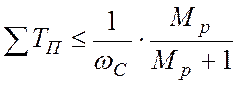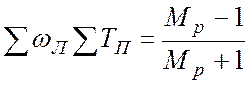Например, для Мр=1,5 имеем
.
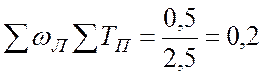Пример.
Задана система подчиненного регулирования скорости
двигателя постоянного тока (рис.9.16), в которой контур регулирования тока
(КРТ) синтезирован таким образом, что он представляет собой колебательное звено
с 
(
).
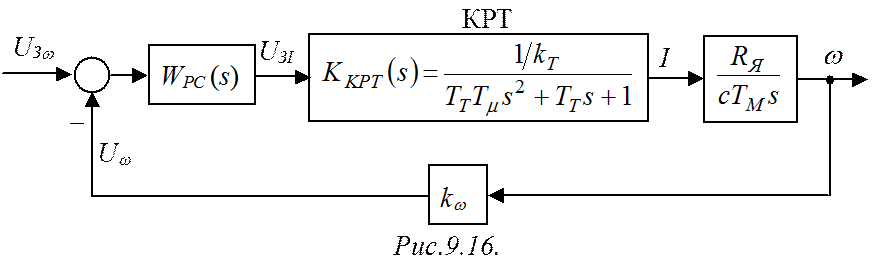
Тm – малая постоянная времени, не поддающаяся компенсации (обычно Тm =3…5 мс). kT – коэффициент ОС по току; kw – коэффициент ОС по скорости.
Считая, что инерционность КРТ компенсировать нецелесообразно, спроектировать астатическую систему первого порядка, обеспечивающую заданную точность в установившемся режиме:
n=1 c0=0 c1=Tm
Решение.
Поскольку задан коэффициент ошибки с1, необходимо, чтобы коэффициент усиления разомкнутой системы
. (*)
Передаточная функция разомкнутой САР:
,
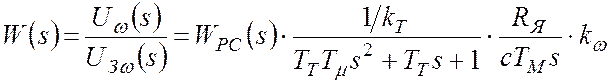или, после пренебрежения инерционностью КРТ:
.
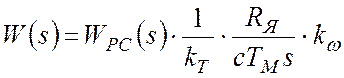Из последних формул видно, что
. (**)
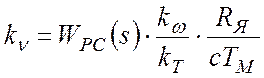Приравнивая (*) и (**), получаем, что
,
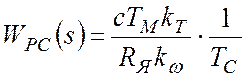где
– постоянная интегрирования
разомкнутого контура регулирования скорости (КРС).
В таком случае требуемая добротность САР по скорости будет обеспечена. При этом результирующая ПФ разомкнутого КРС:
.
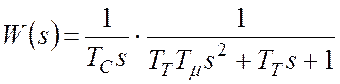Построим ЛАЧХ разомкнутого КРС при 
.
Характеристический полином представим в виде:
,
где
, 
;
.
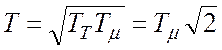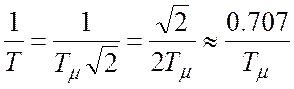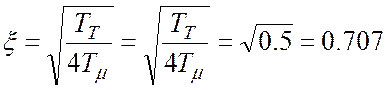ЛАЧХ разомкнутого КРС представлена на рис.9.17 (сплошная линия).
Будем решать задачу в такой постановке:
Синтезировать систему с требуемыми показателями по точности при условии, что заданное перерегулирование s=25%, а быстродействие будет максимальным. При решении задачи необходимо выполнить условие, что инерционность КРТ компенсироваться не будет, таким образом, желаемая ЛАЧХ в области высоких частот будет иметь такой же вид, как и ЛАЧХ неизменяемой части, т.е. наклон "–3".
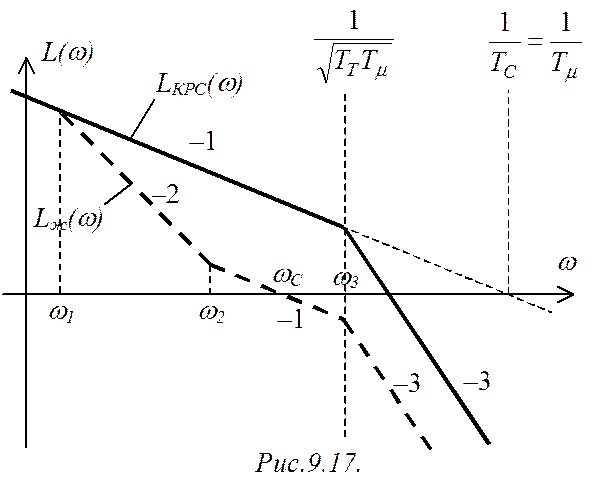
В соответствии с поставленной задачей перед синтезом
желаемой ЛАЧХ примем, что частота среза wС будет находиться левей частоты сопряжения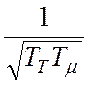 
, и будет сопрягаться с низко- и высокочастотными участками ЛАЧХ при
наклонах "–2" и "–3" соответственно (рис.9.17, прерывистая
линия). Значения wС и
частот сопряжения w1, w2 пока
неизвестны.
Тогда задача сводится к задаче 2.
Дано: Мр=1+s=1,25;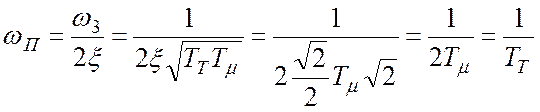 
;
.
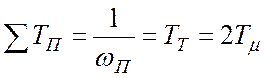Необходимо определить wС и .
По величине Мр из графика рис.9.15
определяем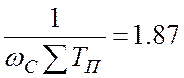 
, отсюда
.
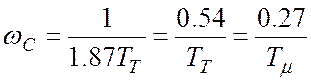Из вида желаемой ЛАЧХ следует, что
.
По значению Мр из графика рис.9.15
определяем 
, отсюда
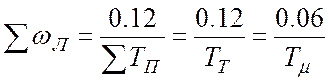
Например, при 
с:
с 
с-1 
с-1.
Таким образом, чтобы обеспечить желаемую ЛАЧХ, необходимо в регулятор скорости внести одно апериодическое звено и одно форсирующее звено 1-го порядка. Тогда ПФ регулятора скорости:
,
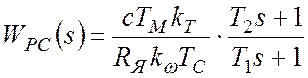а ПФ разомкнутого КРС:
.
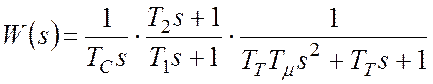Правило оперативного определения частоты среза wС:
1) необходимо в ПФ отбросить все те звенья, которые не влияют на частоту среза wС, т.е. звенья, частоты сопряжения которых находятся правее wС;
2) в ПФ апериодических, колебательных, форсирующих звеньев 1-го и 2-го порядков оставить только те значения, которые связаны со старшей степенью s;
3) в полученной таким образом ПФ s заменяют на wС, и приравнивают все выражение к единице.
Полученное в результате уравнение является основой для определения wС.
Например, для полученной результирующей ПФ разомкнутого КРС:
после п.1: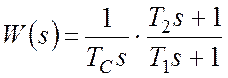 
после п.2: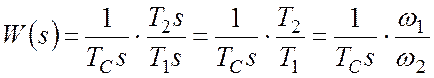 
после п.3: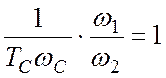 
Þ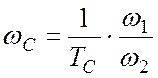 
Использование правила оперативного определения wС дает дополнительное условие для выбора частот сопряжения w1, w2:
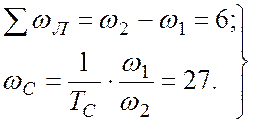Þ w1, w2
Вопросы синтеза параллельных корректирующих звеньев
Пусть в системе управления во внутренней ее части используется параллельное корректирующее звено (рис.9.18).
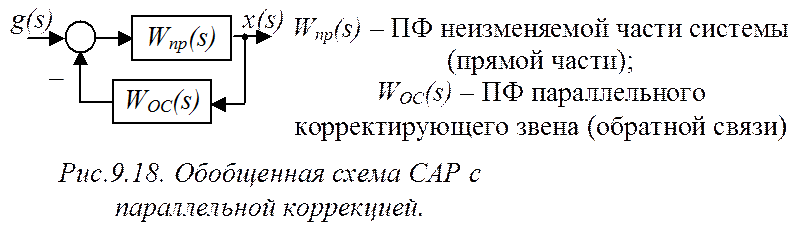
Нужно определить:
1. Каково влияние корректирующего звена?
2. Какова характеристика всего замкнутого контура?
Введем обозначения:
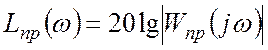– ЛАЧХ прямой части системы;
– ЛАЧХ цепи обратной связи;
Обратная ЛАЧХ цепи ОС
,
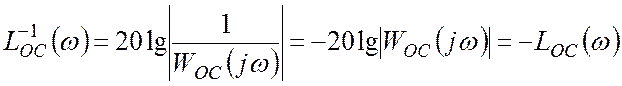т.е. равна зеркальному отображению ЛАЧХ цепи ОС относительно оси частот (рис.9.19а).
ЛАЧХ соединения, замкнутого отрицательной обратной связью:
,
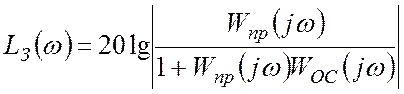состоит
из тех участков ЛАЧХ 
прямой части
и обратной ЛАЧХ 
цепи обратной связи,
которые имеют минимальную амплитуду (рис.9.19б).
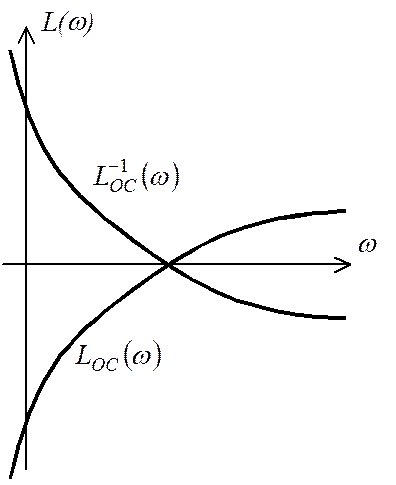
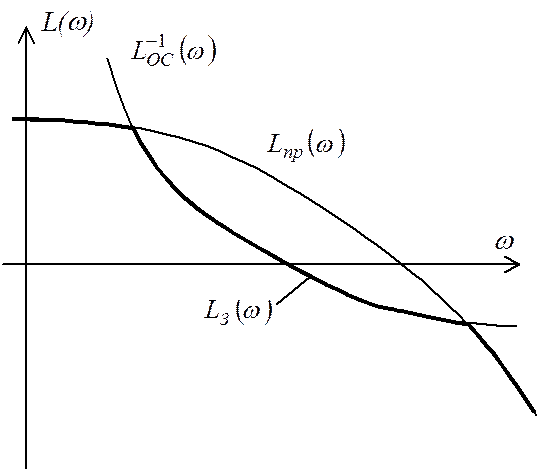
а) б)
Рис.9.19. Обратная ЛАЧХ цепи ОС (а) и ЛАЧХ соединения, охваченного отрицательной ОС.
Анализ ЛАЧХ 
позволяет прийти
к выводам:
1. Динамические свойства соединения, замкнутого отрицательной ОС, менее чувствительны к изменению параметров прямой части системы (поскольку параметры прямой части не влияют на среднечастотный участок ЛАЧХ).
2. Цепь ОС должна быть реализована на базе элементов с высокостабильными параметрами, так как обычные динамические свойства соединения в основном определяются параметрами цепи ОС.
Обычно при использовании параллельной коррекции после оценки полученных динамических свойств соединения следует проверить устойчивость замкнутой САР. При этом необходимо обеспечить запас устойчивости не менее 25…30°.
Проанализируем частный случай: при единичной отрицательной обратной связи (рис.9.20). В таком случае
; 
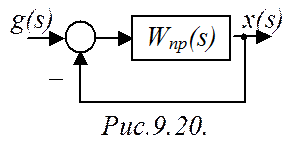
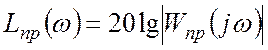
Т.е., обратная ЛАЧХ цепи ОС в данном случае совпадает
с осью частот. Поэтому и ЛАЧХ соединения не
может заходить в область положительных значений (рис.9.21).
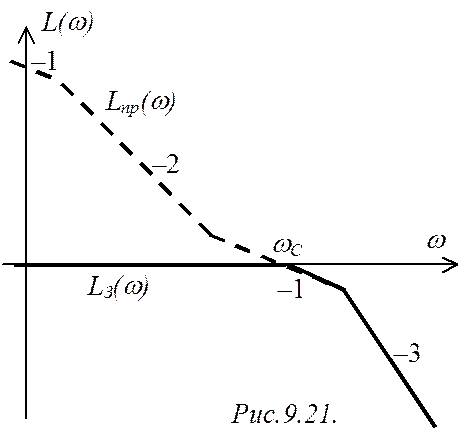
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.