Функция ищет и вещественные и комплексные корни, но начальное приближение надо задать как комплексное число.
Для нахождения корней полинома polyroots(v), не надо начальное приближение корней и сразу все корни как вещественные так и комплексные. v - вектор кэфов полинома длины n+1, где n - степень полинома. На выходе вектор длины n из корней полинома.
Можно решать системы ур и неравенства. Max число ур и нерав - 50. Наиболее распростр блочный метод:
- задаем начальное приближение для всех действий
- задаем ключевое слово Given, указывает, что далее следует система ур
- ввод ур или нерав (исп логическое =)
- ввод любого выражния, которое включает функцию Find (возвращ точное приближенное значение)
- Find может возвращ результ:
- Find(var1,var2,..)
- var:=Find(var1,var2,..) - вектор
- определить другую функцию с пом Find F(a,b,c...):=Find(x,y,z,...) Это позволяет найти решение при различных начальных приближениях.
Внутри решающего блока недопустимы: неравенства, дискретные выражения, исп дискретные переменные, неравенства вида a<b<c, вложенные блоки.
Приближенное решение системы можно получить с пом функции Minner.
В MathCad можно решать линейные системы матричным методом (функция lsolve решает обратную матрицу).
В MatLAB полиномиальные ур-я решаются функцией roots(a), где a - вектор коэфов перед неизвестными полинома размерностью n+1. Результат - вектор корней полинома размерностью u. Решить 3x3+x2-10x+8 = 0
u=[3 1 -10 8] roots(u)
Для решения нелинейного ур-я f(x)=0 исп fzero(F,x0), где F - имя функции F(x) исх ур-я, x0 - начальное приближение корня. Пример: решить cos(x)-0.1x=0
fzero('cos(x)-0.1x',1)
Если задана сист лин ур вида Ax=B, то реш вида x=A/B или x=inv(A)*B
Реш сист нелин ур вып с пом Fsolve(f,v), F - имя функции, содерж вектор левых частей сист ур, v - вектор нач условий. Решить sinx+2y=2 sin(y-2)-x=-1.
Последовательность решения:
- создаем M-файл левых частей: function F=fu(x)
f=[sin(x(1))+2*x(2)-2; sin(x(2)-2)-x(1)+1];
- записать файл на диск с имененм Fu.m
- создать m-файл решения сист ур a=Fsolve(@Fu,[1,1])
- после запуска на выполнение в переменной а будут корни
11.Методы численного интегрирования и их реализация в Mathcad и Matlab.
12. Методы построения статических моделей
Статическая модель тех объекта, в которой не учитывается изменение параметров во времени. Она описывается алгебраическим уравнением или системой линейных или нелин уравн, в завис от св-в объекта. Статич модель может описываться функцией
y=F(x) - в явном виде
F(x,y)=0 - в неявном виде
В явном виде:
y1=F1(x1,x2,...,xn)
.......
ys=Fs(x1,x2,...,xn)
В линейной модели параметры тех объекта связны линейными соотношениями. При изменении внешнего или внутреннего параметра, линейная модель предсказывает линейное изменение зависящего от него выходного параметра. Для линейной статич модели справедлив принцип суперпозиции: реакция суммы воздействий есть сумма реакций на каждое воздействие y(x1+x2)=y(x1)+y(x2)
Нелинейная модель определяется нелинейной функцией: y=f(x1,..,x1,c1,..,cn), где с - некоторые неизвестные или неточно известные const. Нет принципа суперпозиции.
Мат модель системы статическая, если значение выхода Y(t) зависит от входа X(t) только в тот же момент времени t. Y(t)=F(x(t)), где А - некоторый оператор.
Статич модель строится, когда тех объект соотв ряду условий:
- система устойчива, т.е. переходные процессы после скачкообразного изменения входов затухают
- выходы меняются медленно и изменяются редко
Для мех систем можно создавать 2 вида статич моделей в завис от состояния сист: модель для состояния покоя и для сост равномерного движения.
13. Построение моделей по результатам эксперимента.
Для этого применяется аппроксимация. Направления применения:
– Обработка результатов эксперименты по компьютерной модели
– Обработка результатов натурного эксперимента, синтез модели.
– Создание робастных моделей элементов при моделировании систем.
Компьютерный эксперимент - модель, построенная в численном виде в кач вых параметров, имеет дискретные функции, для получения новых значений которых нужно проводить новый эксперимент по модели. Чтобы не проводить новые эксперименты по модели надо заменить табличную результирующую функцию аналитической функцией, полученной путем аппроксимации.
Второе направление – позволяет применить методы аппроксимации к дискретным данным, полученными, как правило, в виде файлов после проведения натурных экспериментов с применением специальных датчиков
Третье направление – замена точной модели элемента в системе робастной модели (грубой, приближенной) при синтезе моделей сложных технических систем. Подразумевается, что робастные модели должны выдерживать ошибки, которые теми или иными способами могут попадать в исходные данные.
Пример
1-го направления: в электрич
схеме с переменным сопротивлением надо получить аналитическую функцию и
значения max напряжения на конденсаторе в завис от емкости кондера
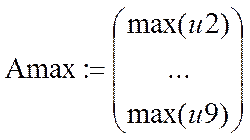
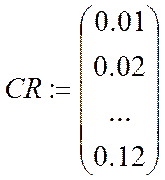– вектор
значений изменяемого внутреннего параметра
– экстремальное значение выходного сигнала.
Выполняем аппроксимацию
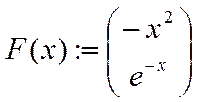H:=linfit(CR,Amax,F)
g(m):=F(m)·k m:=0,0.01..0.13
Пример 2-го направления: надо получить аппроксимирующую зависимость изменения значений ЭДС индукции от времени. Результаты эксперимента заданы в виде данных, которые надо предварительно сгладить. Функция loess позволяет аппроксимировать данные локальными полиномами 2-го порядка, исследуя данные в окрестности точки, представляющей интерес. Отличие от функции regress что regress приближает все точки данных используя 1 полином, а loess исп множество полиномов. Loess(VX, VY, span), span – величина, задающая длину отрезка, чем<, тем лучше значение данных.
После получения нового вектора ищем min и max элементы, проводим аапрокстимацию.
14. Аппроксимация и интерполяция. Математические определения
Аппроксимация - замена исходной функции F(x) функцией φ(x) так, чтобы отличие F(x) от φ(x) в заданной области было min. φ(x) - аппроксимирующая. Если исходная F(x) задана таблично (дискретно), то аппроксимирующая наз дискретной. Если F(x) задана на отрезке, то аппроксимирующая - непрерывная или интегральная.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.