Лекция 3
(4 часа)
ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ
Алгебра передаточных функций
1. Последовательно соединение звеньев.
Эквивалентная ПФ ![]() последовательно
соединенных звеньев с ПФ
последовательно
соединенных звеньев с ПФ ![]() и
и ![]() равна произведению этих ПФ
(рис.3.1):
равна произведению этих ПФ
(рис.3.1):
![]() .
.

Доказательство. Для структурной схемы (рис.3.1а) справедливы уравнения в изображениях Лапласа:
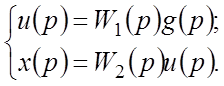
Подставив первое уравнение во второе, получим:
![]() ,
,
причем этому уравнению соответствует структурная схема рис.3.1б.
2. Параллельное соединение звеньев.
Эквивалентная ПФ ![]() параллельно
соединенных звеньев с ПФ
параллельно
соединенных звеньев с ПФ ![]() и
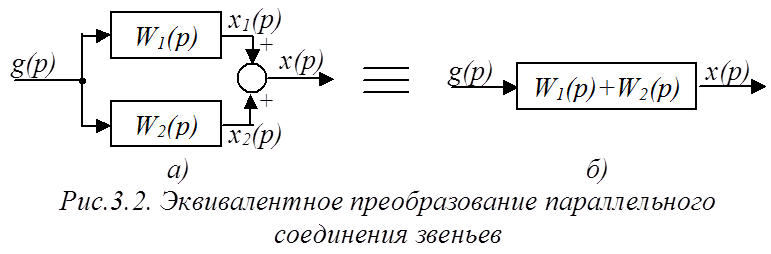
и ![]() равна сумме этих ПФ (рис.3.2):
равна сумме этих ПФ (рис.3.2):
![]() .
.
Доказательство. Для структурной схемы (рис.3.2а) справедливы уравнения в изображениях Лапласа:
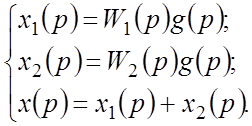
Подставив первые два уравнения в третье, получим:
![]() ,
,
причем этому уравнению соответствует структурная схема рис.3.2б.
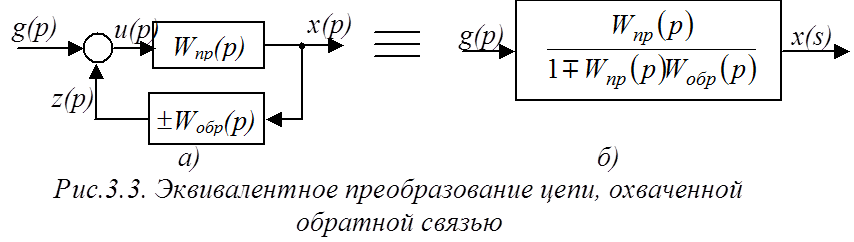
3. Передаточная функция цепи, охваченной обратной связью.
Эквивалентная ПФ ![]() цепи
(прямой части САР) с ПФ
цепи
(прямой части САР) с ПФ ![]() , охваченной обратной
связью с ПФ
, охваченной обратной
связью с ПФ ![]() (положительной или отрицательной)
равна (рис.3.3):
(положительной или отрицательной)
равна (рис.3.3):
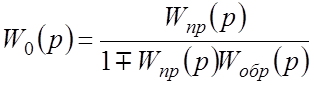 .
.
Доказательство. Система уравнений для структурной схемы рис.3.3а имеет вид:
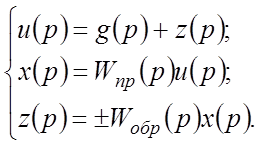
Из второго уравнения выразим:
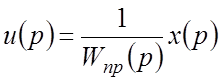 .
.
Теперь это выражение и третье уравнение системы подставим в первое уравнение:
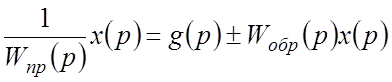 .
.
Последовательно преобразуем это уравнение:
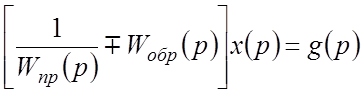 ;
;
![]() ;
;
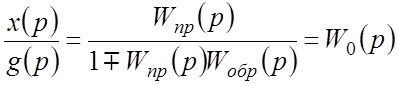 .
.
Последнее уравнение соответствует структурной схеме рис.3.3б.
4. Перенос точки съёма воздействия.
а) перенос вперед (с входа звена на выход) (рис.3.4).
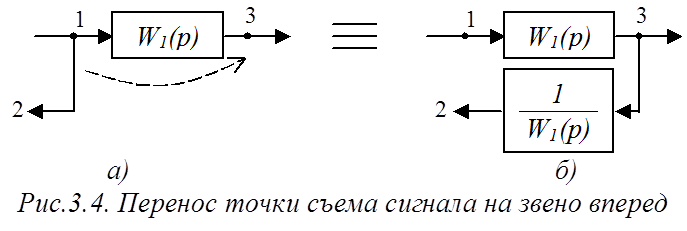 Перенос точки разветвления должен быть эквивалентным.
Переход из точки 1 в точку 2 (рис.3.4а), очевидно, происходит с ПФ (коэффициентом),
равной 1. Если просто перенести точку съема из 1 в 3, то получится, что теперь
в точку 2 сигнал будет переходить с коэффициентом W1(p). Для
компенсации этого необходимо поставить звено с обратной ПФ (рис.3.4б).
Перенос точки разветвления должен быть эквивалентным.
Переход из точки 1 в точку 2 (рис.3.4а), очевидно, происходит с ПФ (коэффициентом),
равной 1. Если просто перенести точку съема из 1 в 3, то получится, что теперь
в точку 2 сигнал будет переходить с коэффициентом W1(p). Для
компенсации этого необходимо поставить звено с обратной ПФ (рис.3.4б).
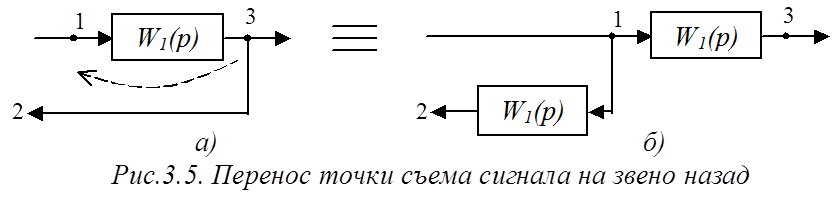
б) перенос назад (с выхода звена на вход) (рис.3.5).
Эквивалентный перенос из точки 3 в точку 1 (рис.3.5а) выполняется из тех же соображений, что и перенос вперед. Эквивалентная структурная схема представлена на рис.3.5б.
5. Перенос точки приложения воздействия (перенос сумматора).
а) перенос вперед (с входа звена на выход) (рис.3.6).
Этот перенос также основан на принципе эквивалентности. В схеме рис.3.6а выходной сигнал x формируется в результате передачи суммы сигналов g1+g2 с ПФ W1(p). Если просто перенести сумматор через звено, окажется, что воздействие g2 будет передаваться с коэффициентом единица. Для коррекции этого в канале передачи воздействия g2 следует установить звено с ПФ W1(p) (рис.3.6б).
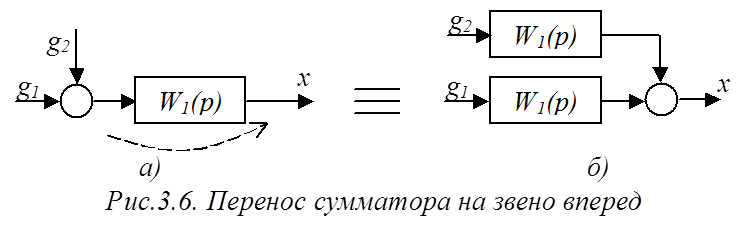
Правильность такого преобразования подтверждается тем, что математические описания схем рис. 3.6а и 3.6б совершенно идентичны.
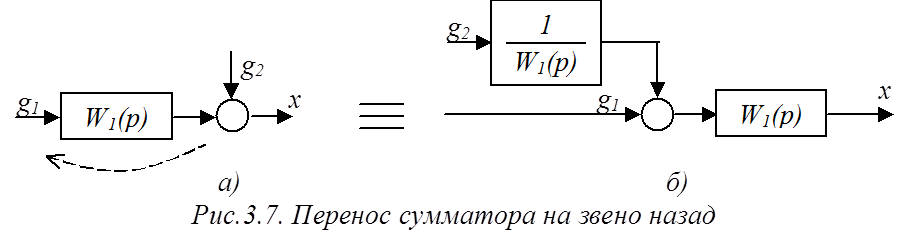
б) перенос назад (с выхода звена на вход) (рис.3.7).
Этот перенос производится, исходя из аналогичных рассуждений.
6. Преобразование структурных схем на основе принципа линейности.
Повторим формулировку принципа линейности: Реакция линейной САР на сумму воздействий равна сумме реакций САР на каждое воздействие в отдельности.
Сущность применения этого принципа будет раскрыта позднее.
Пример. Найти ПФ САР, структурная схема которой изображена на рис.3.8, используя преобразование структурной схемы.
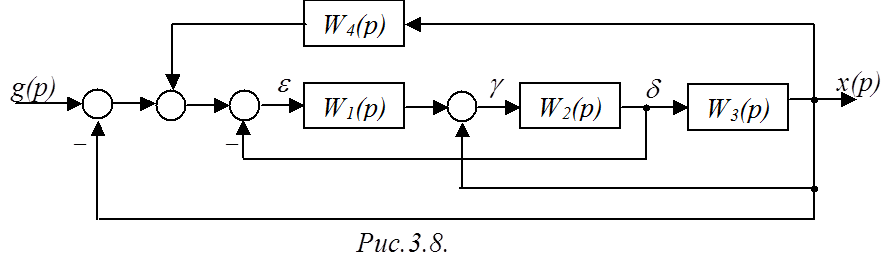
Решение.
Переносим точку съема сигнала d на звено вперед, используя правило 4а (рис.3.9).
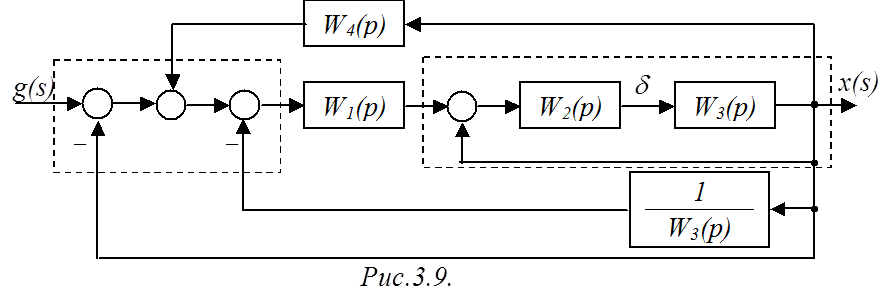
Для выделенной за блоком W1(p) части схемы находим эквивалентную ПФ, используя правило 3 для цепи, охваченной положительной обратной связью:
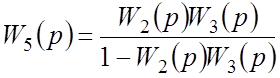 .
.
На три сумматора в начальной части схемы параллельно приходит один и тот же сигнал, но с разными ПФ. Используя правило 2, находим общую ПФ ветви отрицательной обратной связи:
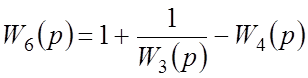 .
.
Теперь структурную схему можно представить в виде (рис.3.10).
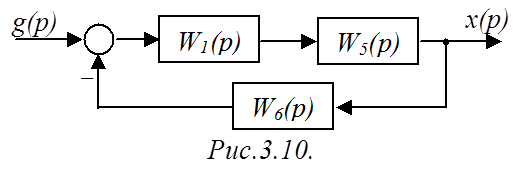
По схеме рис.3.10 определяем результирующую ПФ, используя правило 3:
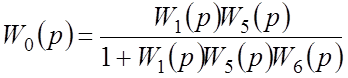 .
.
Передаточные функции разомкнутых и замкнутых САР
Выше отмечалось, что современные регулируемые ЭП, обладающие высококачественными динамическими и статическими характеристиками, как частный случай высококачественных САР, строятся с использованием отрицательной обратной связи (ОС), то есть, работают по замкнутому циклу. Рассмотрим обобщенную схему такой САР, состоящую из прямой ветви, охваченной отрицательной ОС (рис.3.11).
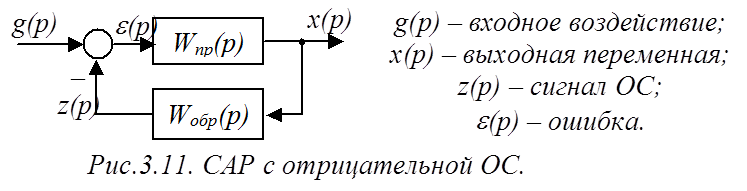
Передаточная функция замкнутой САР определяется по правилу 3 преобразования структурных схем:
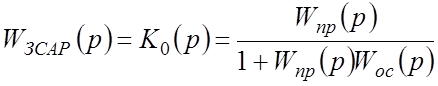 ,
,
где
![]() – ПФ прямой части САР, связывающая
вход с интересующим нас выходом;
– ПФ прямой части САР, связывающая
вход с интересующим нас выходом; ![]() – ПФ цепи ОС.
– ПФ цепи ОС.
При обозначении ПФ замкнутых систем вместо символа W используется символ K.
Смысл ПФ замкнутой САР в том, что она показывает, как входной сигнал g(p) преобразуется в выходной x(p):
![]() .
.
Передаточная функция разомкнутой САР получается после размыкании замкнутой САР (рис.3.11) в произвольном месте, и рассмотрения образовавшегося разомкнутого контура как последовательного соединения звеньев, не учитывая знак сумматора. Таким образом, используя правило 1, ПФ разомкнутой САР запишем в виде:
![]() .
.
Смысл ПФ разомкнутой САР в том, что она показывает, как сигнал ошибки e(p) преобразуется в сигнал обратной связи z(p).
Отметим такие важные моменты:
1. ПФ разомкнутой САР ![]() не
зависит от места размыкания САР.
не
зависит от места размыкания САР.
2. Неправильно считать, что ПФ разомкнутой САР равна ПФ САР, полученной после отбрасывания цепи ОС.
3. ПФ разомкнутой САР совпадает с ПФ прямой части САР
только в одном случае, когда ![]() .
.
Связь между ПФ разомкнутой и замкнутой САР выражается следующей формулой:
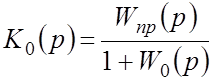 ,
,
то есть, ПФ цепи, замкнутой отрицательной ОС, равна ПФ прямой части, разделенной на ПФ разомкнутой САР, увеличенную на единицу.
В редких случаях, когда ОС положительная, в знаменателе ПФ замкнутой САР символ "+" меняется на "–".
Понятие о графе САР. Связь графа со структурной схемой
Граф прохождения сигнала, или сигнальный граф разработан Мейсоном (Mason) в 1953 для наглядного представления и описания связи между переменными устройств, описываемых системой линейных алгебраических уравнений. Так как стационарная линейная САР в изображениях Лапласа также описывается системой линейных алгебраических уравнений, сигнальный граф стал использоваться и для описания САР, и называться графом САР.
Граф САР состоит из дуг и вершин, и представляет собой упрощенный, менее громоздкий вариант изображения структурной схемы. Графы САР более наглядны, и широко используются при представлении структур САР.
Дуга на схеме изображается отрезком кривой со стрелкой, указывающей направление распространения сигнала. Дуга соответствует звену и характеризуется оператором (ПФ). Дуга начинается и заканчивается в вершине.
Вершина на схеме изображается точкой или кругом, и представляет переменную. Если из вершины выходят несколько дуг, то входная переменная этих дуг одна и та же. Если же в вершину приходят несколько дуг, то переменная, соответствующая вершине, равна сумме выходных переменных дуг.
Для построения графа САР по ее структурной схеме выполняется следующее:
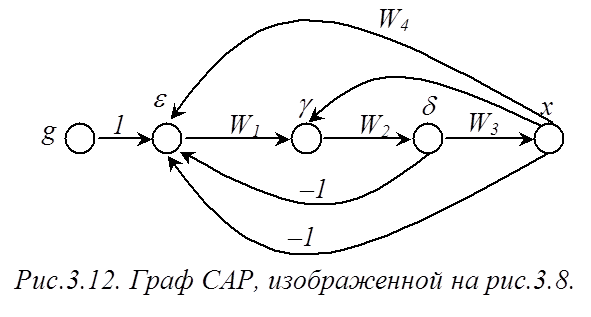
Из изложенного ясно соответствие между структурной схемой и графом. В качестве примера на рис.3.12 представлен граф САР, структурная схема которой изображена на рис.3.8.
Правило Мейсона (Мезона)
Это правило позволяет определить ПФ сколь угодно сложной замкнутой САР, не прибегая к преобразованию ее структурной схемы. Для его формулирования введем следующие определения:
Путем между двумя координатами (простым или прямым путем) называется последовательность линий и звеньев между этими двумя координатами такая, что каждое звено и каждая промежуточная координата встречаются только один раз. Передаточная функция пути равна произведению ПФ звеньев, встречающихся на этом пути.
Контур – это замкнутый путь. Другими словами – это такой путь, когда входная и выходная координаты совпадают. Передаточная функция замкнутого контура равна произведению ПФ звеньев, входящих в него, с учетом знаков сумматоров (если сигнал поступает на вход "+", ПФ сумматора равна единице, если на "–" – то –1.
Пример. Рассмотрим структурную схему рис.3.13а.
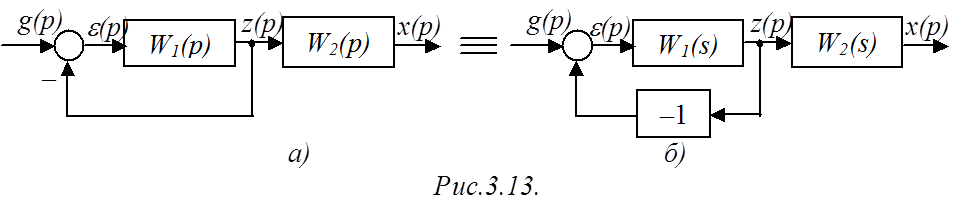
В схеме
присутствует один прямой путь – ![]() – с ПФ
– с ПФ ![]() , и также один замкнутый контур –
, и также один замкнутый контур – ![]() – с ПФ
– с ПФ ![]() ,
где наличие знака "минус" понятно из эквивалентной схемы рис.3.13б.
,
где наличие знака "минус" понятно из эквивалентной схемы рис.3.13б.
Правило Мейсона гласит:
Передаточная функция САР относительно каких либо входа g и выхода x может быть определена по формуле:
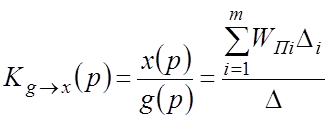 ,
,
где
![]() – ПФ i-го прямого
пути; m – число прямых путей;
– ПФ i-го прямого
пути; m – число прямых путей;
![]() – главный определитель (определитель
графа САР), вычисляемый по правилу:
– главный определитель (определитель
графа САР), вычисляемый по правилу:
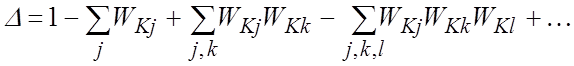 ,
,
где
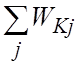 – сумма ПФ всех замкнутых контуров
структурной схемы;
– сумма ПФ всех замкнутых контуров
структурной схемы;
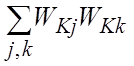 –
сумма произведений всех пар контуров, которые не касаются друг друга (не имеют
общих звеньев);
–
сумма произведений всех пар контуров, которые не касаются друг друга (не имеют
общих звеньев);
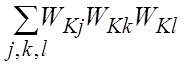 –
сумма произведений всех троек контуров, которые не касаются друг друга;
–
сумма произведений всех троек контуров, которые не касаются друг друга;
![]() – определитель i-го
прямого пути (определитель подграфа i-го
прямого пути), который вычисляется по
тому же правилу, что и главных определитель
– определитель i-го
прямого пути (определитель подграфа i-го
прямого пути), который вычисляется по
тому же правилу, что и главных определитель ![]() ,
но с учетом того, что учитываемые контуры, пары контуров, тройки контуров и
т.д. не должны касаться i-го прямого пути. В частном случае, когда все контуры
касаются i-го пути,
,
но с учетом того, что учитываемые контуры, пары контуров, тройки контуров и
т.д. не должны касаться i-го прямого пути. В частном случае, когда все контуры
касаются i-го пути, ![]() .
.
Примеры. Найти ПФ от входа к выходу по правилу Мейсона.
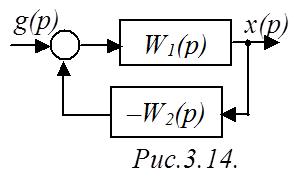
Схема рис.3.14 содержит один прямой путь с ПФ WП=W1, и один контур с ПФ WK=–W1W2. Тогда ![]() , а
, а ![]() .
Следовательно, искомая ПФ равна
.
Следовательно, искомая ПФ равна
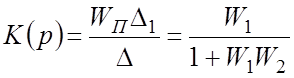 .
.
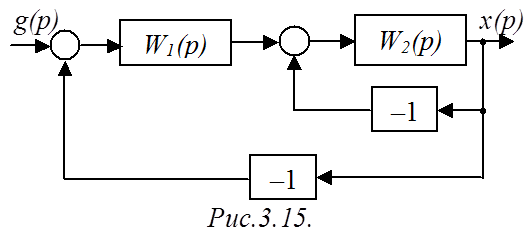 Схема рис.3.15 содержит один прямой путь с ПФ WП=W1W2, и
два контура с ПФ WK1=–W1W2
(внешний) и WK2=–W2 (внутренний), которые
соприкасаются между собой (через звено W2), а также касаются прямого пути. Тогда
Схема рис.3.15 содержит один прямой путь с ПФ WП=W1W2, и
два контура с ПФ WK1=–W1W2
(внешний) и WK2=–W2 (внутренний), которые
соприкасаются между собой (через звено W2), а также касаются прямого пути. Тогда ![]() , а
, а ![]() .
Искомая ПФ равна:
.
Искомая ПФ равна:
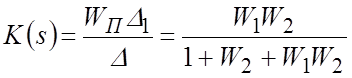 .
.
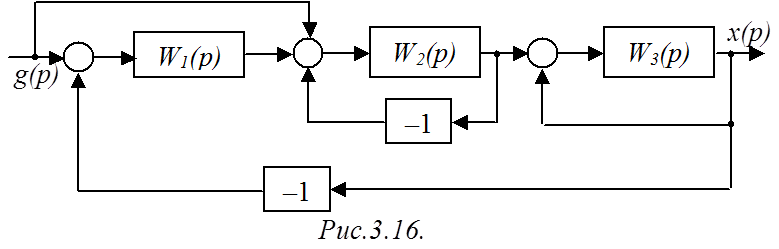
Схема рис.3.16 содержит два прямых пути с ПФ WП1=W1W2W3 и WП2=W2W3, и три контура с ПФ WK1=–W2, WK2=W3 (внутренние) и WK3=–W1W2W3 (внешний). Все контуры касаются обоих прямых путей. Два контура – WK1 и WK2 – не касаются друг друга.
Тогда ![]() ,
, ![]() , а
, а ![]() .
Искомая ПФ равна:
.
Искомая ПФ равна:
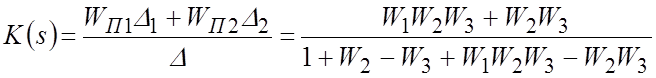 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.