1.1. Заданная передаточная функция звена с заданными значениями параметров.
Колебательное звено
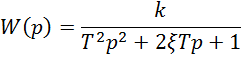
Значения параметров
|
k |
10 |
|
T |
1 |
|
ξ |
0.3 |
1.2. Изложение заданного метода моделирования применительно в заданному звену.
Способ разложения на уравнения первого порядка.
Данный способ заключается в записи дробно-рациональной передаточной функции в виде дифференциального уравнения, потом представление его в виде совокупности линейных дифференциальных уравнений первой степени. После чего требуется определить коэффициенты составленных уравнений первого порядка и подставить их(коэффициенты) в эти уравнения.
1.3. Соображения по выбору и выбранные значения шага интегрирования Δt и величины интервала интегрирования L.
Шаг интегрирования рассчитываем по формуле:
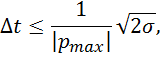
![]()
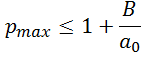
![]()
В моём
случае ![]() ,
,
![]() тогда:
тогда:
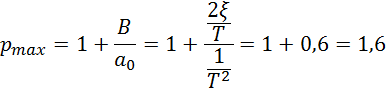
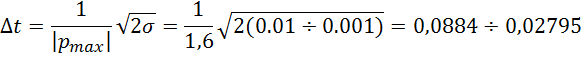
Интервал интегрирования для звена второго порядка определяем по формуле:
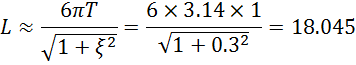
1.4. Листинг фрагмента программы, относящегося к моделированию заданной передаточной функции.
//ОБЛАСТЬ КОНСТАНТ И ПЕРЕМЕННЫХ
//(параметры объекта, шаг интегрирования, интервал моделирования и т.д.)
const
Lin = 20.0; //интервал моделирования
dt = 0.009; //шаг интегрирования
ksi=0.3;
k=10;
T=1.0;
g=1.0;
var
sumdt,
k11,k12,k21,k22,k31,k32,k41,k42, //текущее время моделирования
y,y1,y2,ypr, //переходная функция
w //весовая функция
: Real;
begin
////////////////////////////////////////////
//НАЧАЛЬНЫЕ УСЛОВИЯ
sumdt:=0;
y:=0;ypr:=0; y1:=0;y2:=0;
////////////////////////////////////////////
//НАЧАЛО МОДЕЛИРОВАНИЯ
REPEAT
////////////////////////////////////////////
//УРАВНЕНИЯ ПЕРЕХОДНОГО ПРОЦЕССА
k11:=y2*dt;
k12:=(-(2*ksi/T)*y2-(1/(T*T))*y1+(k/(T*T))*g)*dt;
k21:=(y2+(k12/2))*dt;
k22:=(-(2*ksi/T)*(y2+k12/2)-(1/(T*T))*(y1+k11/2)+(k/(T*T))*g)*dt;
k31:=(y2+(k22/2))*dt;
k32:=(-(2*ksi/T)*(y2+k22/2)-(1/(T*T))*(y1+k21/2)+(k/(T*T))*g)*dt;
k41:=(y2+k32)*dt;
k42:=(-(2*ksi/T)*(y2+k32)-(1/(T*T))*(y1+k31)+(k/(T*T))*g)*dt;
y1:=y1+(k11+2*k21+2*k31+k41)/6;
y2:=y2+(k12+2*k22+2*k32+k42)/6;
y:=y1;
w:=(y-ypr)/dt;
ypr:=y;
1.5. Полученные путём моделирования графики переходной и весовой функции.
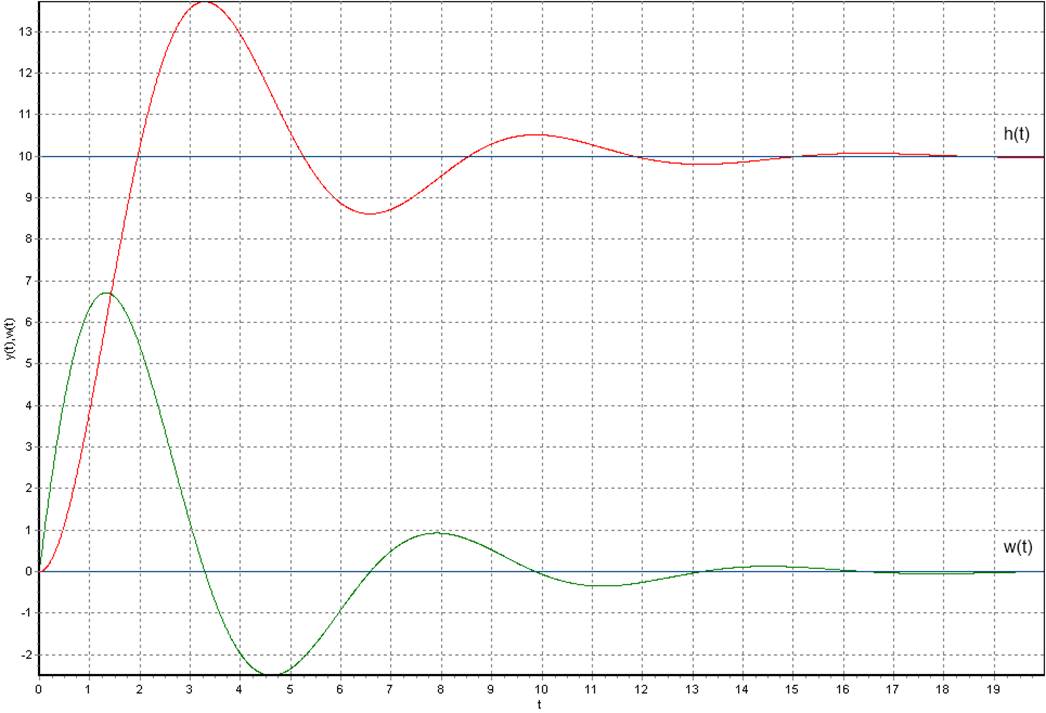
1.6. Описание процесса определения параметров заданной передаточной функции.
Для определения
параметров воспользуемся методикой изложенной в учебнике Бессекерского В.А.
"Теория систем автоматического регулирования" для колебательного
звена: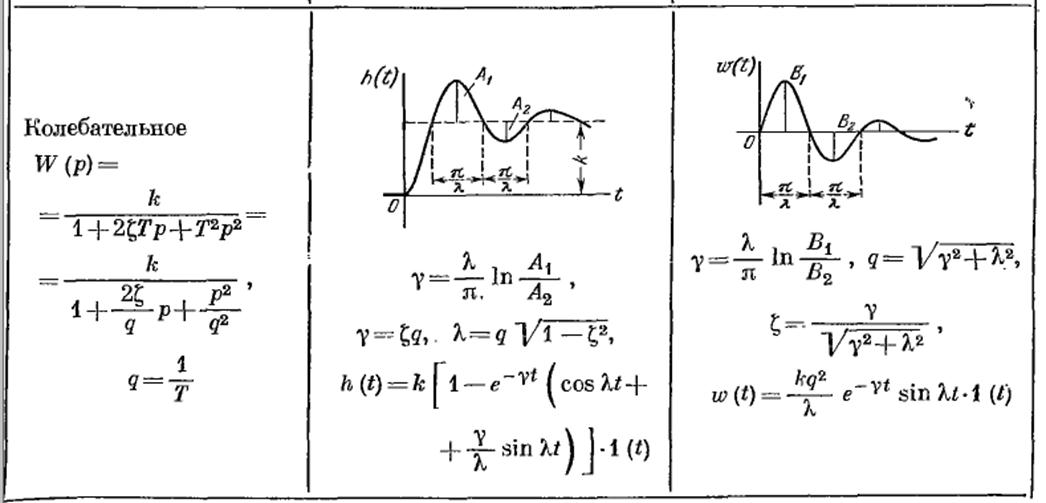
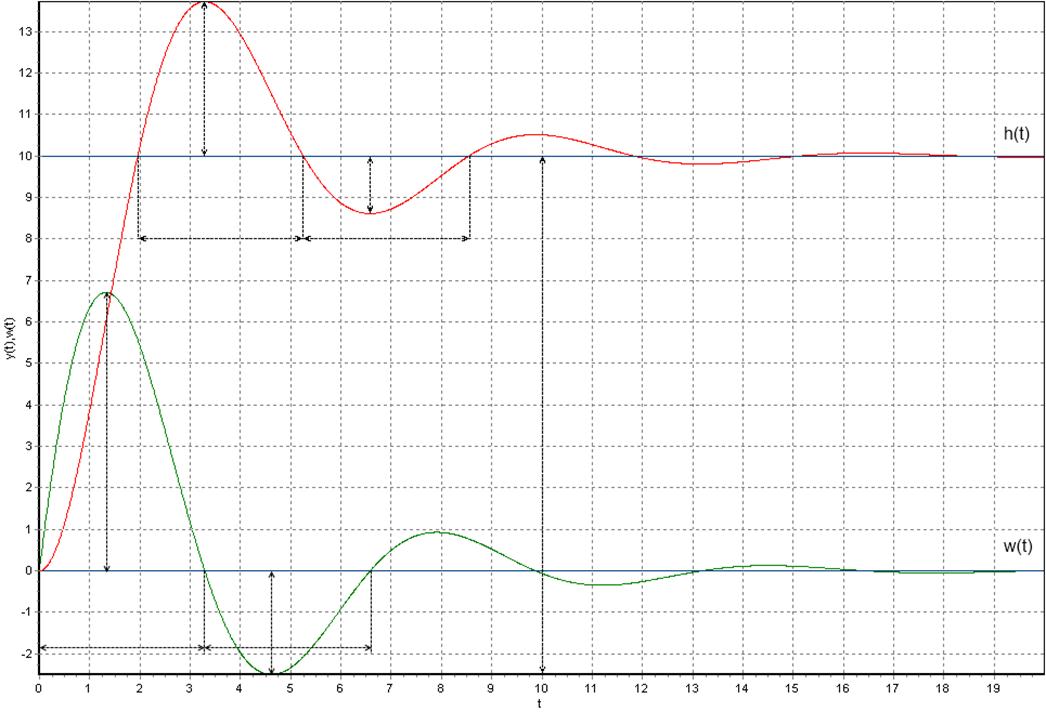 Найдём
нужные для расчёта данные на нашем графике:
Найдём
нужные для расчёта данные на нашем графике:
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
После чего с помощью приведённых выше формул считаем коэффициенты:

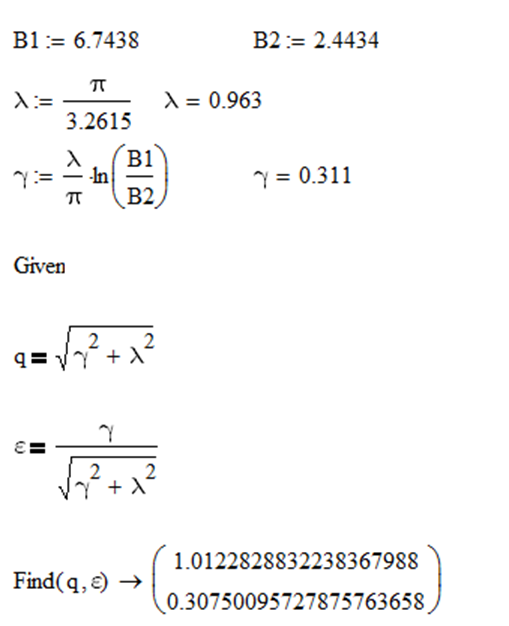
Видим, что коэффициенты приблизительно равны, подтверждая тем самым правильность расчётов.
1.7. Получение аналитических выражений переходной и весовой функции классическим методом.
Задана передаточная функция
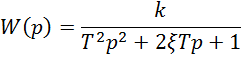
Записываем выражение в дифференциальном виде
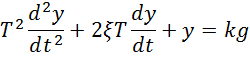
делим
левую и правую часть на ![]()
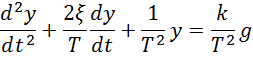
Записываем характеристическое уравнение
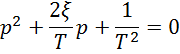
Корни для данного характеристического уравнения
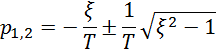
Введем обозначения
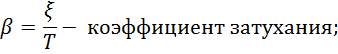
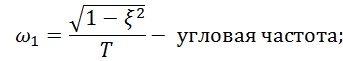
тогда
![]()
Записываем общее решение однородного дифференциального уравнения
![]()
где
![]()
![]()
Записываем систему уравнений
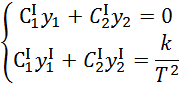
Теперь необходимо вычислить ![]()
![]()
![]()
![]()
Подставляем полученные выражения в уравнение
![]()
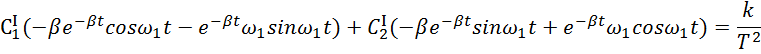
Из
первого уравнения найдём ![]()
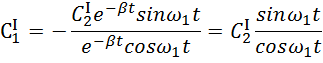
Подставляем во второе уравнение
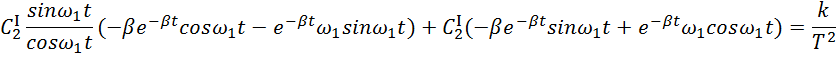
Вынесем ![]() за
скобки и преобразуем выражение
за
скобки и преобразуем выражение
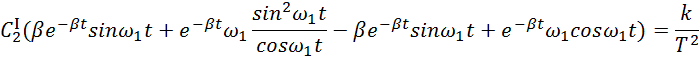
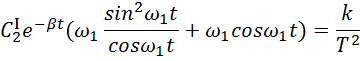
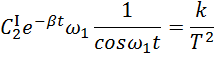
Отсюда
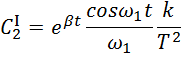
Найдем ![]()
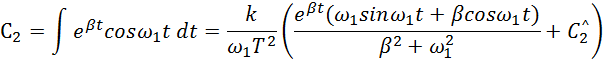
Находим ![]() из
первого уравнения
из
первого уравнения
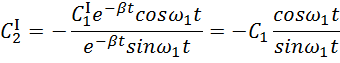
Подставляем во второе уравнение
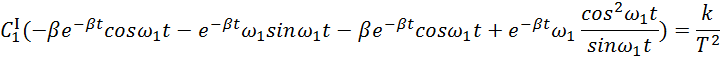
Выполнив сокращение получим
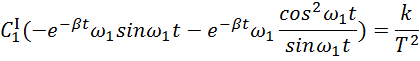
Упростим данное выражение
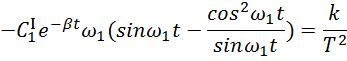
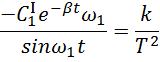
Отсюда
![]()
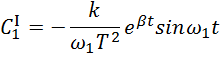
Интегрируем
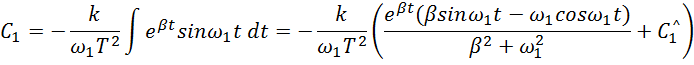
Записываем общее решение
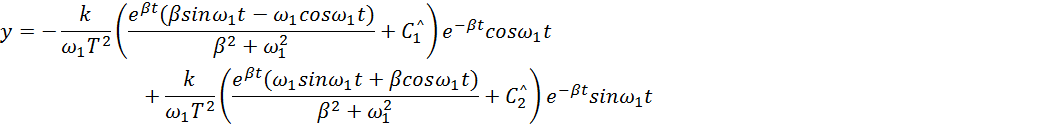
Выполним преобразование
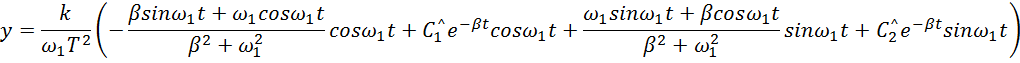
Преобразуем числитель
![]()
Тем самы получаем
Определяем
![]() ,
,
![]() исходя
из того что
исходя
из того что ![]()
Имеем
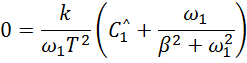
Отсюда
находим ![]()
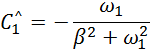
Для
нахождения ![]() возьмем
производную от y
возьмем
производную от y
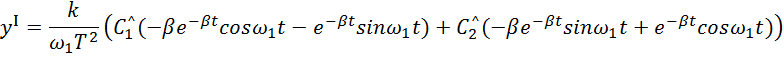
при t=0
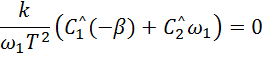
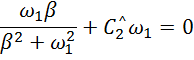
Отсюда
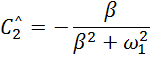
Подставляем в выражение y
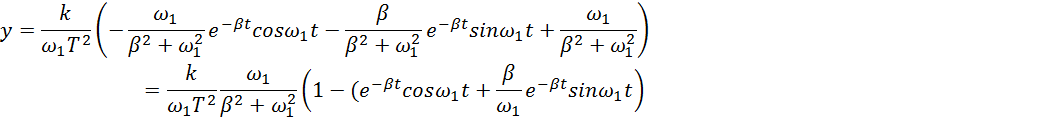
Рассмотрим отдельно
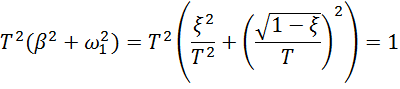
И окончательно
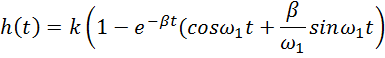
1.8. Получение аналитических выражений переходной и весовой функции операторным методом.
Задана передаточная функция
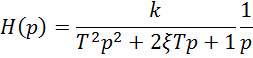
Корни для данного уравнения
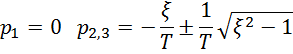
Введём обозначение
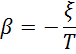
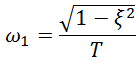
Найдём
![]()
Слагаемое,
которое соответствует корню ![]() ,
равно
,
равно ![]()
Найдем слагаемые, соответствующие комплексно-сопряженным корням
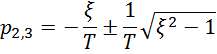
![]()
Найдем A и B
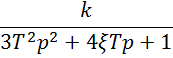
Подставим значение первого корня
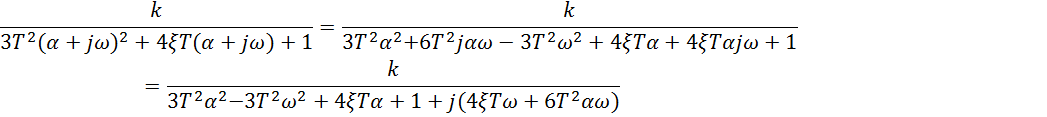
Введем обозначение
![]()
![]()
Преобразуем выражение
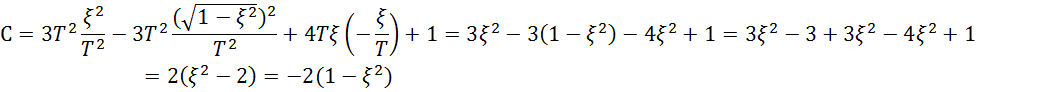
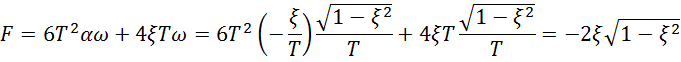
Возвращаемся к выражению
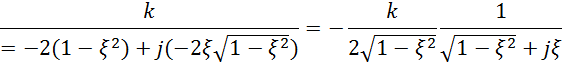
Преобразуем
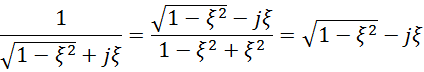
Обозначим
![]()
![]()
После чего получим
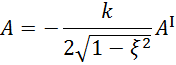
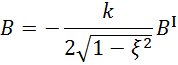
Запишем уравнение для переходной функции
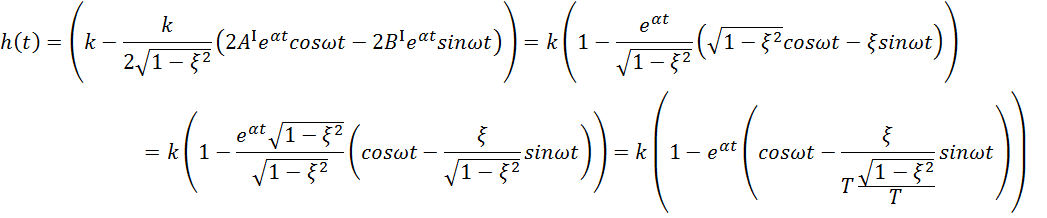
И окончательно
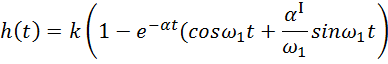
где 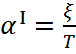
1.9. Описание процесса построения и сам график переходной и весовой функции.
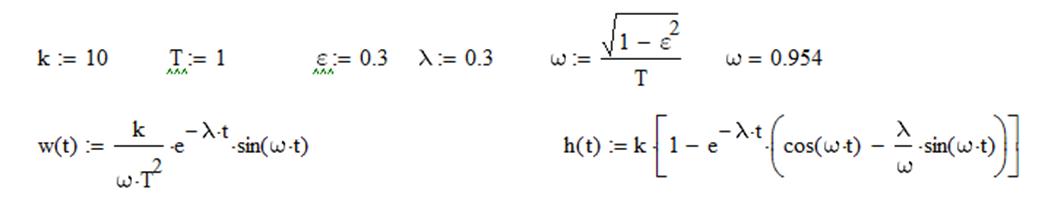 Построение
графиков выполнялось в вычислительной среде MathCAD. Для этого задаём параметры
звена и уравнения переходной и весовой функции, после чего строим графики.
Построение
графиков выполнялось в вычислительной среде MathCAD. Для этого задаём параметры
звена и уравнения переходной и весовой функции, после чего строим графики.
График переходной функции
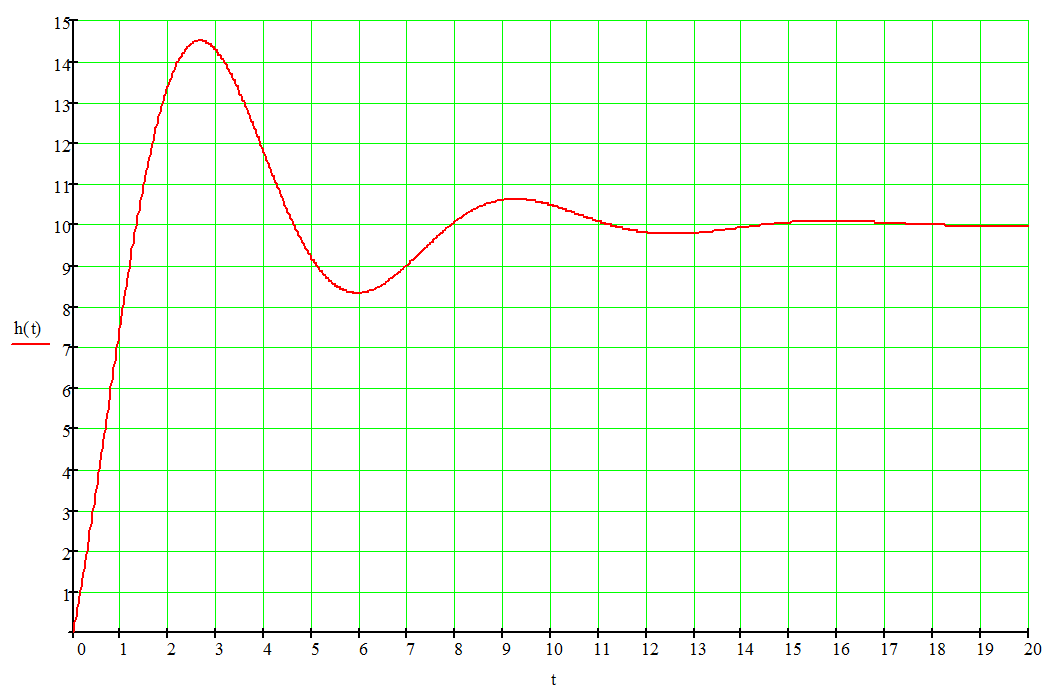 |
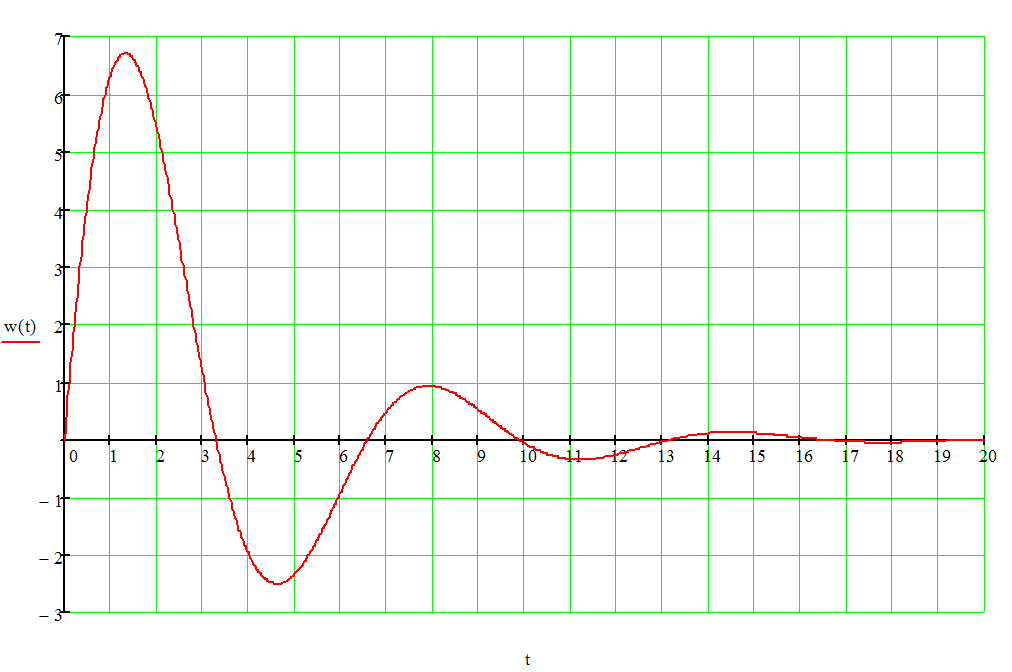 График
весовой функции
График
весовой функции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.