Основные понятия современной теории управления

1.  Основные понятия современной теории  управления.

                                   Оглавление

1.1.  Переменные состояния и уравнения состояния динамической

системы……………………………………………………………1

1.2.  Матричная передаточная функция………………………………5

1.3.  Понятия управляемости и наблюдаемости системы……………5

1.1. Переменные состояния и уравнения состояния динамической        системы.

Состояние динамической системы- это совокупность физических переменных характеризующих поведение системы в будущем при условии, что известны ее начальное состояние и приложенные воздействия.

Динамическая система может быть описана системой дифференциальных уравнений первого порядка

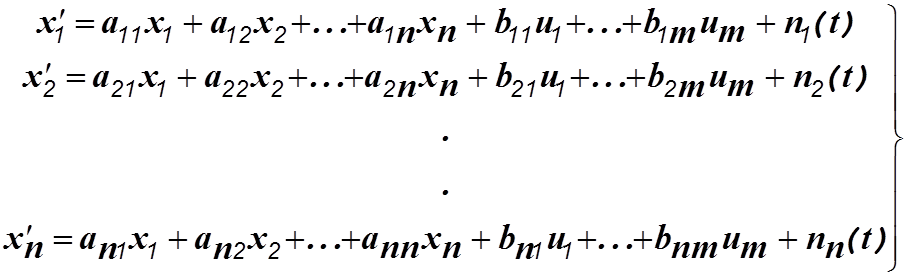
Запишем эту систему в матричной форме

                                                                   (1.1)

В этом выражении  X--матрица параметров (координат) состояния, А-матрица состояния, составленная из коэффициентов системы уравнений, B-матрица управления, U-матрица управляющих воздействий,  n(t)-вектор возмущений размерности

Все или только некоторые параметры состояния для использования в целях управления должны быть измерены приборами специальной измерительной системы. Поэтому для полного описания динамической системы  уравнение состояния (1.1) должно быть дополнено уравнением, связывающим переменные состояния 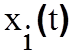 и выходные переменные измерительной системы 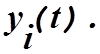 Эти выходные переменные в общем случае являются линейной комбинацией параметров состояния с некоторыми весами и связь между ними выражается  системой линейных алгебраических уравнений

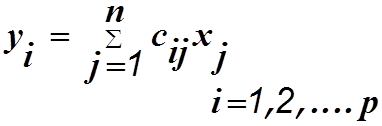                       (1.2)                                        

В векторно-матричной форме уравнение (1.2) можно записать следующим образом

                                                                                     (1.3)

Матрицу столбец Y= 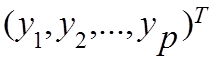  называют выходным вектором или вектором наблюдения. Матрица С размера   называется матрицей выхода или матрицей наблюдения.  

Решение векторно-матричного уравнения (1.1) при n(t)=0 можно найти так же, как и решение обыкновенного дифференциального уравнения 1-го порядка. Рассмотрим обыкновенное дифференциальное уравнение вида

                   

  В изображениях по Лапласу получим

                       

Отсюда

                         

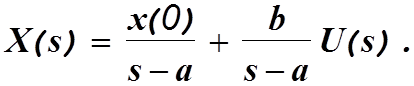
Использовав процедуру обратного преобразования Лапласа, получим

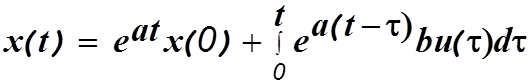                                          (1.4)

Решение векторного уравнения (1.1) определяется аналогично.

                        

Отсюда

                        

В этом выражении I-единичная  матрица. По аналогии с (1.4) запишем

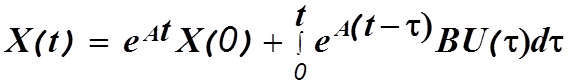                                      (1.5)

Функция 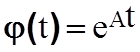   называется фундаментальной или переходной матрицей.

Методы вычисления фундаментальной матрицы.

а).Метод разложения в ряд.

           

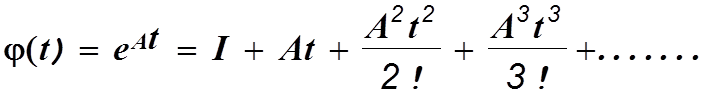
Ограничившись конечным числом членов ряда и произведя их суммирование, можно получить приближенное выражение для фундаментальной матрицы.

б).Метод, основанный на определении собственных значений матрицы состояния.

В соответствии с преобразованием Лапласа получим

          

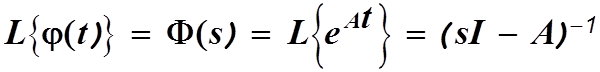
и следовательно

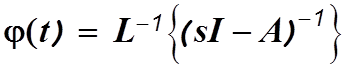                                                             (1.6)

Определение фундаментальной матрицы сводится к вычислению собственных значений матрицы состояния и последующему использованию процедуры обратного преобразования Лапласа.

в).Метод, основанный на теореме  Сильвестра.

 Предположим, что имеется некоторая функция f(A) от матрицы А, которую можно представить в виде степенного ряда

            

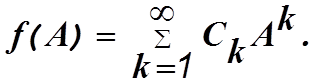
Допустим, что все собственные числа матрицы А различны. Тогда согласно теореме Сильвестра

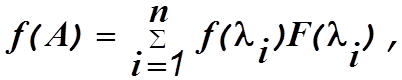                              где

                          

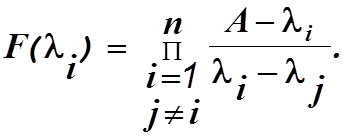
Здесь 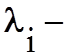   собственные числа матрицы состояния А.

В частном случае, когда 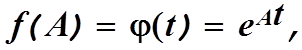  получим

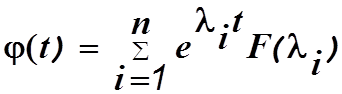                                                                 (1.7)

После определения фундаментальной матрицы строится решение  (1.5).

Часто возникает задача найти описание системы в понятиях пространства состояний, если известна ее передаточная функция в обычном понимании, т.е. в системе “вход-выход”. Пусть эта передаточная функция имеет вид

              

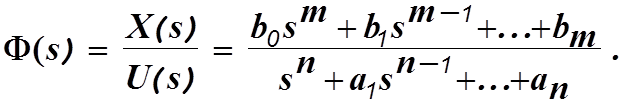
Дифференциальное уравнение в изображениях по Лапласу будет следующим

                         

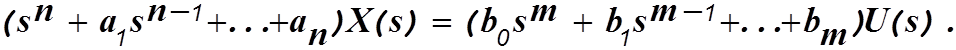
Допустим вначале, что  m=n.

Сделаем замену 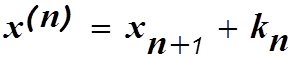  и перейдем к системе уравнений первого порядка.

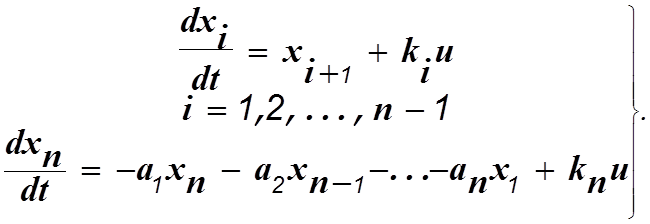                        (1.8)

Для определения неизвестных коэффициентов  проделаем следующие операции:

а) перейдем в системе (1.8) к изображениям по Лапласу при нулевых начальных условиях;

б) найдем характеристический определитель полученной алгебраической системы уравнений;

в)решим эту систему уравнений относительно переменной

г)учитывая, что      найдем выражения для x(s) и, приравнивая числитель полученного выражения числителю исходной передаточной функции, получим рекуррентные соотношения для определения коэффициентов  

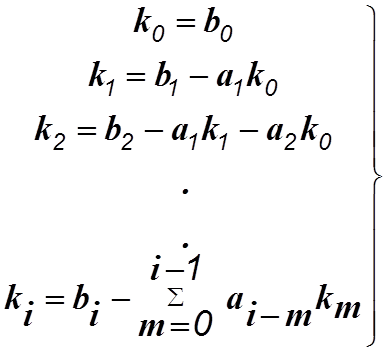                                               (1.9)

В практических приложениях всегда m<n и при использовании формул  (1.9) нужно полагать все коэффициенты от    до    включительно равными нулю.

При известных система уравнений (1.8) описывает динамику САУ в пространстве состояний.

1.2.Матричная передаточная функция.

Матричные уравнения (1.1) и  (1.2) в изображениях по Лапласу при n(t)=0 образуют систему

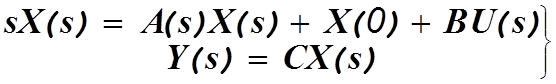                             (1.10)

При нулевых начальных условиях, исключая из системы X(s), получим

                         

Матрицу

                  ,                                   (1.11)

устанавливающую связь между вектором выхода Y(s) и вектором входа U(s) называют матричной передаточной функцией (МПФ).

1.3.Понятия управляемости и наблюдаемости  системы.

Управлять  состоянием системы  можно изменением вектора  , а наблюдать ее состояние можно измеряя вектор выхода   

Система называется управляемой, если она может быть переведена из произвольного состояния  в любое другое желаемое состояние  за конечный интервал времени  путем приложения кусочно-непрерывного входного воздействия

Рассмотрим уравнение состояния

        

Будем считать, что матрица А имеет все различные собственные значения. Определим матрицу собственных векторов V и осуществим линейное преобразование

                       

После подстановки в исходное уравнение, получим

                        

Умножим слева полученное выражение на

                         

Доказано, что  есть диагональная матрица   элементами которой являются собственные числа матрицы А.

                         

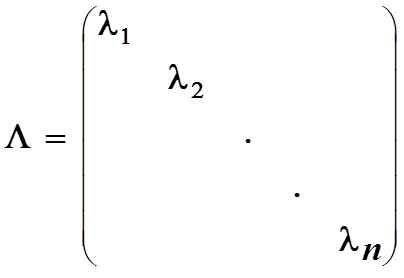
Тогда

                                                                    (1.12)

                                    

Уравнения (1.12) называются каноническими. Эта форма записи уравнений удобна тем, что в ней отсутствует  взаимосвязь между каноническими переменными состояния. Из (1.12) следует, что система, заданная в канонической форме управляема, если ни одна из строк матрицы не является нулевой. С физической точки зрения это означает, что в управляемой системе вектор управления воздействует на каждый параметр состояния. Это условие не выполняется, если хотя  бы одна строка вышеуказанной матрицы является нулевой. Рассмотренный критерий называется критерием управляемости Гильберта.

Доказана также другая формулировка критерия управляемости, не связанная с диагонализацией матрицы А.

Система является управляемой, если матрица управляемости 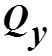 имеет ранг, равный n.

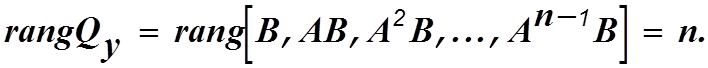          (1.13)

Если управляемость требует, чтобы каждое состояние системы было чувствительно к воздействию входного сигнала, то наблюдаемость требует, чтобы каждое состояние системы влияло на измеряемый выходной сигнал. Может  быть так, что некоторая переменная состояния     не связана непосредственно с выходом и по наблюдению выхода y  ее определить невозможно. Но для управления необходимо располагать сведениями о всех текущих значениях вектора состояния. Поэтому возникает вопрос: при каких условиях, наблюдая векторы входа и выхода, можно найти переменные состояния x?

Систему называют наблюдаемой, если по данным измерения или наблюдения векторов  и на конечном интервале времени     можно однозначно определить начальное состояние Систему называют полностью наблюдаемой, если наблюдаемы все ее состояния в любые моменты времени.

После диагонализации исходной системы можно записать

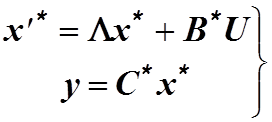                                                        (1.14)

Здесь    

Исходя из выше данного определения можно заключить, что система (1.14) наблюдаема, если ни один из  столбцов матрицы  не является нулевым.

Таким образом система наблюдаема, если все ее состояние можно непосредственно или косвенно определить по выходному вектору системы. Ненаблюдаемая система не может быть идентифицирована в пространстве состояний. т.к. невозможна идентификация параметров, относящихся к ненаблюдаемым состояниям.

Система полностью наблюдаема, если ранг матрицы наблюдения R равен порядку системы n.

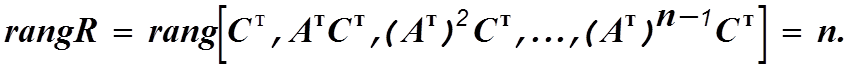     (1.15)

Очевидная аналогия между критериями управляемости и наблюдаемости позволяет сделать вывод об их дуальности. Назовем два объекта  и дуальными, если их можно описать соответственно уравнениями:

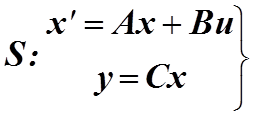                                                                            (1.16)

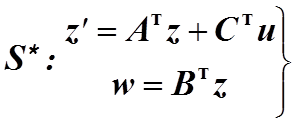                                                                     (1.17)

Из уравнений (13),(15), (16) и (17) следует, что если  управляема в , то наблюдаема в  и наоборот.

Таким образом, наблюдаемость одной из систем можно проверить анализом управляемости дуальной ей системы.

В заключение отметим, что понятия управляемости и устойчивости не связаны между собой. Устойчивость в пространстве состояний также определяется корнями характеристического уравнения системы (собственными числами матрицы состояния)

                                                            .                                                              (1.18)