11. Закон распределение Стьюдента и интеграл Стьюдента
Многие задачи статистики приводят к случайной величине вида
![]() ,
,
где x и h – независимые случайные величины, причем x – нормально распределенная случайная величина с параметрами Mx = 0 и Dx = 1, а h распределена по закону c2 c k степенями свободы.
Закон распределения случайной величины t называется законом распределения Стьюдента с k степенями свободы.
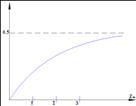
График плотности распределения для закона Стьюдента схематически изображен на рисунке 3. Кривая плотности распределения схожа с аналогичной кривой для нормального распределения.
Таблицы распределения Стьюдента позволяют при данном числе степеней свободы k по вероятности q определить значение tq, для которого выполняется соотношение P(|t| > tq) = q. Фрагмент такой таблицы представляет собой таблица 2.
|
q k |
0,1 |
0,05 |
... |
0,01 |
0,005 |
... |
|
1 |
6,314 |
12,71 |
... |
63,57 |
318 |
... |
|
... |
... |
... |
... |
... |
... |
... |
|
12 |
1,782 |
2,179 |
... |
3,055 |
3,428 |
... |
|
... |
... |
... |
... |
... |
... |
... |
Плотность вероятностей распределения Стьюдента описывается функцией
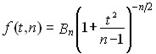 ,
,
где t - текущая переменная;
п — объем выборки;
В — величина, зависящая лишь от п.
Распределение Стьюдента имеет только один параметр: d.f. -число степеней свободы (иногда обозначается k).
12. Интеграл Лапласса.
Подставим
в интеграл (5) функцию нормального распределения ![]() ,
тогда:
,
тогда: ![]() . Пусть
. Пусть 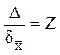 (6),
при n=const,
(6),
при n=const, ![]() , z – безразмерная
величина.
, z – безразмерная
величина.
Тогда
max значение ![]() , т.е. границей доверительного
интеграла будет max значение параметра z.
, т.е. границей доверительного
интеграла будет max значение параметра z. ![]() (7), тогда:
(7), тогда: 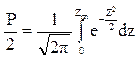 (8)
интеграл Лапласа.
(8)
интеграл Лапласа.
Значение
интеграла Лапласа определяет половину доверительной вероятности и
соответствующее ей значение доверительного интеграла![]() .
Значение этого интеграла зависит от верхнего предела (от
.
Значение этого интеграла зависит от верхнего предела (от![]() ).,
он не вычисляется в элементарных функциях.
).,
он не вычисляется в элементарных функциях.
![]()
 При
При ![]() ,
, ![]()
Вывод:
max возможное
значение погрешности случайного характера, т.е. подчиняющегося теории ошибок не
должно превышать значение ![]() - это цена max значения
погрешности случайного характера случайной величины
- это цена max значения
погрешности случайного характера случайной величины ![]() .
Для оценки абсолютной погрешности Х принято равенство
.
Для оценки абсолютной погрешности Х принято равенство ![]() (9).
(9) – критерий выявления промахов. При обнаружении промахов, значения
исключаются и нормированные характеристики (
(9).
(9) – критерий выявления промахов. При обнаружении промахов, значения
исключаются и нормированные характеристики (![]() )
должны быть рассчитаны заново.
)
должны быть рассчитаны заново.
13. Алгоритм статической обработки серии прямых измерений
Если
![]() , то сама измеряемая величина и её
погрешность распределяются по нормальному закону, т.е.
, то сама измеряемая величина и её
погрешность распределяются по нормальному закону, т.е. ![]() имеет
центр распределения. При малой выборке
имеет
центр распределения. При малой выборке ![]() и
и![]() отклоняются от функции Гаусса и
подчиняются другому закону, называемой функцией распределения student. t=коэффициент student
отклоняются от функции Гаусса и
подчиняются другому закону, называемой функцией распределения student. t=коэффициент student ![]()
![]()
![]()
![]()
![]()
Выявляем
промахи ![]()
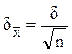
![]() - математическое ожидание.
- математическое ожидание.
14. Погрешность косвенных измерений.
Пусть u = f( x, y) функциональная зависимость между измеряемой величиной u и величинами x y , ,... , значения которых найдены прямыми измерениями. Действительное значение <u > определяется как:
![]()
Получим выражение для погрешности Δu. Если зафиксировать значения всех аргументов кроме одного, например x, то приращение функции при изменении ее аргумента имеет вид:
![]()
Если значение Δx мало, то в интервале [<x> - Δx , <x> + Δx ] функцию u =f (x) можно считать линейной и
![]()
Величина Δx u характеризует погрешность Δu, обусловленную погрешностью Δx . Аналогично определяются составляющие погрешности Δu, вносимые другими аргументами. Полная погрешность Δu косвенных измерений u вычисляется либо с помощью квадратичного суммирования либо суммирования по модулю ее составляющих, вносимых каждым аргументом:

Соотношения (12) применяется в том случае, когда выполняются два условия. Во-первых, погрешность аргументов обусловлена влиянием многих факторов, среди которых нет преобладающего фактора. Во-вторых, погрешности аргументов статистически не связаны.
15. Совместное измерение двух и большего количества измеренных величин.
16. Основная задача совместного измерения и его погрешность.
17. Виды электрических сигналов и их осциллограммы.
![]()
![]()
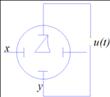
 Графические
переменные во времени сигналы осциллограммы, поскольку такую картинку мы
наблюдаем на экране осциллографа, когда исследуем
Графические
переменные во времени сигналы осциллограммы, поскольку такую картинку мы
наблюдаем на экране осциллографа, когда исследуем ![]() .
.
Импульсы…
линейнонарастающего напряжения такую форму вырабатывает осциллограф ГЛИН для
создания горизонтальной развертки ЭЛТ, причем движение Эл. луча равномерное,
т.е. ![]() в противном случае реальная
зависимость исследуемых сигналов
в противном случае реальная
зависимость исследуемых сигналов ![]() будет с
искажением.
будет с
искажением.
Переменные сигналы определяются следующими нормированными метрологическими характеристиками:
Среднее
за период значение периодического сигнала напряжения ![]() ,
где
,
где ![]() -мгновенное значение напряжения
-мгновенное значение напряжения ![]() - гармонический сигнал.
- гармонический сигнал.![]()
Среднее
выпрямленное значение напряжения ![]()

Среднее
квадратичное (действующее) значение напряжения 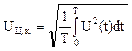
Отметим,
что для гармонич. ср. за период за период значение ![]()
![]()
![]()
![]()
![]() Среднее
квадратичное значение сигнала напряжение измеряется вольтметром переменного
тока, поэтому оно называется действующим значением
Среднее
квадратичное значение сигнала напряжение измеряется вольтметром переменного
тока, поэтому оно называется действующим значением
При
подстановке в п. 3 гармонического сигнала и вычисления сигнала имеем 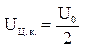 .
.
18. Характеристики периодических сигналов.
Под
электрическим сигналом понимают временную зависимость U(t) или I(t) нагрузки.
Графически переменные электрических сигналов называются осциллограммами.
Характеристики: 1)средне за период значение периодического сигнала напряжения 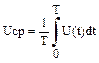 2)среднее выпрямленное
значение напряжения
2)среднее выпрямленное
значение напряжения 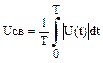 3)действующее
значение напряжения
3)действующее
значение напряжения 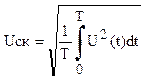 -
измеряется вольтметром переменного тока
-
измеряется вольтметром переменного тока
19. Аналоговые электроизмерительные приборы.
АЭиП являются приборами непрерывного действия и содержат неподвижную со шкалой и подвижную часть со стендом.
Для поворота подвижной части и соответственно поворота стрелки под воздействием измеряемой величмны (x) (U;I;P;W)
Согласно
уравнению Лагранжа в различный момент находится как: 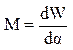 ,
производная от энергии по углу поворота
,
производная от энергии по углу поворота ![]() ,
где W –
электромагнитная энергия, в частности при работе АЭиП используются следующие её
виды.
,
где W –
электромагнитная энергия, в частности при работе АЭиП используются следующие её
виды.
![]() ~
~![]() -
индуктивная энергия (8)
-
индуктивная энергия (8)
![]() ~
~![]() -
электрическая энергия (9)
-
электрическая энергия (9)
Энергия,
связанная с взаимоиндуктивностью действующей катушки ![]() ~
~![]() (10)
(10)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.