Оптимальные системы автоматического управления, страница 3

Изопериметрическая задача путем введения множителей  сводится к задаче на безусловный экстремум следующего функционала. Из этого следует, что для решения изопериметрической задачи требуется составить уравнение Эйлера-Лагранжа для функционала вида 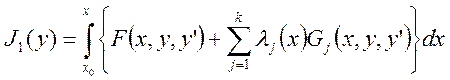(1):

   (1)

Произвольные постоянные в общем решении уравнений Эйлера и   определяются из граничных условий:

 

Задача Майера

Эта задача входит в класс задач на условный экстремум и формулируется следующим образом: Среди всех кривых, кусочно-гладких, которые удовлетворяют условиям связи:

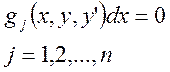  (1)

и граничным условиям:

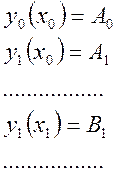   (2)

Требуется найти такую функцию, у которой первая составляющая имеет при  экстремум.

Задача Майера может быть сведена к задаче Лагранжа на условный экстремум, которая формулируется следующим образом: среди кусочно-гладких векторных функций , которые удовлетворяют уравнениям связи (1) и граничным условиям (2), требуется найти такую функцию, при которой функционал:

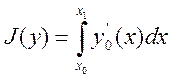  (3)

достигает экстремума.

В свою очередь путем введения новой функции:

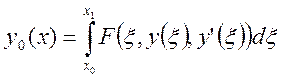
Задача Лагранжа может быть сведена к задаче Майера. Они эквивалентны.

Заменим вспомогательный функционал:

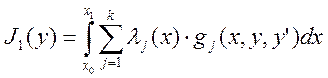  (4)

Задача сводится к безусловному экстремуму, и уравнение Эйлера-Лагранжа для функции будет иметь вид:

  (5)

Произвольные постоянные, возникающие при интегрировании уравнений (1) и (5) могут быть определены из условий (2). К уравнению (5) надо добавить k уравнений связи (1).

Задача Больца

В этой задаче необходимо определить кусочно-гладкую функцию, удовлетворяющую условию связей вида 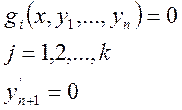(1):

  (1)

Граничным условиям:

 

       (2)

  

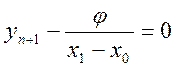
и доставляющую экстремум функционалу:

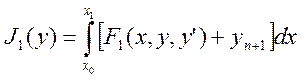 (3)

Из уравнений связи следует, что , тогда и, следовательно:

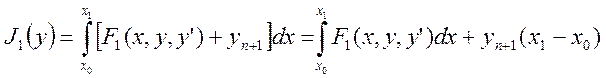
Из последнего равенства следует:

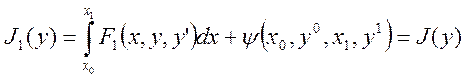
Здесь учтены граничные условия (2).

В свою очередь задача Лагранжа является частным случаем задачи Больца, когда:

.

Итак, если теперь ввести специальные множители , задача Больца также сводится к задаче на безусловный экстремум функционала:

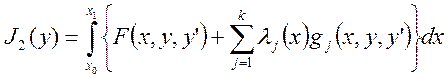  (4)

Для определения неизвестных функций  и множителей Лагранжа  нужно составить уравнение Эйлера-Лагранжа:

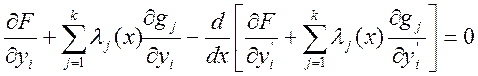    (5)

которое удовлетворяет условиям связи:

 

Произвольные постоянные, которые возникают при интегрировании уравнения (5), могут быть найдены с помощью граничных условий (2).

Для граничных условий (2) необходимо использовать условие трансверсальности:

  (6)

Здесь:

Тождество должно иметь место для любых значений дифференциалов .

Линейные системы. Квадратичный критерий качества процессов управления

Будем считать, что объект управления описывается системой дифференциальных уравнений:

  (1)

Здесь:

X – n-мерный вектор состояния ОУ;

U – m-мерный вектор управляющих функций;

A – матрица размера (матрица динамики ОУ);

B – матрица (матрица коэффициентов передачи).

Управление динамическим объектом (1) должно быть таким, чтобы минимизировать критерий качества ОУ в функционал:

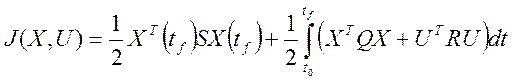  (2)

Здесь  и  не отрицательно определенные симметричные матрицы размера , которые удовлетворяют условиям:

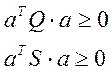
Эти два неравенства должны выполняться для любого n-мерного вектора.

Далее, - положительно определенная матрица , то есть это симметричная матрица, которая удовлетворяет условию:

для любого m-мерного вектора .

Мы считаем, что  - начальное значение и  - конечное значение вектора состояния ОУ.

Вводим в рассмотрение вспомогательный функционал:

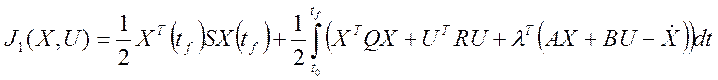  (3)

Теперь вводится в рассмотрение вспомогательная скалярная функция:

  (4)

Вводим вспомогательную функцию, которая имеет название – гамильтониан. В этом случае функционал запишется:

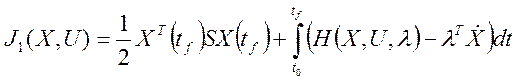 (5)

Теперь рассмотрим интеграл: .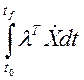

Берем интеграл по частям:

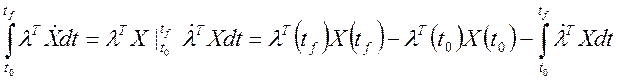
Теперь функционал (5) запишется в виде:

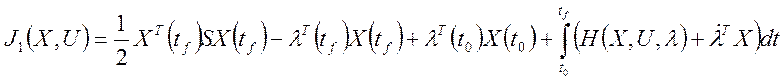  (6)

Теперь рассмотрим вариацию этого функционала, которая вызвана вариацией управляющей функции  и вектора . При этом считаем, что если начальное значение времени фиксировано, то фиксировано также и конечное значение времени .

Выражение для вариации функционала:

  (7)

Выберем вектор таким образом, чтобы коэффициенты при вариациях  и  были равны нулю. Тогда получаем уравнение для определения :

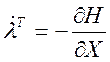 (8)

Граничные условия для системы уравнений (8):

  (9)

Так как:

  (10)

тогда в этом случае вариация функционала запишется:

  (11)

Сделаем следующее замечание: вспомогательный функционал  совпадает с исходным функционалом на решениях системы уравнений (1). Поэтому, если  достигает минимума, то минимума достигает и функционал . Если  достигает минимума, то его вариация должна быть равна нулю.

То есть должно выполняться условие:

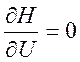
   (12)

Приведем сведения из линейной алгебры, которые мы будем использовать в дальнейшем:

   

  

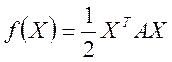
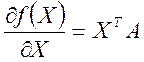
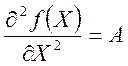
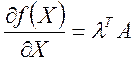
На основании этих формул получаем следующее:

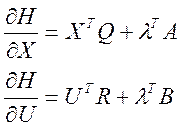
Чтобы найти вектор управляющих функций, которые доставляют экстремум функционалу (2) или критерию качества, нужно решить систему дифференциальных уравнений:

 (13)

(14)

где управляющая функция   определена из условия:

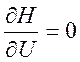
Транспонированный вектор управляющей функции определяется равенством:

Или:

 (15)

Здесь следует отметить, что граничные условия для уравнений (13) и (14) разделены. Одно из них  задано на левом конце траектории , другое  задано на правом конце .

Теперь, с учетом этого, запишем следующие дифференциальные уравнения, которые определяют оптимальное управление:

 (16)

     (17)

где заданы граничные условия:

 и   (18)

Это так называемая двухточечная краевая задача.

Решение линейной двухточечной краевой задачи методом прогонки

Идея метода прогонки содержится в самом соотношении:

Попытаемся перенести (прогнать) граничные условия к начальному моменту времени . В результате чего получим начальное значении , и затем, так как нам будет известно начальное состояние системы  и значение , то можно выполнить интегрирование системы уравнений: