Наблюдение объектов при случайных помехах

4. Наблюдение объектов при случайных помехах.

Требуемым выходным сигналом W(t)  проектируемой системы является результат выполнения некоторой операции L над полезным сигналом S(t).

                                                                     (4.1)
Действительным выходным сигналом системы является некоторая случайная функция W^*(t), которая представляет собой результат преобразования данной системой входной функции Z(t)=S(t)+N(t), где N(t)- случайная помеха.

                                                                 (4.2)
Здесь А- оператор системы. Ошибка системы определится выражением

                                                    (4.3)
Оптимальной системой, предназначенной для выполнения операции L над входным сигналом, будет такая система, ошибка которой имеет минимальное в определенном смысле значение.

Ошибка, определяемая выражением (4.3), является случайной функцией времени. Поэтому она не может непосредственно служить оценкой точности системы и естественно в качестве этой меры точности взять ее в вероятностном смысле среднее значение. Так как знак ошибки в большинстве случаев нас не интересует, то за характеристику точности принимают математическое ожидание среднего квадрата ошибки

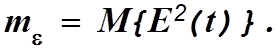                                                             (4.4)
Положительное значение корня квадратного  из этой величины называется средним квадратическим отклонением (СКО).

Критерий минимума СКО является с математической точки зрения простейшим и обычно приводит к наиболее простым методам определения оптимальных систем. Важным обстоятельством является то, что при нормальном распределении полезных сигналов и помех оптимальная линейная система, найденная по критерию минимума СКО, оказывается оптимальной и с точки зрения других критериев. 

                         Оглавление

4.1. Общее условие минимума СКО……………………1

4.2. Интегральное уравнение Винера- Хопфа………….4

4.3. Уравнение нестационарной фильтрации Калмана-

        Бьюси………………………………………………..6

    4.3.1. Вывод дифференциального уравнения опти-

           мального фильтра Калмана – Бьюси…………….6

    4.3.2. Определение оптимального коэффициента

             усиления фильтра………………………………. 8

    4.3.3. Анализ уравнений оптимальной фильтрации ..11

4.1.Общее условие  минимума  СКО.

Предположим, что в некотором классе систем R требуется найти оптимальную систему, для которой СКО имеет минимально возможное значение. Обозначим через А оператор оптимальной системы в классе R, а через B-оператор любой системы в этом же классе. Сигналы систем можно записать в виде

                .                                                         (4.5)

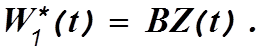                                                           (4.6)
Вычислим СКО произвольной системы и для краткости опустим аргумент t.

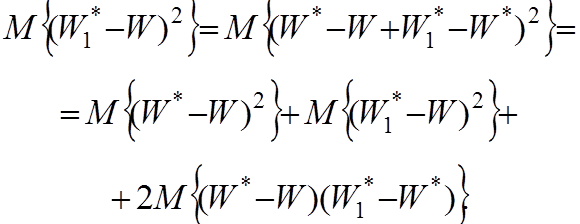   (4.7)
Предположим теперь, что в классе R имеется  такая система с оператором А, выходная переменная которой W^* удовлетворяет условию

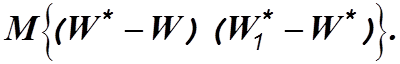                                                         (4.8)
Равенство (4.7) примет вид

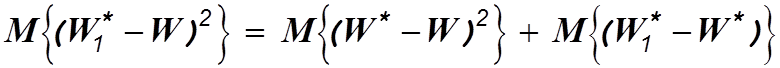.     (4.9)
Правая часть этого равенства представляет собой сумму двух неотрицательных слагаемых. Отбрасывая второе слагаемое, получим

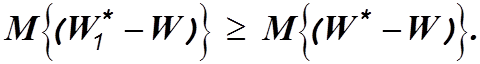                                             (4.10)
Следовательно, СКО системы, выходная переменная которой удовлетворяет равенству (4.8) для выходных переменных W₁^* всех систем класса R не может быть больше СКО какой-нибудь другой системы класса R ,т.е. система , удовлетворяющая равенству (4.8) всегда является оптимальной. Условие (4.8) является , таким образом, достаточным условием минимума СКО.

Рассмотрим схему, представляющую собой параллельное соединение некоторых систем B_i, принадлежащих классу R, с весовыми коэффициентами С_i.

 

              B₁         C₁             W₁^*

 

             B₂         C₂  W₂^*  +               W₀^*

 

                                                        Рис.4.1. Параллельное соединение

              B_n         C_n             W_n^*                    систем В_i

Для этой системы можно записать

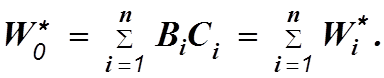                                                (4.11)
Будем считать, что множество, образованное выходными сигналами всех систем класса R, приведенных на рисунке 4.1., образует линейное пространство. Это означает, что любая линейная комбинация элементов этого множества также принадлежит этому множеству и, следовательно, эта линейная комбинация является выходной величиной системы класса R. В этом случае разность W₁^*-W^* также является выходной переменной произвольной системы класса R и ее можно обозначить как W₁^*. Тогда достаточное условие минимума СКО может быть записано в виде

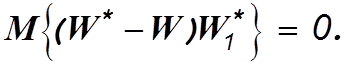                                                   (4.12)
Докажем теперь, что условие (4.12) является не только достаточным, но и необходимым. Для этого нужно доказать, что при невыполнении условия (4.12) величина W^* не может быть выходной переменной оптимальной системы. Предположим, что в классе R существует система с оператором В₀, для выходной переменной которой W₀^*  достаточное  условие минимума СКО не выполнено (рис.4.2).

                             W^*

             A              -              W₁^*

 

                     W₀^*

             B₀              a          

                     Рис.4.2.
Для определенности рассмотрим случай, когда

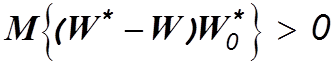                                                    (4.13)
Покажем, что коэффициент усиления  a всегда можно выбрать так, что система, показанная на рисунке 4.2, была лучше предполагаемой оптимальной в случае выполнения неравенства (4.13) или противоположного неравенства. Из рисунка следует

           
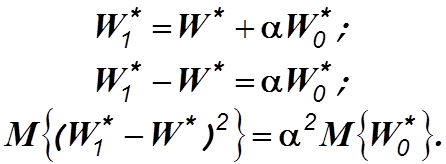
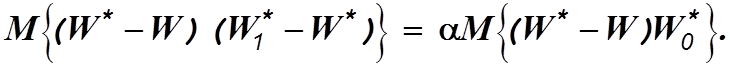
Подставляя эти выражения в (4.7), получим

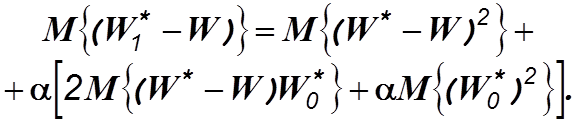                     (4.14)
Если взять достаточно малое по абсолютной величине отрицательное значение a, то при выполнении неравенства (4.13) выражение в квадратных скобках будет положительным и, следовательно, второе слагаемое в правой части (4.14) будет отрицательным. Отбрасывая это слагаемое, мы получим