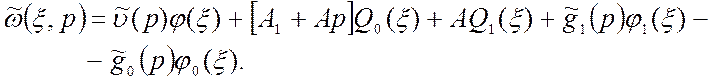 (1.73)
(1.73)
При структурном представлении распределенный объект с передаточной функцией W(x,ξ,p), входное воздействие которого описывается выражением (1.73), можно представить в виде рис.1.6.
Перенесем сумматор через звено с передаточной функцией W(x,ξ,p) (рис.1.7). На рис.1.7 введены обозначения:
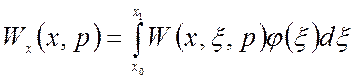 ;
(1.74)
;
(1.74)
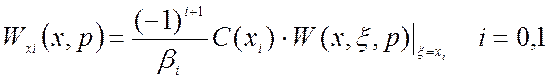 ; (1.75)
; (1.75)
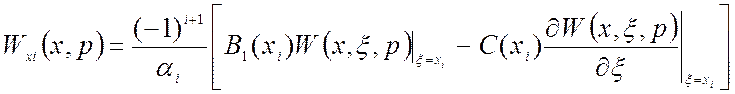 . (1.76)
. (1.76)
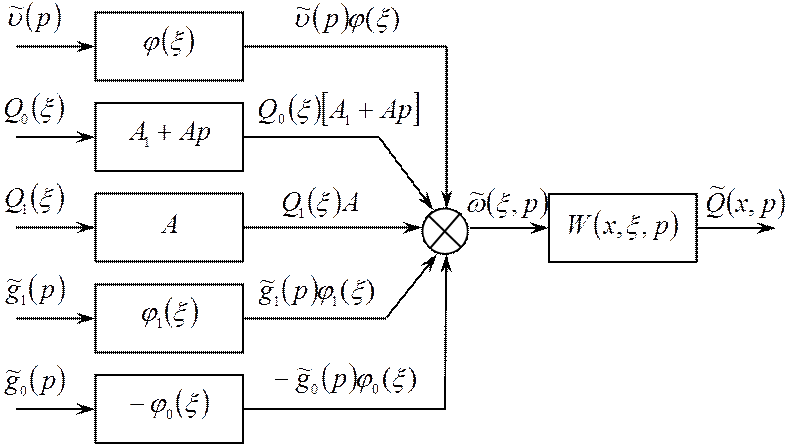
Рис.1.6 – Структурное представление распределенного блока
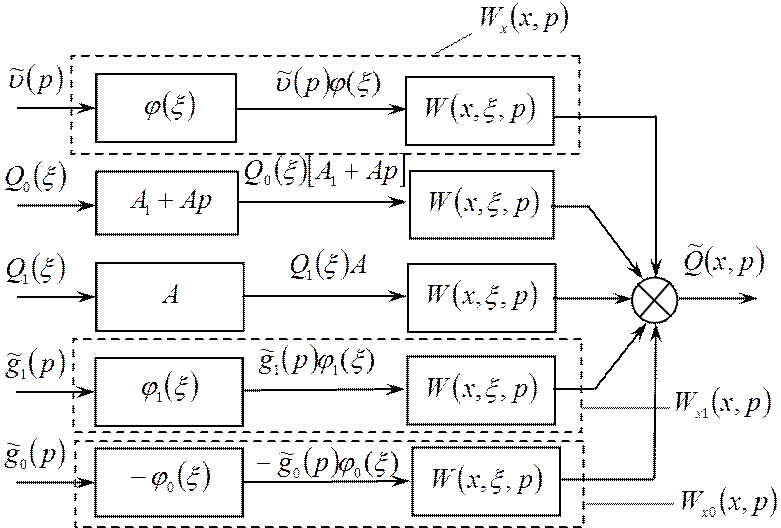
Рис.1.7 – Преобразование структурного представления объекта
Выражение (1.75) используется для второй и третьей краевой задачи, а (1.76) - для первой краевой задачи.
Таким образом, в трех случаях из пяти удается упростить структурное представление распределенного блока, используя понятие передаточной функции х-блока.
В результате получим представление согласно рис.1.8.
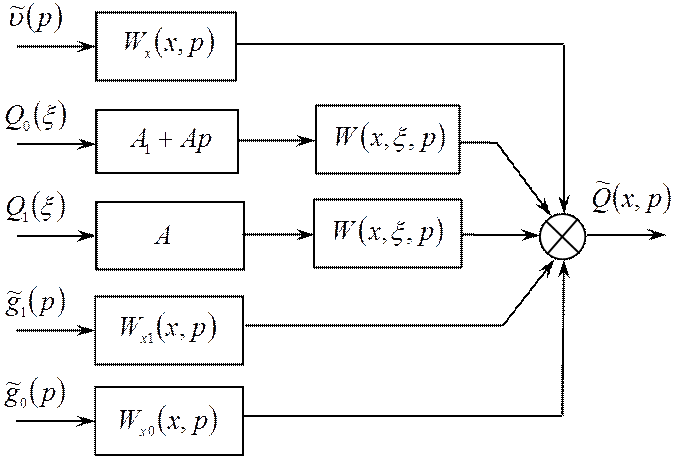
Рис.1.8 – Представление распределенного объекта с передаточными
функциями х-блока
Выходную распределенную величину тогда можно найти следующим образом:
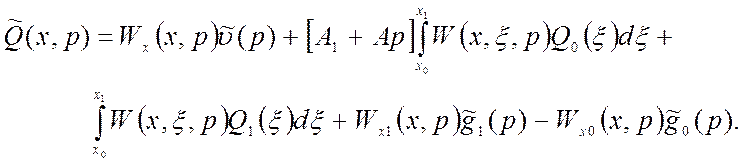 (1.77)
(1.77)
Необходимо подчеркнуть, что сказанное применимо для случая, когда входной воздействие может быть представлено согласно выражению (1.68). В противном случае, когда используется входное воздействие в виде распределенного управления φ(ξ) при фиксированном характере изменения во времени (ступенчатое или импульсное), переход к х-блоку не осуществляется и выполняются преобразования аналогично начальным распределениям Q0(ξ) и Q1(ξ).
Все слагаемые стандартизирующей функции также условно можно разбить на управляющие и возмущающие. В первом случае могут рассматривать входные (внутренние) или граничные управления, а во втором – начальные распределения и прочие внешние возмущения, не используемые в качестве управляющих воздействий. Поэтому можно в аналогии с ССП судить о передаточной функции по управлению и передаточной функции по возмущению.
В практических случаях часто формулируются задачи, когда отдельными слагаемыми в стандартизирующей функции можно пренебречь в силу равенства нулю входного воздействия, начальных или граничных условий. Тогда существенно упрощается и структурное представление ОРП.
2 Основные уравнения математической физики
2.1 Уравнения поперечных колебаний струны
Рассмотрим струну длиной l, которая в положении равновесия находится вдоль оси Ох. Ее поперечные колебания в каждый момент времени t для каждой точки х (0≤х≤l) характеризуется вектором смещения Q(x,t) и описывается уравнением вида:
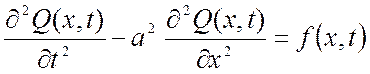 , (2.1)
, (2.1)
где а – волновая скорость, м/с;
f(x,t) – удельная сила (сила, действующая на единицу массы струны), м/с2.
Волновая скорость определяется согласно выражению:
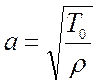 , (2.2)
, (2.2)
где Т0 – сила натяжения струны, Н;
ρ – линейная плотность (масса, приходящаяся на единицу длины струны), кг/м.
Удельная сила, в свою очередь, может быть представлена в виде:
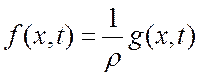 , (2.3)
, (2.3)
где g(x,t) – линейная плотность внешней силы, Н/м.
Если внешней силы нет f(x,t)=0, получаем уравнение свободных колебаний струны:
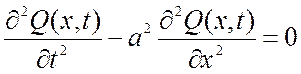 . (2.4)
. (2.4)
Для выбора начальных условий к данной задаче необходимо задать:
– профиль начальных смещений струны:
![]() ; (2.5)
; (2.5)
– профиль начальных скоростей:
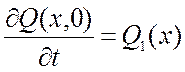 . (2.6)
. (2.6)
Также необходимо задать граничные условия (условия на концах струны).
1) Если концы струны закреплены, то имеем следующие граничные условия:
![]() ; (2.7)
; (2.7)
![]() . (2.8)
. (2.8)
2) Если концы струны свободны, т.е. могут свободно перемещаться по прямым, параллельным направлению отклонения Q(x,t), то граничные условия имеют вид:
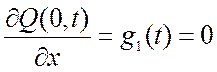 ; (2.9)
; (2.9)
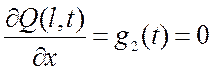 .
(2.10)
.
(2.10)
3) Если концы струны закреплены упруго, т.е. каждый конец испытывает со стороны заделки сопротивление, пропорциональное отклонению и направленное противоположно ему, то ГУ:
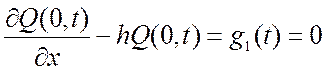 ;
(2.11)
;
(2.11)
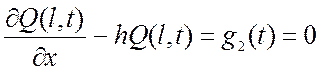 ,
(2.12)
,
(2.12)
где h=k/T0;
k – коэффициент упругости упругого закрепления концов струны.
4) Если концы струны двигаются в поперечном направлении по заданным законам, то ГУ:
![]() ;
(2.13)
;
(2.13)
![]() ,
(2.14)
,
(2.14)
где μ1(t), μ2(t) - определяют закон движения концов.
Пример 1.
Движение струны, натянутой и закрепленной в двух точках на расстоянии l, начинается посредством смещения струны в положение у(х)=a·sin(πx/l), из которого струну отпускают в момент времени t=0. Сформулировать краевую задачу для данного условия.
Функция Q(x,t), описывающая поперечные смещения струны определяется уравнением:
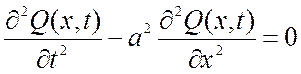 .
.
Поскольку концы струны закреплены, имеем граничные условия вида (2.7), (2.8):
![]() ;
; ![]() . Начальные
условия представляются в виде:
. Начальные
условия представляются в виде:
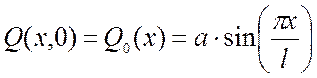 ;
;
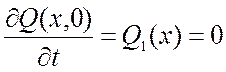 .
.
Пример 2.
Сформулировать краевую задачу о колебаниях однородной струны (0<x<l), закрепленной на концах, под действием внешней непрерывно распределенной силы с плотностью g(x,t)=Asin(ωt), где ω≠(kπa/t) (k=1,2…). Начальные условия нулевые.
Функция Q(x,t), описывающая колебания струны определяется уравнением:
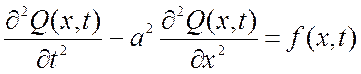 ,
,
где 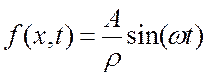 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.