Кодовые дешифраторы: Методические указания к практическим занятиям, страница 3

Из выражений (2) видно, что элемент комбинации <а0> входит в проверки р2, pl и не входит в проверку р0. Это означает, что ошибка на позиции ,где располагается элемент <а0>, нарушит 3-ю и 2-ю проверки, но не нарушит 1-ю проверку. То есть p2=p1=1; р0=0, тогда проверочное число будет иметь вид <110>, а опознаватель ошибки в a0 → p2p1p0. Будем обозначать буквами Z с десятичным индексом i, значение которого численно равно десятичному эквиваленту двоичного проверочного числа. Тогда опознаватели одиночных ошибок примут вид:

z6=р2p10 - для а0,

z5=p21р0 - для a1,                                          (6)                                              z4=2p1p0 - для a2.

Очевидно, результаты исправления ошибок можно представить выражениями:

α0=ā0z6; α1 = ā1z5; α2= ā2z3;                            (7)

где a0, a1 и а2 - «исправленные» информационные элементы (и, или переменные).

Нетрудно убедиться, что опознаватель вида z0=p2p1p0 соответствует отсутствию ошибок на позициях элементов а2, а1, а0, к1, к2, к3, а две ошибки могут привести к трансформации переданного сообщения, так как опознаватель 2-кратной ошибки совпадает с одним из опознавателей (6), и будет исправлена несуществующая «ошибка». А чтобы их обнаружить, необходимо запретить декодирование комбинаций <α2α1α0> при условии, что проверка (6) не нарушена и опознаватель z0 не равен лог.1. Или то же самое условие в алгебраической форме:

v=                                                (8)

Логическое выражение (8) является аналогом (4), но для случая исправления ошибок. Функциональная схема декодирующего устройства кода Хэмминга, исправляющего одиночные ошибки, приведена на рис.6. Работу такого ДШ легче уяснить в сравнении с работой ДШ рис.5. Аналогичным образом строятся ДШ кодов Хэмминга с большей длиной комбинации.

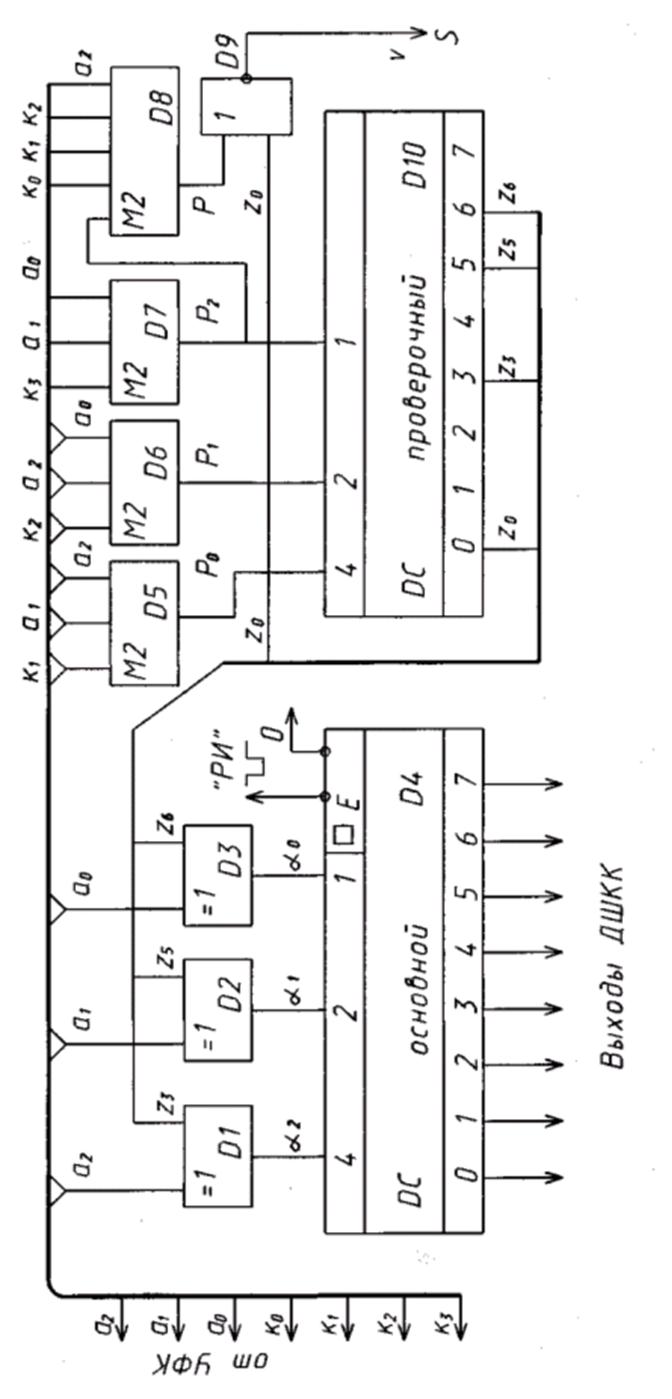
Комбинационный ДШ циклического (7,4) – кода, исправляющий одиночные ошибки, можно построить на основе опознавателей <>, определяемых по выражениям (5):

z3=2p1p0 при ошибке в а0,

z6=p2p10 при ошибке в a1,                      (9)

z4=p2p1p0 при ошибке в а2,

z5=p21p0 при ошибке в а3.

Очевидно, «опознавателем» безошибочного приема кодовой комбинации будет z0=p2p1p0. Если каждому опознавателю (9) поставить в однозначное соответствие двоичное 3-разрядное число, то нетрудно заметить совпадение этих чисел со строчками матрицы дополнений. Отсюда следует простой метод отыскания опознавателей одиночных ошибок: непосредственно из образующей матрицы кода - как логическое произведение элементов матрицы дополнений, соответствующих одной её строке. Например, 4-я строка матрицы С (7,4) имеет вид:

а3   а2   a1   а0   к2   к1   к0

1      0    0     0     1     0     1 →F8(x).

Последовательность элементов <к2к1к0>→101 является строкой матрицы дополнений. Переименовав элементы Kj переменными Pj (j=0,l,2 для данного кода) и заменив нули переменными j, а единицы - Pj (без инверсии), получим

<101>→ p21p0=z5

Единица, стоящая в этой же строке единичной транспонированной матрицы, указывает, что найденное выражение z5 является опознавателем ошибки в элементе <а3>. Аналогично находятся другие опознаватели.

Сравнивая между собой (поэлементно) выражения (9), замечаем, что некоторые из них отличаются только значением одной переменной. Следовательно, возникновение 2-х ошибок может привести к трансформации передаваемого сообщения (d=3; r=s=1).

Процедура исправления ошибок описывается логическими выражениями:

          α0=ā0z3; α1=ā1z6; α2=ā2а4;  α3=ā3z5.            (10)

Целесообразно для реализации зависимостей (10) использовать отдельный ДШ опознавателей, если число проверок k (и контрольных элементов) циклического кода не превышает 5.6. В противном случае (при k>6) наименьшие аппаратные затраты будут, если в качестве ДШ опознавателей применить соответствующим образом запрограммированное ППЗУ в интегральном исполнении.

Методы подготовки данных для программирования ППЗУ на реализацию логических функций с известными алгебраическими выражениями изложены в [3,с.91-93], [4, с. 144-162].

А на рис.7 приведена функциональная схема декодирования циклического (7,4) – кода  с исправлением одиночных ошибок в его информационных элементах. Сравнивая рис. 5-7, нетрудно заметить идентичность и простоту их структур. Конечно, сложность ДШ циклических кодов, исправляющих большее число ошибок (s>1), существенно возрастает из-за усложнения ДШ опознавателей.

Рассмотрим процедуры отыскания данных для построения комбинационного ДШ «усеченного» циклического (15,7)-кода, исправляющего одиночные и двойные ошибки в информационных элементах (d=5,s=r=2). Возьмем псевдоциклический (12,4)-код [1,с.63] с образующей матрицей

a3 a2 a1 a0 k7 k6 k5 k4 k3 k2 k1 k0

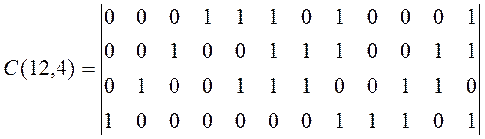                    (11)

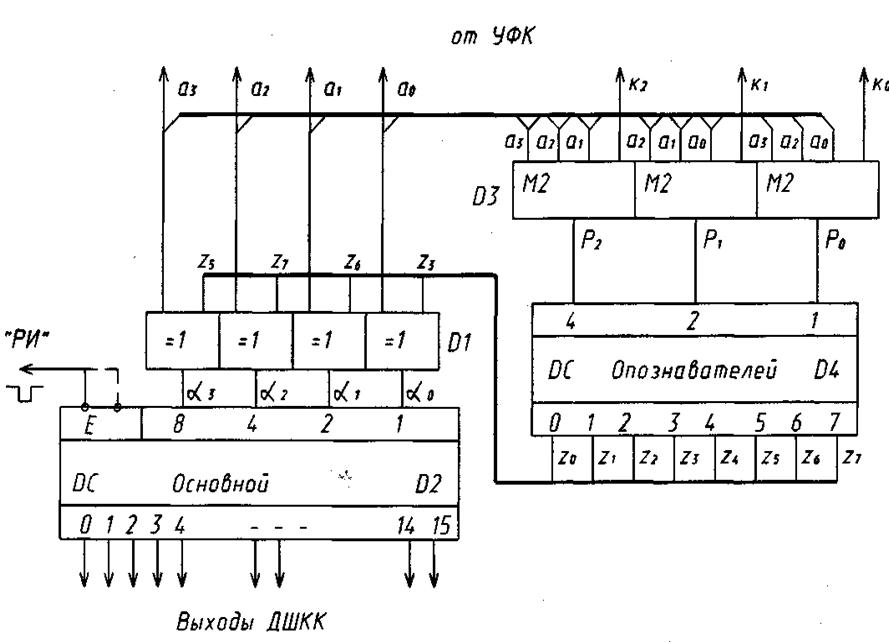
Рис. 7. Комбинационный ДШ циклического (7,4) – кода

Запишем алгебраические выражения проверок на четность, пользуясь (11) и выше изложенной методикой:

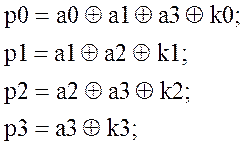
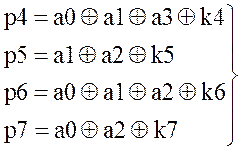                  (12)

Опознаватели будем записывать с индексами информационных элементов, в которых должны исправляться ошибки. Тогда опознаватели одиночных ошибок будут иметь вид:

z0=p7p65p4321p0→1101.0001=D1H,
z1=7p6p5p432p1p0 → 0111.0011=73H,                    (13)

z2=p7p6p543p2p10 → 1110.0110=C6Н,

z3=765p4p3p21p0 → 0001.1101=1DH.

Известно, что опознаватели двойных ошибок находятся как поразрядная сумма по mod 2 опознавателей соответствующих одиночных ошибок. Так как число информационных элементов у данного кода 4, то опознавателей двукратных ошибок будет 6 (С ):