Исследование устойчивости систем с однозначными и неоднозначными нелинейными характеристиками

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

факультет: ИС

кафедра: УИТ

дисциплина: теория автоматического управления

ПОЛОЖЕНИЯ РАВНОВЕСИЯ И УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ

                                                                                            Выполнил ст. гр. УИТ-41

                                                                                            Принял Скоробогатова Т.Н.

Балаково   2007

Вариант №4(25)

Цель работы: исследовать устойчивость систем с однозначными и неоднозначными нелинейными характеристиками, найти и оценить устойчивость имеющихся положений равновесия.

Даны дифференциальные уравнения:

  х₁=-х₁+х₂

  х₂=-х₁-х₂+2х₁х₂+U

Даны значения U=-6, а₀=1.16,  a₁=0.8

Для нахождения положений равновесия необходимо приравнять к нулю производные в дифференциальных уравнениях:

  х₁=0

  х₂=0

  0=-х₁+х₂

  0=-х₁-х₂+2х₁х₂+U

При U=0 имеем:  0=-х₁+х₂

                              0=-х₁-х₂+2х₁х₂ , откуда получим точки (0;0) и (1;1).

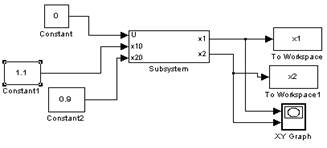
Соберем модель объекта:

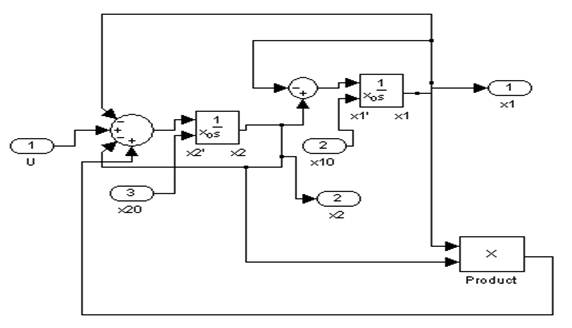
Построим фазовый портрет вблизи точки (0;0):

           

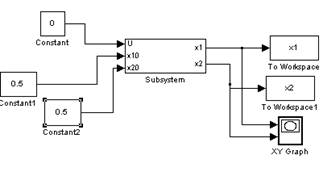
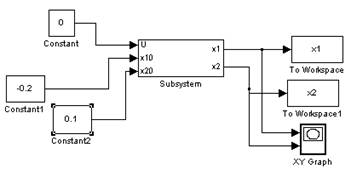
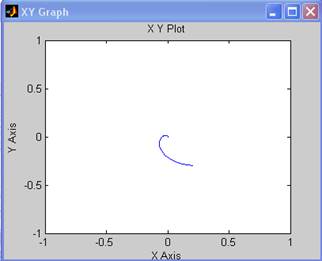
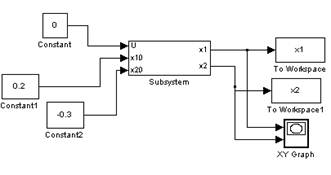
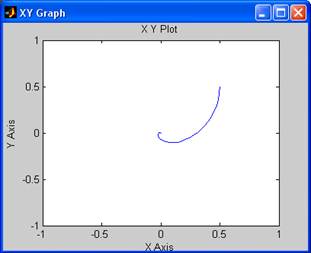
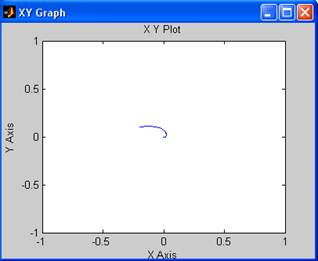
Как видно, графики сходятся при малых отклонениях (0.5;0.5), (-0.2,0.1), (0.2,-0.3) в точку (0,0), следовательно, точка (0,0) является устойчивой.

Построим фазовый портрет вблизи (1;1):

        

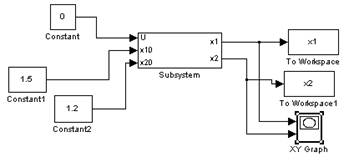
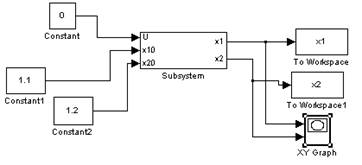
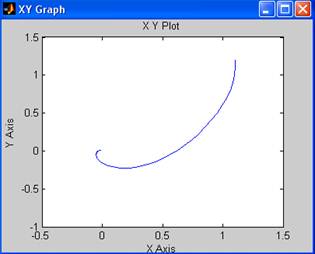
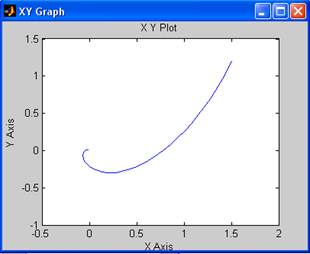
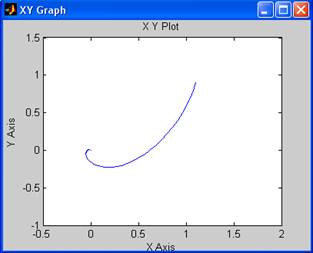
При заданных малых отклонениях (1.1;1.2), (1.5,1.2), (1.1,0.9) фазовые траектории расходятся от положения равновесия, следовательно, точка (1;1) является неустойчивой.

При U=-6 имеем:   0=-х₁+х₂

                                 0=-х₁-х₂+2х₁х₂-6 , откуда получим точки (2.3;2.3) и (-1.3;-1.3).

Построим фазовый портрет вблизи точки (2.3;2.3):

          

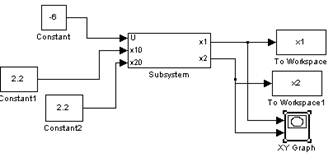
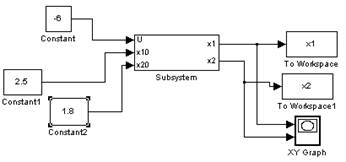
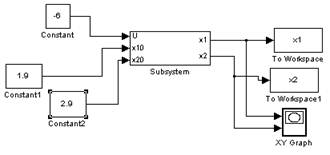
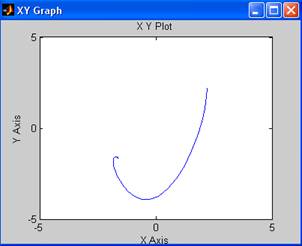
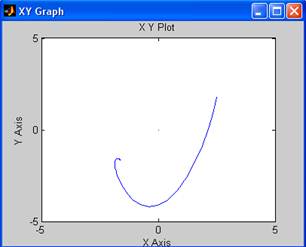
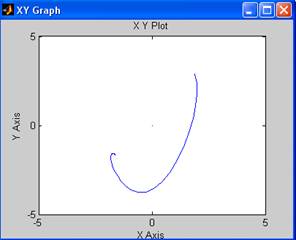
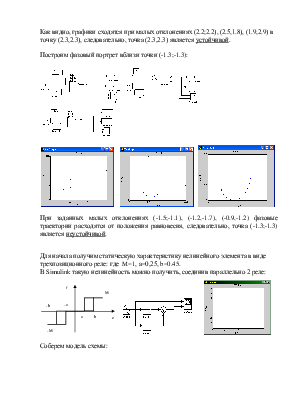
Как видно, графики сходятся при малых отклонениях (2.2;2.2), (2.5,1.8), (1.9,2.9) в точку (2.3,2.3), следовательно, точка (2.3,2.3) является устойчивой.

Построим фазовый портрет вблизи точки (-1.3;-1.3):

     

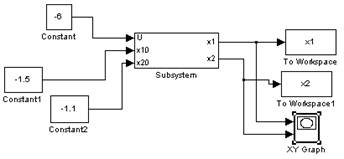
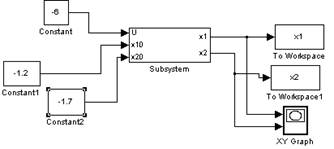
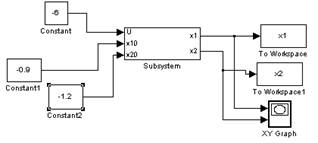
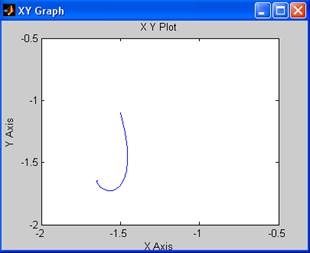
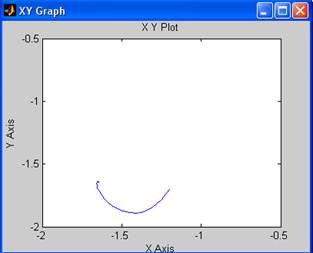
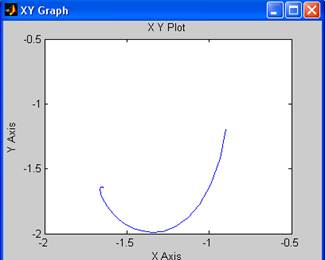
При заданных малых отклонениях (-1.5;-1.1), (-1.2,-1.7), (-0.9,-1.2) фазовые траектории расходятся от положения равновесия, следовательно, точка (-1.3;-1.3) является неустойчивой.

Для начала получим статическую характеристику нелинейного элемента в виде трехпозиционного реле: где  M=1, а=0,25, b=0.45.

В Simulink такую нелинейность можно получить, соединив параллельно 2 реле:

     

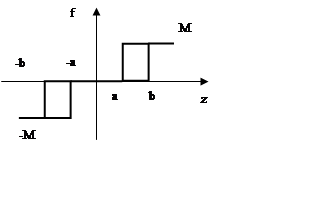
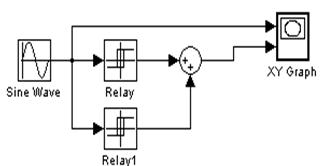
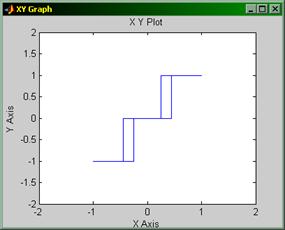
Соберем модель схемы:

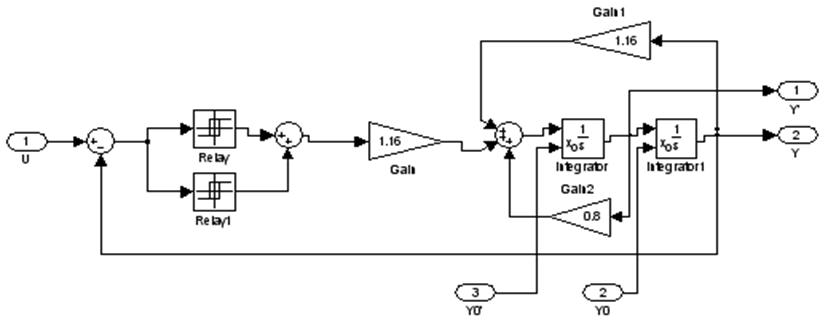
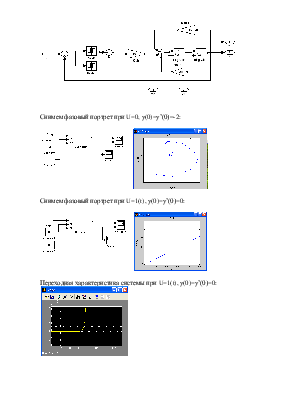
Снимем фазовый портрет при U=0, y(0)=y’(0)=-2:

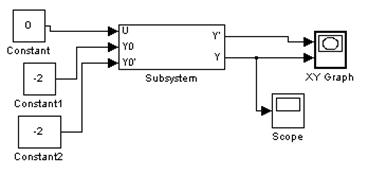
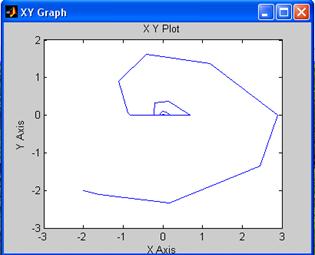
Снимем фазовый портрет при U=1(t), y(0)=y’(0)=0:

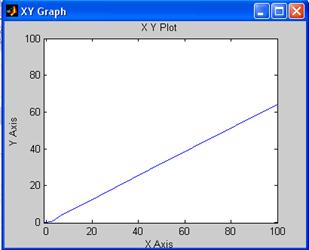
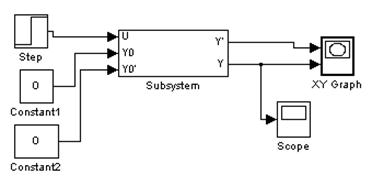
Переходная характеристика системы при U=1(t), y(0)=y’(0)=0:

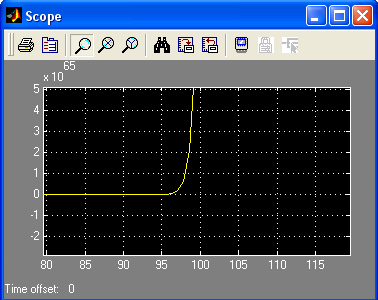
По данным графикам фазового портрета и переходной функции получили, что система с нелинейным элементом трехпозиционным реле не устойчива.

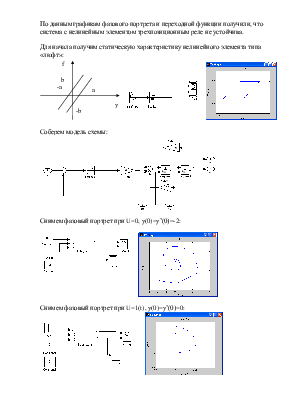
Для начала получим статическую характеристику нелинейного элемента типа «люфт»:

  

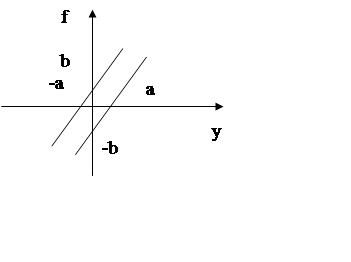
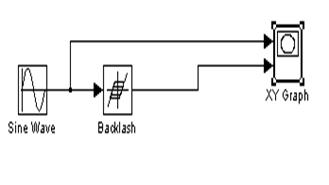
Соберем модель схемы:

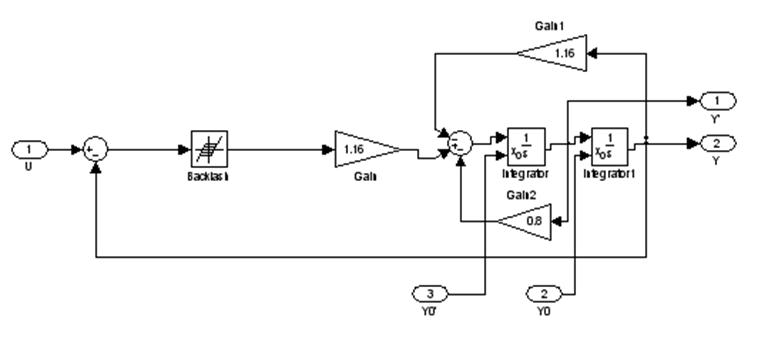
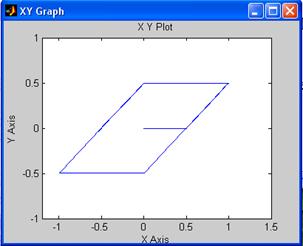
Снимем фазовый портрет при U=0, y(0)=y’(0)=-2:

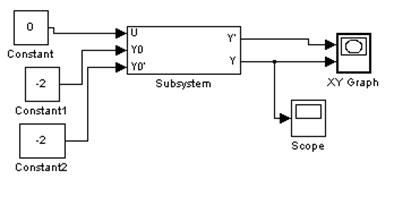
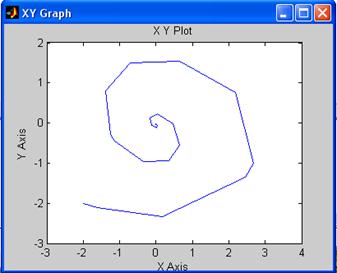
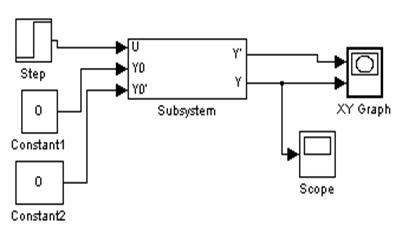
Снимем фазовый портрет при U=1(t), y(0)=y’(0)=0:

    

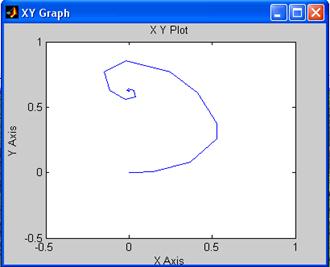
Переходная характеристика системы при U=1(t), y(0)=y’(0)=0:

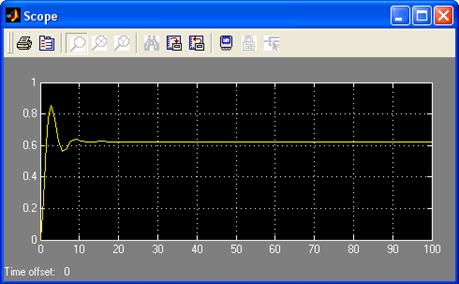
По данным графикам фазового портрета и переходной функции получили, что система с нелинейным элементом типа «люфт» устойчива.