Исследование устойчивости линейных и нелинейных систем автоматического управления, страница 2

 

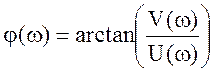
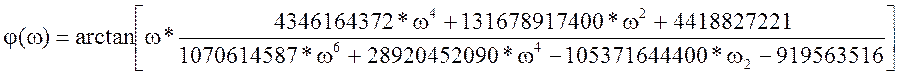
Рисунок 9

4.3 Построение АФЧХ, ЛАЧХ и ЛФЧХ системы

Построение АФЧХ заключается в отображении на координатных осях U(ω) и  V(ω).

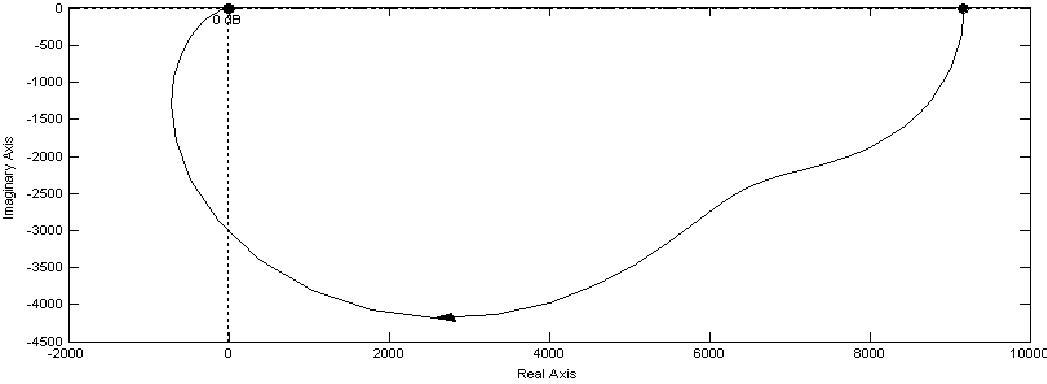
Рисунок 10

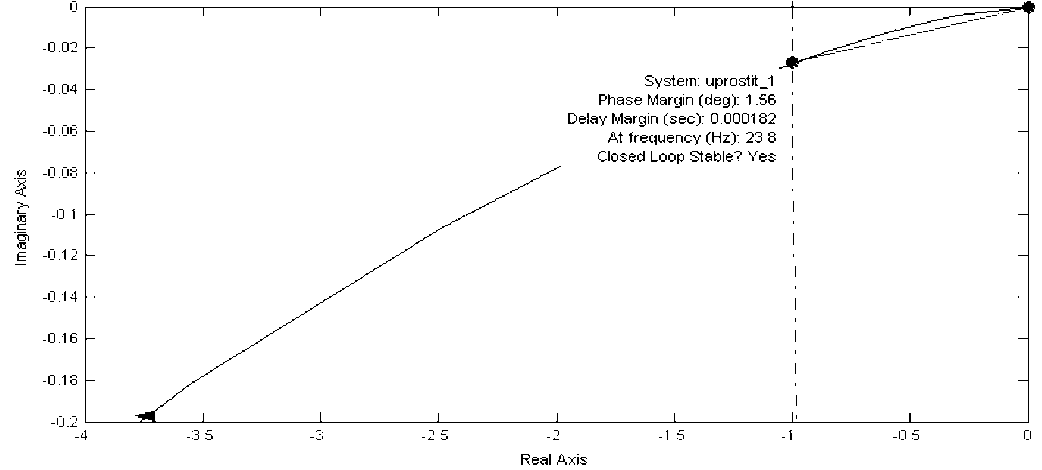Актуализируем участок (-1;0)

Рисунок 11

Совместное построение ЛАЧХ и ЛФЧХ

Логарифмические характеристики строятся с использование следующих формул:

Логарифмическая АЧХ:

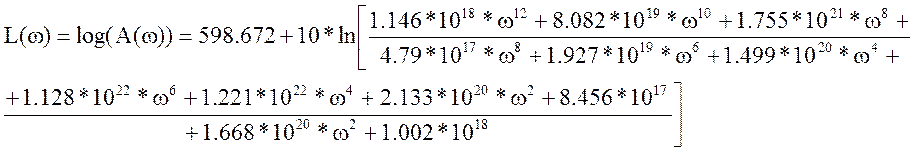
ЛФЧХ есть ФЧХ рассматриваемая как функция ln(ω)

 

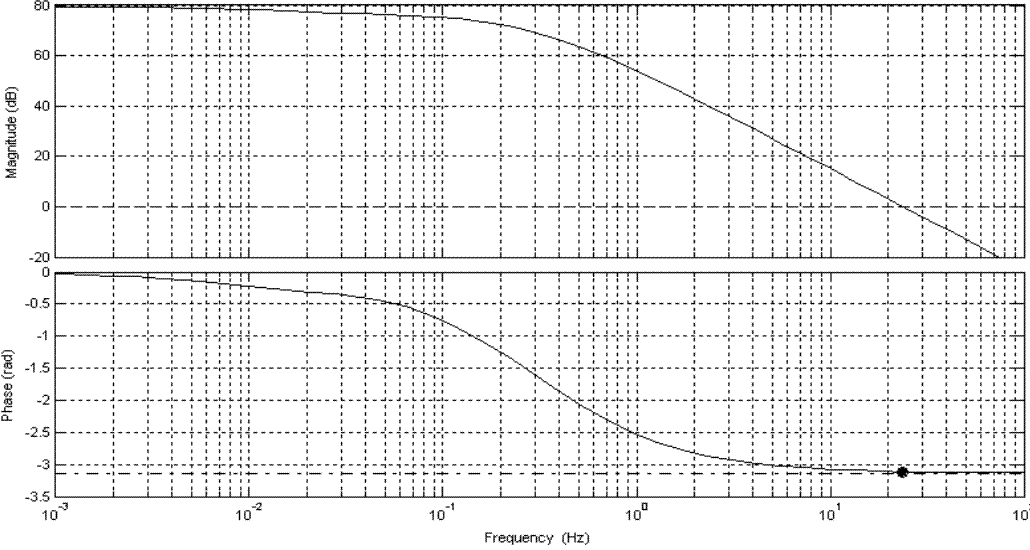Рисунок 12

Суммируя данные из рисунков 11 и 12, определим:

запас устойчивости по фазе составляет γ_С=1.56⁰

запас устойчивости по амплитуде L_ЗАП=73.9 дБ

4.4 Построение графика переходного процесса

Переходный процесс в системе, это реакция на единичное ступенчатое воздействие

Передаточная функция системы записывается как:

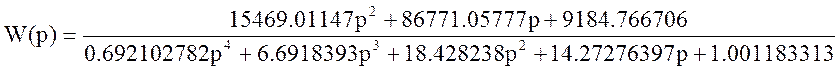
Тогда переходная функция примет вид:

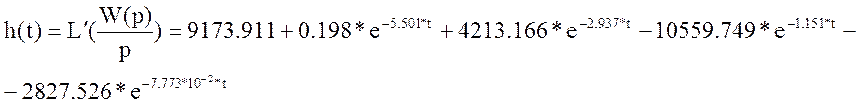
По данной переходной функции построим переходную характеристику.

 

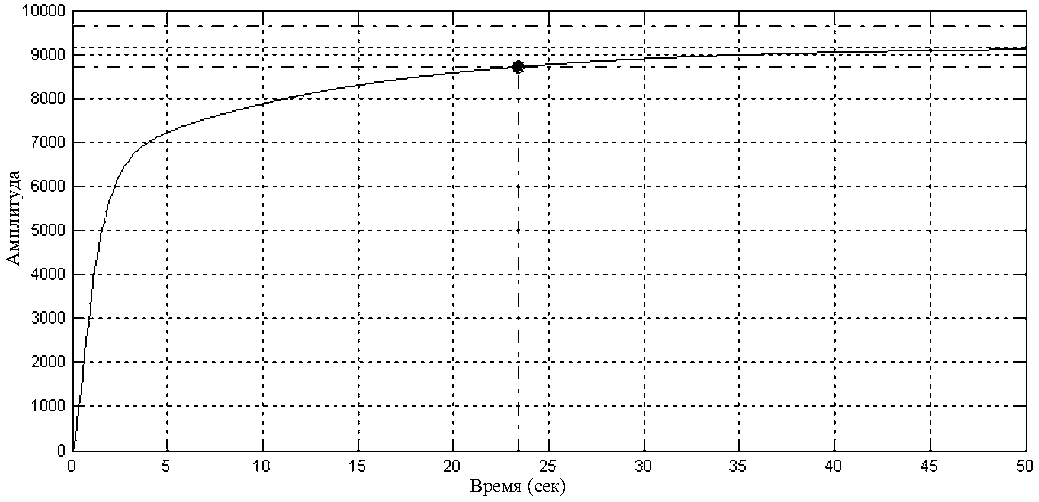Рисунок 13

5 Анализ качества управления

Используя рисунок 13, определим следующие величины:

1) Установившееся значение h_УСТ=

2) Время переходного процесса t_П=23.4 c

3) Перерегулирование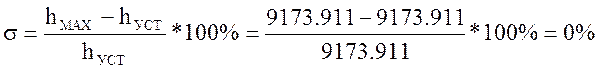

4) Период колебаний Т=∞

5) Частота колебаний ω=0

6) Колебательность n=0

7) Время нарастания регулируемой величины t_Н=∞

8) Время первого согласования t_ПС=∞

Используя график 1, определим следующие величины:

1) Резонансная частота ω_Р=2.47*10^-11

2) Показатель колебательности M=A_MAX/A₀=1

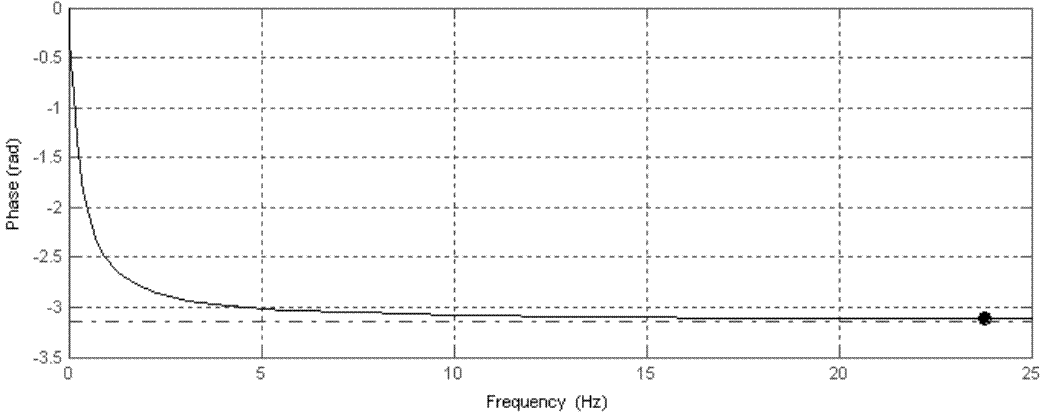
3) Частота среза ω_СР=23.96 Гц

ВЫВОД

Проведя ряд упрощений исходной передаточной функции, был получен ряд значений характеризующих систему. Анализ значений показывает, что система весьма точна в регулировании и не имеет колебаний. Однако другие характеристики говорят о низком запасе устойчивости по фазе, что весьма неблагоприятно скажется на управлении системы при изменении некоторых параметров управления. Данную ситуацию простым изменением коэффициентов исправить не удалось, есть вероятность, что требуется ввод дополнительных звеньев. Достаточно большой запас устойчивости по амплитуде дает шанс серьезного изменения коэффициентов усиления основной цепи, без потери устойчивости.

ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ САУ

1 Техническое задание

Рисунок нелинейной САУ приведена на рисунке 14.

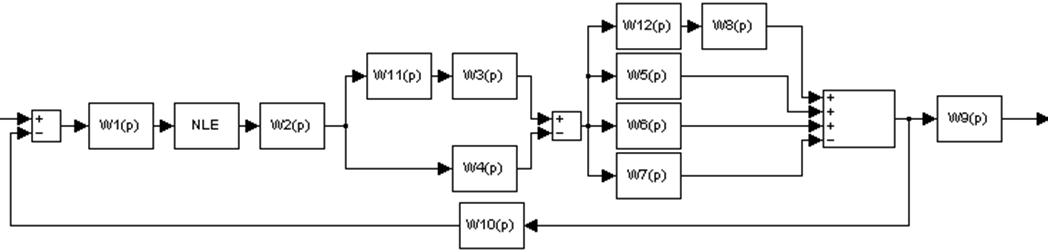
Рисунок 14

Где: W₁(p)=38; W₂(p)=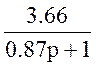; W₃(p)=0.74; W₄(p)=0.74; W₅(p)=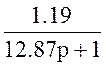; W₆(p)=;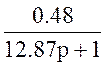

W₇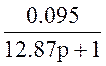(p)=; W₈(p)=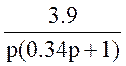; W₉(p)=16.3; W₁₀(p)=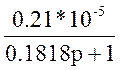; W₁₁(p)=2; W₁₂(p)=p.

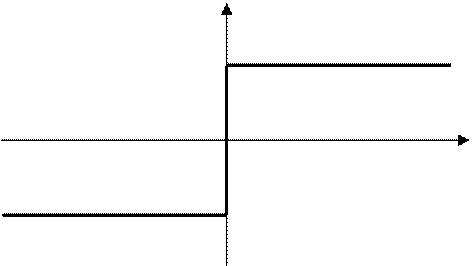
График, описывающий нелинейный элемент NLE приведен на рис. 15

                                                                      y        

                                                                     10

    0

                                                                                                           x

                                                                            -10

Рисунок 15

2 Упрощение структурной схемы САУ

Выделим линейный и нелинейный элемент, приведем систему к следующему виду:

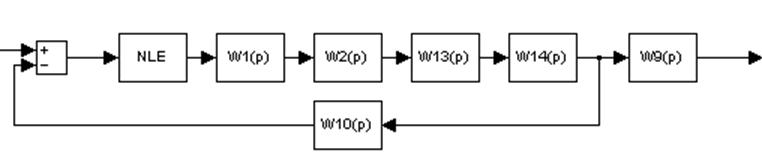
Рисунок 16

Обозначение: W₁₃(p)=W₁₁(p)*W₃(p)-W₄(p); W₁₄(p)=W₁₂(p)*W₈(p)+W₅(p)+W₆(p)-W₇(p)

Продолжим упрощение, разделяя линейную и нелинейную части.

 

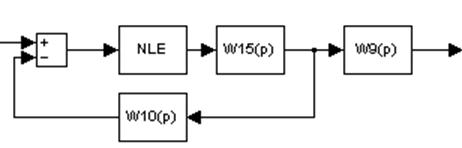
Рисунок 17

Обозначение: W₁₅(p)=W₁(p)*W₂(p)*W₁₃(p)*W₁₄(p)

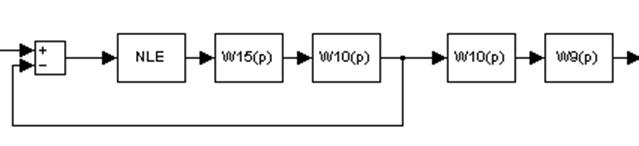Приведем эту систему к виду:

Рисунок 18

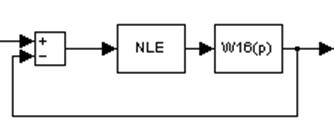Сгруппируем звенья:

	u		u-x		x1		x

 

Рисунок 19

Обозначение: W₁₆(p)=W₁₅(p)*W₁₀(p)=W₁(p)*W₂(p)*(W₁₁(p)*W₃(p)-W₄(p))*

*( W₁₂(p)*W₈(p)+W₅(p)+W₆(p)-W₇(p))*W₁₀(p)

Передаточная функция линейной части запишется в виде

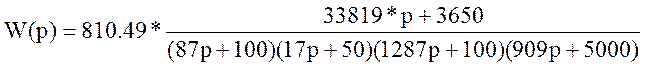
3 Построение фазового портрета

Передаточная функция есть 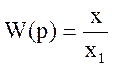 или . Получим:

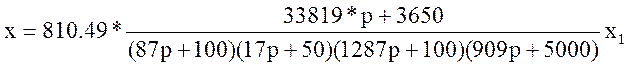
Приведем к виду:

 ()*x= (27409961.31*p+2958288.50)*x₁

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.

Введем замену pⁱx=y_i и исключим из правой части уравнения производную

Получим систему уравнений:

Для участка [-∞;0] и [0;+∞]:

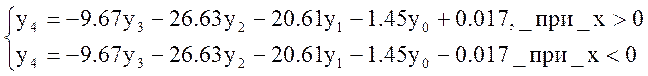
Создадим матрицу для решения дифференциального уравнения:

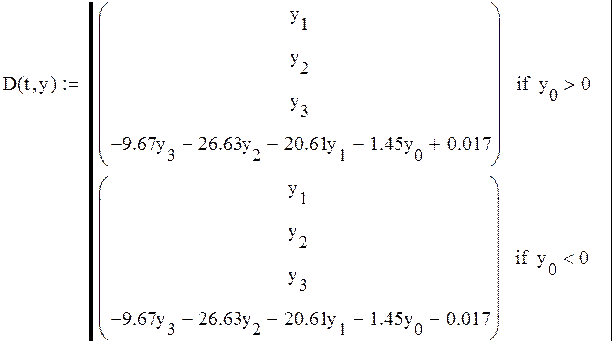
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицу начальных условий:

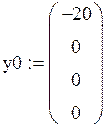
Возьмем количество точек равным 1000 и конечное время интегрирования 100, то матрица решений запишется как: .

По введенным данным получим фазовый портрет (рисунок 20).

Рисунок 20

Вывод: на рисунке 20 представлен фазовый портрет нелинейной системы. Это типовой вид кривой. До перехода через точку 0 работает первое уравнение системы, при переходе через эту точку начинает работать второе уравнение. Характер фазовой линии такой, что она постоянно приближается к началу координат, т.е. нелинейная система с релейным элементом устойчива. При движении к состоянию устойчивости амплитуда колебаний постоянно уменьшается, а частота переключения растет. Получаем, что амплитуда колебаний в итоге примет нулевое значение, а частота колебаний станет бесконечно большой.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1 Основы автоматического регулирования/Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.

2 Теория автоматического управления/Под ред. А. В. Нетушила.– М.: Высшая школа, 1976. – 400 с.: ил.

3 Основы теории автоматического регулирования/А.А. Воронов и др. – М.: Высшая школа, 1977. – 519 с.: ил.

4 Автоматические приборы и регуляторы/ Кошарский Б.Д., Бек В.А., и др. – М.: Машиностроение, 1964. – 704 с.: ил.

5 Автоматизация производства и промышленная электроника/Берг А.И., Трапезников В.А. – М.: Советская энциклопедия, 1962. –  544 с.: ил.