Математическое описание линейных систем, страница 2

Нормальная форма уравнений состояния имеет вид:

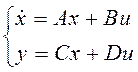                                                 (1.2)

Здесь А – квадратная матрица определенного вида, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы, элементы нижней строки – коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком. Все остальные элементы – нули. Такая матрица называется матрицей Фробениуса.

Согласно (4.1) дифференциальное уравнение системы имеет вид:

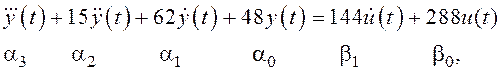
где   и – коэффициенты уравнения.

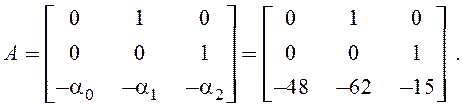
Элементы матриц B и D вычисляются по следующим рекуррентным соотношениям: 

,     ,      

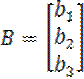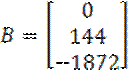Подставив рассчитанные матрицы в систему (4.2), получим

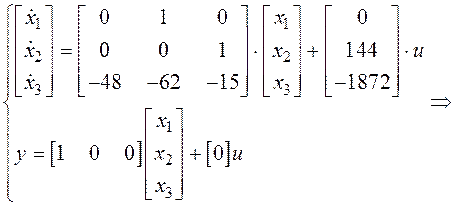
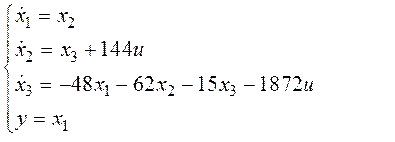
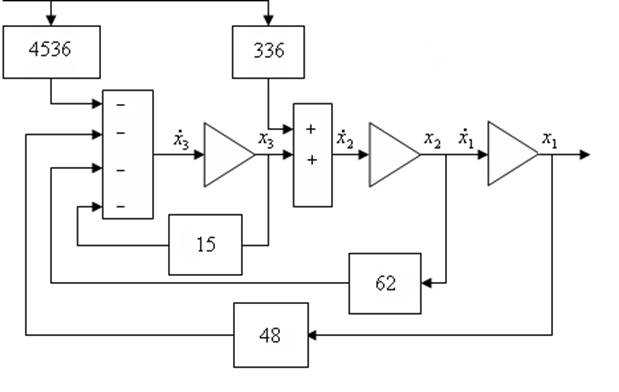
Схема модели приведена на рис. 4.6.

∫

∫

∫

144

1872

144

1872

Рис. 1.6

Записать уравнения состояния в канонической форме. Изобразить схему моделирования.

Введем новую переменную состояния q, которая связана с переменной состояния x следующим образом: х = М q. М – это модальная матрица, которая имеет вид

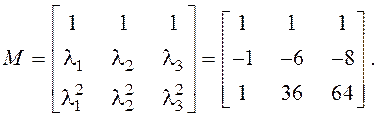
где l_i – характеристические числа матрицы Фробениуса А.

При подстановке q вместо x в нормальную форму уравнений состояния (1.2), то после преобразований получим уравнения состояния системы в канонической форме:

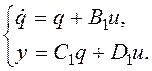                                              (1.3)

Здесь L – диагональная матрица:

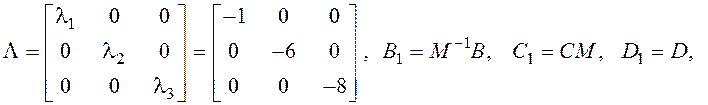
где M^-1 – матрица, обратная модальной.

,

где  AdjM – матрица, присоединённая к M, т. е. транспонированная матрица алгебраических дополнений.

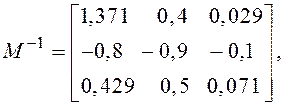
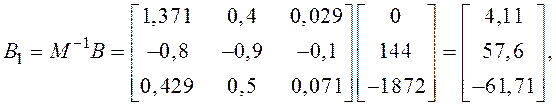
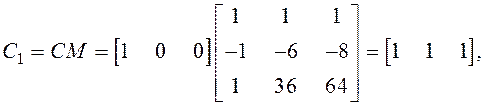
Matlab

>> M=[1 1 1;-1 -6 -8; 1 36 64]

M =

1     1     1

-1    -6    -8

1    36    64

inv(M)

ans =

1.3714    0.4000    0.0286

-0.8000   -0.9000   -0.1000

0.4286    0.5000    0.0714

B=[0;144;-1872]

B =

0

144

-1872

M^-1*B

ans =

4.1143

57.6000

-61.7143

Подставив найденные значения в (1.3), получим

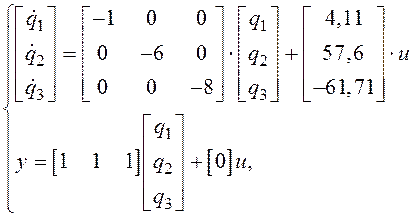
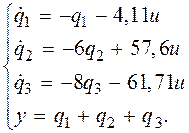
Схема модели, соответствующая полученной системе, приведена на рис. 4.7. Для нее характерно параллельное соединение интеграторов, выходы которых определяются переменными состояния q₁, q₂, q₃.

Блок-схема модели

 

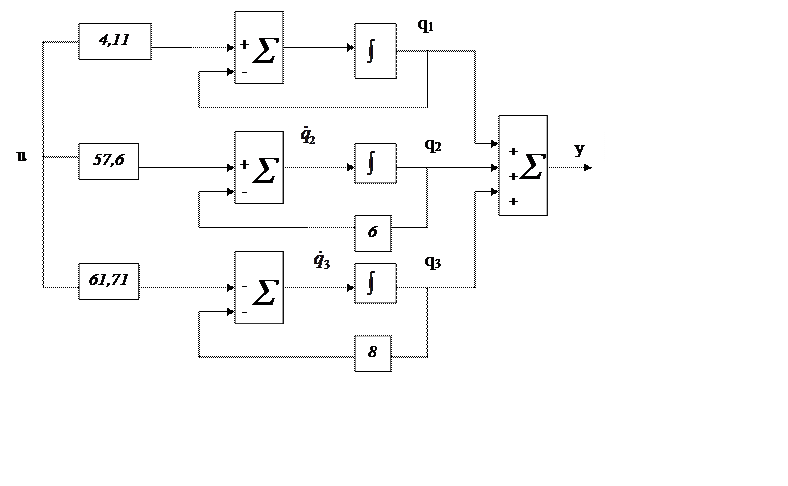
Рис. 1.7

Найдем решение y(t) для системы уравнений в нормальной форме, если начальные условия имеют вид:  Сигнал  Переходя к начальным условиям для х, в соответствии с принятыми ранее обозначениями получим  

Решение уравнения состояния  складывается из двух составляющих  – свободной и вынужденной.

Свободная составляющая –  это общее решение дифференциального уравнения системы с нулевой правой частью. Оно не зависит от внешнего воздействия и характеризует естественное поведение системы.

Вынужденная составляющая – это частное решение дифференциального уравнения с ненулевой правой частью. Оно зависит от сигнала  и характеризует поведение системы под его воздействием.

Решение уравнения состояния имеет вид

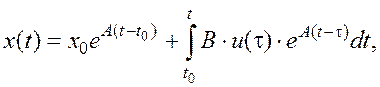
где  – фундаментальная матрица или матрица перехода.

Она вычисляется по следующей формуле:

где  – неизвестные коэффициенты.

Вычислить их можно, решая матричное уравнение

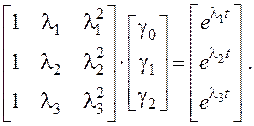
Для рассматриваемого примера

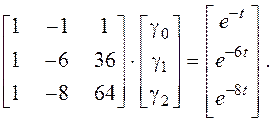
Перемножая матрицы, получаем систему уравнений следующего вида

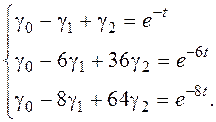
Решение данной системы уравнений имеет вид

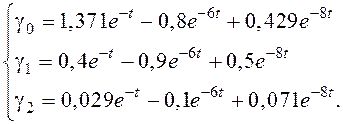
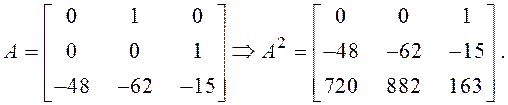
Итак,

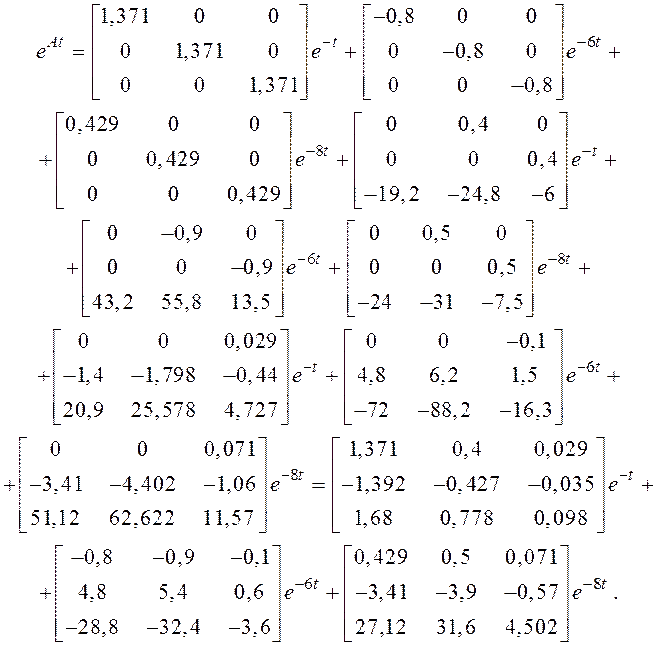
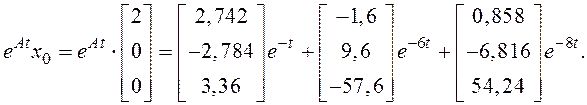
Так как , то свободная составляющая выходного сигнала будет равна  Определим вынужденную составляющую при входном сигнале u(t) = 2*1(t). Сигнал на выходе при поступлении на вход 1(t) уже вычислен – это переходная характеристика системы (1.4). Чтобы получить вынужденную составляющую сигнала в нашем случае  – умножим переходную характеристику на 2.

Таким образом, сигнал на выходе системы будет следующим:

     

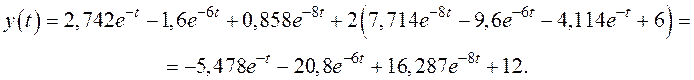
Выполним проверку:

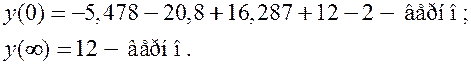
Найдем решение уравнений состояния, представленных в канонической форме (4.3). Каждое из дифференциальных уравнений первого порядка  зависит только от одной переменной и его решение в общем виде имеет вид

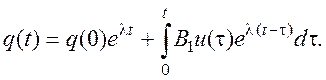
Определим начальные условия  для вектора

Так как  , то

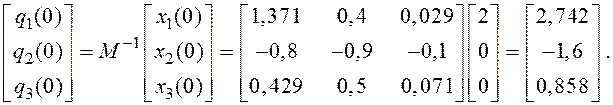
Найдем выражения для  и

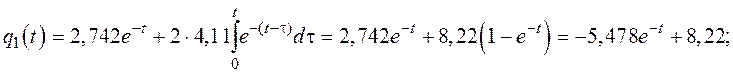
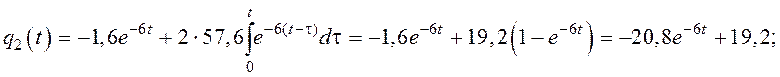
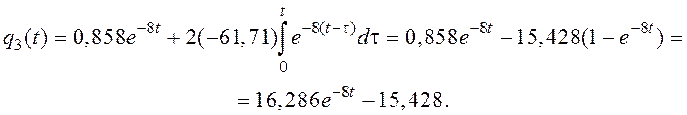
В результате получим

Выполним проверку:

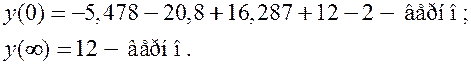
Решения нормальных и канонических уравнений состояния совпадают.

Проверим, одинаково ли значение коэффициента усиления: по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики.

Проверим значение коэффициента усиления по передаточной функции

По переходной характеристике:

По моделям в пространстве состояний.

Каноническая форма:

Нормальная форма (в установившемся режиме на входах интеграторов нули): 

По аналитической записи импульсной переходной характеристики:

Мы видим, что значение коэффициента усиления одинаково.