Математическое моделирование и исследование с разработкой программных продуктов, страница 3

Компетенция определяется как:

1.  Способность делать что-либо хорошо или эффективно.

2.  Соответствие требованиям, предъявляемым при устройстве на работу.

3.  Способность выполнять особые трудовые функции.

По В. Д. Шадрикову, «компетенция является системным проявлением знаний, умений, способностей, и личностных качеств. В каждой деятельности вес этих компонентов и их сочетания могут существенно различаться. В образовательном процессе наблюдается определенная диалектика в формировании компетенций. Компетенции формируются на основе знаний, умений, способностей, личностных качеств, но сами эти знания и др. во многом не являются компетенциями, они выступают как условия для формирования компетенций. Было бы большой ошибкой (которая намечается), если при реализации компетентностного подхода мы противопоставим его знаниям, умениям, способностям, личностным качествам».

4.  Краткое описание используемого математического аппарата

Упростим общую математическую модель, предполагая, что моделируется развитие личности на ограниченном временном промежутке – а именно, в течение семестра. За такой период квалификация изменится сравнительно незначительно, что позволяет принять значения квалификации  в правых частях дифференциальных уравнений постоянными и равными начальным  (или некоторым средним, близким к начальным) ее значениям.

Введем переменные

,

.

В течение семестра выполняется одна исследовательская работа, таким образом, ее структура, то есть соотношение различных компонентов исследовательской деятельности, остается постоянным, то есть эти переменные также являются константами

Тогда уравнение мотивации принимает вид

.

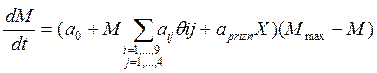Приведем это уравнение к безразмерному виду, введя переменные

.

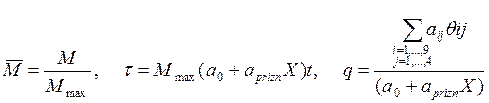Тогда при  уравнение получит вид:

.

Легко показать, что общее решение этого уравнения имеет вид

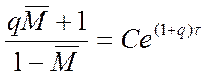
или

.

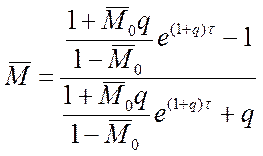Легко проверить, что

.

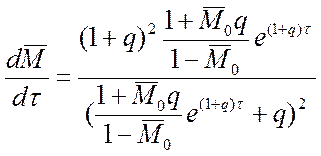Таким образом, знак этой производной определяется знаком выражения . При  мотивация будет монотонно убывать, при  - возрастать, при  - оставаться неизменной.

Учитывая, что в правых частях дифференциальных уравнений квалификация приближенно принята постоянной, можно записать выражение для приращения общей квалификации за семестр

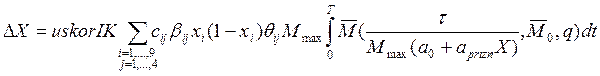
или

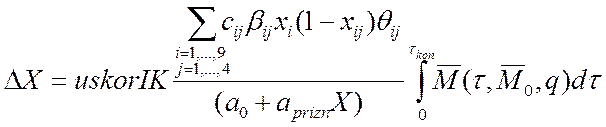, где .

Опуская положительный сомножитель, получим следующую оптимизационную задачу для определения оптимальной структуры исследовательской работы в течение семестра:

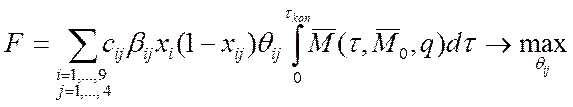
при условиях

.

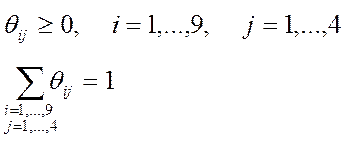К ее ограничениям можно добавить дополнительные условия, накладываемые на структуру исследовательской работы . Заметим, что они будут носить линейный характер относительно этих переменных.

Итак, получилась существенно нелинейная задача оптимизации функции 36 переменных. Можно предложить следующий эффективный метод ее решения. Предположим, что мы зафиксировали значение . Тогда оптимизационная задача сведется к следующей:

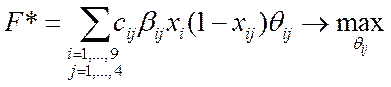
при условиях

.

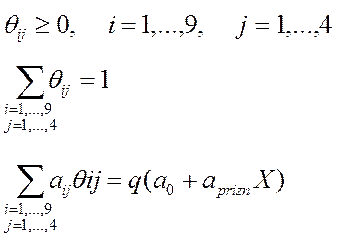Это достаточно простая задача линейного программирования, которая сравнительно легко может быть решена. Полученное оптимальное значение критерия  будет, наряду с известными исходными данными, зависеть от величины , то есть . Тогда исходную оптимизационную задачу можно записать как задачу оптимизации функции одной переменной :

.

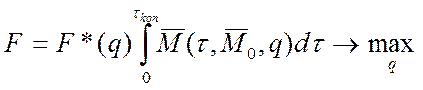Эта задача легко решается численно.

5.  Исходные данные

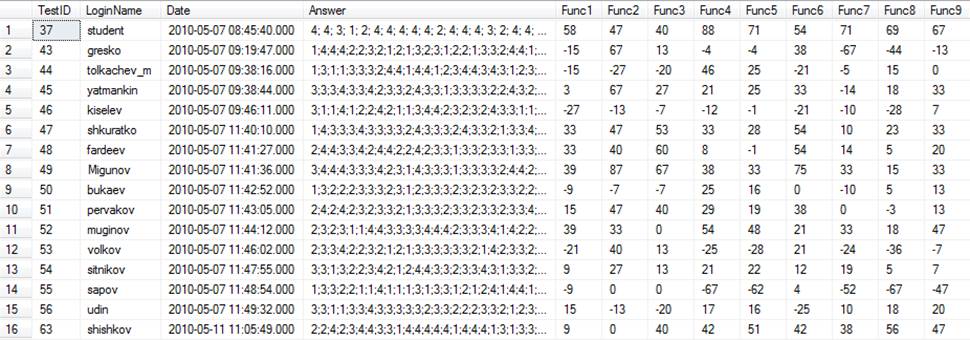
Для получения исходных данных был рассмотрена система индивидуального руководства исследованиями студентов на ФИСТ СГАСУ. Данные брались из имеющейся в этой системе базы данных. А в частности результаты тестов «Квалификации» и «Деятельности-Мотивации».

рис.1 – результаты теста «Деятельность-Мотивация»