Математика \ Математика

Розв’язок методом алгоритму RADAUS. Реалізація перетворення Лапласа засобами MathCAD, страница 2

Для вирішення проблем, пов'язаних з системою рівнянь, Булирш і Штерн узагальнили алгоритм Невілля на випадок раціональної інтерполяції. Алгоритм Булирша – Штерна отримує раціональну функцію зі ступенями чисельника і знаменника, рівними N/2. Недолік методу в тому, що не для кожного набору точок можливо побудувати інтерполянт такого виду, причому алгоритм не передбачає виявлення подібних помилок. Тим не менше, довгий час цей алгоритм залишався єдиним доступним способом раціональної інтерполяції.

Підготовка для застосування вбудованих інтеграторів MathCAD (rkfixed, Булирша-Штерна тощо) вимагає попереднього формування функції f(t,x), де x – вектор, що складається з імен шуканих функцій.

Алгоритм Булирша – Штерна знайшов своє застосування у MathCAD у вигляді функції bulstoer. Використання функції bulstoer, як і інших перелічених вище функцій, виглядає наступним чином: bulstoer(y,a,b,acc,D,kmax,s).

Розв’язок методом Булирша-Штерна

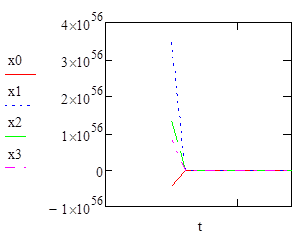
Реалізація перетворення Лапласа засобами MathCAD

У середовищі MathCAD знайти Лаплас-зображення заданої функції можна двома шляхами:

а) через команди командного меню Symbolics|Transform|Laplace;

б) через меню панелі символьного редактора. При цьому випадку аргумент функції-зображення має бути вказаним після звернення до ключового слова laplace.

Зворотнє перетворення Лапласа здійснюється шляхом застосування команд Symbolics|Transform|InverseLaplace або через ключове слово invlaplace палітри символьного редактора. В останньому випадку після ключового слова вказується ім’я аргумента функції-оригінала. Приклад здійснення вказаних операцій наведено на рис.

Одержання зображення функції

f(t) = t^1/2:

Зворотна трансформація зображення:

Розв’язок методом Лапласа

Метод Рунге-Кутта

Методи Рунге — Кутта — важлива група чисельних методів розв’язування (систем) звичайних диференціальних рівнянь. Названі на честь німецьких математиків Карла Рунге і Мартіна Кутта, які відкрили ці методи.

Метод Рунге — Кутта 4-го порядку настільки широко розповсюджений, що його часто називають просто методом Рунге — Кутта.

Розглянемо задачу Коші для системи диференціальних рівнянь довільного порядку, що записується у векторній формі як

$\textbf{y}'=\textbf{f}(x,\textbf{y}),~~~~~ \textbf{y}(x_0)=\textbf{y}_0$ .

Тоді значення невідомої функції в точці $\ x_{n+1}$ обчислюється відносно значення в попередній точці $\ x_n$ по такій формулі:

$\textbf{y}_{n+1} = \textbf{y}_n + {h \over 6} (\textbf{k}_1 + 2\textbf{k}_2 + 2\textbf{k}_3 + \textbf{k}_4)$ ,

$\ x_{n+1}=x_n+h$

де $\ h$ — крок інтегрування, а коефіцієнти $\textbf{k}_n$ розраховуються таким чином:

$\textbf{k}_1 = \textbf{f} \left( x_n, \textbf{y}_n \right),$

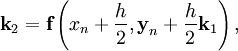
$\textbf{k}_2 = \textbf{f} \left( x_n + {h \over 2}, \textbf{y}_n + {h \over 2} \textbf{k}_1 \right),$

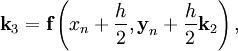
$\textbf{k}_3 = \textbf{f} \left( x_n + {h \over 2}, \textbf{y}_n + {h \over 2} \textbf{k}_2 \right),$

$\textbf{k}_4 = \textbf{f} \left( x_n + h, \textbf{y}_n + h\textbf{k}_3 \right).$

Це метод 4-го порядку, тобто похибка на кожному кроці становить $\ O(h^5)$ , а сумарна похибка на кінцевому інтервалі інтегрування є величиною $\ O(h^4)$ .

1 2 3

Скачать файл

Розв’язок методом алгоритму RADAUS. Реалізація перетворення Лапласа засобами MathCAD, страница 2

Одержання зображення функції

f(t) = t1/2:

f(t) = t^1/2: