Дискретные функции - функции, заданные только в некоторых точках оси

Дискретные функции

Функции, заданные только в некоторых точках оси t (называются дискретными. Будем рассматривать функции, которые определены в равноотстоящих точках оси времени . Здесь k – любое целое число, T – постоянная, которая называется периодом дискретности.

Дискретная функция обозначается - , где  - аргумент дискретной функции.

Любой непрерывной функции x(t) можно подставить в соответствие множество дискретных функций, если представить аргумент t в следующем виде . Где .

При каждом фиксированном значении , функцию можно представить как решетчатую функцию в точках . Это иллюстрирует рисунок 1:

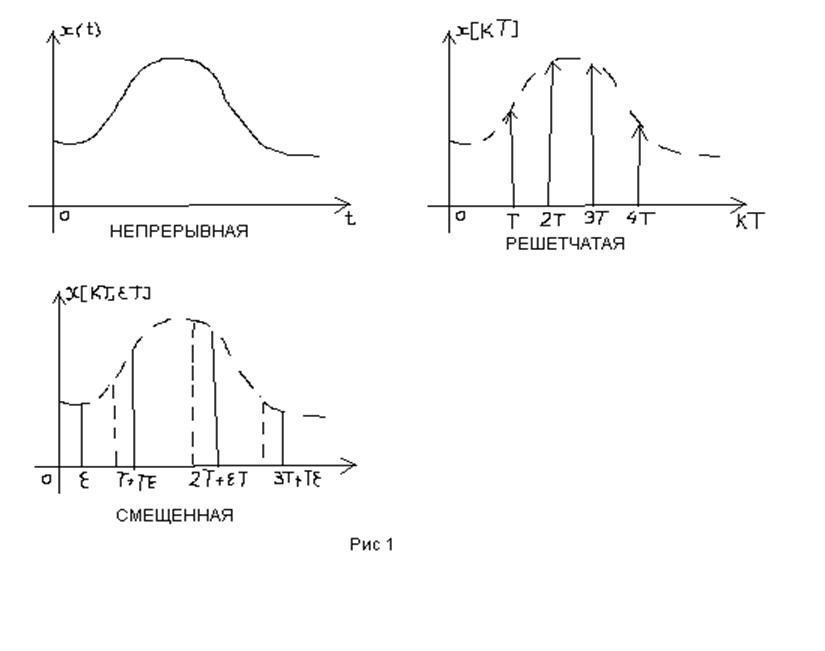
Такие функции называются смещёнными дискретными функциями и обозначаются следующим образом - . Если изменять  от 0 до 1, то можно получить множество дискретных функций, которые соответствуют заданной непрерывной функции. Благодаря непрерывной функции x(t), функция  является также непрерывной функцией относительно параметра .

Функция  является функцией одного аргумента k при фиксированном значении Т. Поэтому в дальнейшем параметр Т будем опускать и писать функцию в виде . Также и смещённая функция  зависит от параметров k и . Обозначим ее .

Операции над дискретными функциями.

1) Конечные разности дискретных функций.

Выражение вида:

   (1)

Называется конечной разностью первого порядка, то есть  - первая разность функции .

Первая разность от дискретной функции  называется разностью второго порядка:

     (2)

И аналогично для n-ого порядка получим разность n-ого порядка:

    (3)

Любую разность функции  можно выразить через значения функции. Разность второго порядка:

Разность третьего порядка:

Разность n-го порядка:

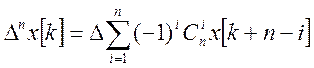
Взятие разности является линейной операцией, т.е. справедливо отношение:

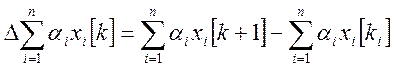
Где - постоянное число.

2) Суммирование дискретных функций.

Пусть задана дискретная функция  при k=0,1,… Требуется найти функцию , которая является первой разностью для функции .

Эта функция имеет вид:

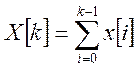
Если рассмотреть первую разность от этой функции, то получим:

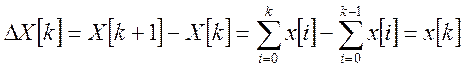
Итак называется первообразной от . Если теперь функция  определена при любом целом значении k, то для определения первообразной надо потребовать, чтобы при любом конечном значении k, ряд 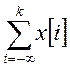 сходился. В этом случае первообразная будет определена следующим выражением:

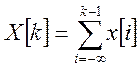
Если теперь  является первообразной для , то функция , где C –постоянное число, также является первообразной:

Таким образом общий вид первообразной от функции  является:

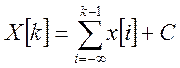
Значение постоянной С можно выразить через значения первообразной при некотором фиксированном значении аргумента, например, k=N.

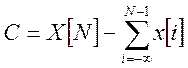
И первообразная:

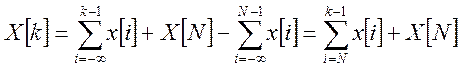
После преобразования последней формулы получим значение первообразной для любого k>N:

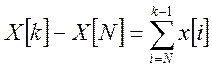  (4)