:Штурм-Луивилдің болымсыз операторы, страница 9

МӘСЕЛЕНІҢ МӘНІ.  Гильберттің кеңістігінде Штурм-Лиувиллдің болымсыз есебіне сәйкес келетін Штурм-Лиувилл операторының спектрәлдік қасиетін зерттеу керек.

ЛЕММА 1.3. Егер а)       ,

б)      , то  и  или болса, онда  ,  немесе    

мұндағы - комплекс сан.

ДӘЛЕЛІ.

,  .

Бұл сәтте келесі жағдайлардың бірі орындалады

1) , онда , мұнан  и .

2) , демек, . Онда   болсын делік , .

3) , бұл жағдай 2)жағдай сияқты

2.2. Штурм-Лиувиллдің болымсыз есебінің шекаралық шартын қорытып шығару

 кеңістігінде  Штурм-Лиувиллдің болымсыз шекаралық есебін қарастырайық

,                                                                (2.1)

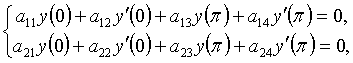                             (2.2)

мұндағы - комплекс мәнді үздіксіз функция, ал - комплекс сан ,

,                                                     (2.3)

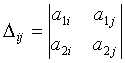,  .                                              (2.4)

Алдынғы бөлімде біз осы есептің дербес бір түрін атап айтқанда

,                                                    (2.5)

жағдайын  қарастырып, оның Коши есебінің бірі болатынына  көзімізді жеткіздік, енді басқа жағдайларды қарастырайық.

 ЖАҒДАЙЫ. Егер  болса,  онда келесі лемма орындалады 

ЛЕММА 2.1. Егер

1) ;  2) , болса, онда  (2)  шекаралық шарт мына түрге келтіріледі

,  ,                                               (2.6)

мұндағы - кез келген нөлден өзгеше комплекс сан.

ДӘЛЕЛІ. Мына  шартынан имеем ,    екенін көреміз, ал   теңдіктері мен  1.3 леммасынан

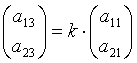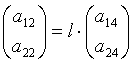,  ,  теңдіктері шығады. Демек шекаралық матрицаны түрі мына күйге енді

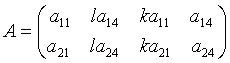.                                                           (2.7)

Онда   теңдігінен

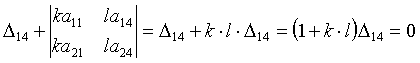,  демек, . Бұл теңдіктен   тұрақтыларының нөлден өзгеше екенін және олардың мына

.                                                                             (2.8)

формула  арқылы  байланысты екенін көреміз. Егерде (8)-ді (7)-ге апарып қойсақ, шекаралық матрица, мынадай,

.

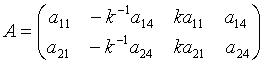болады, ал бұл матрицаға, мынадай,

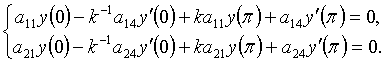
шекаралық шарт сай келеді. Мұны мынадай

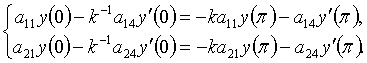
Система түрінде жазып, Крамердің тәсілі бойынша шешейік.

Қажетті анықтауыштарды есептейік, яғни  -лерді

;

;

.

;

.

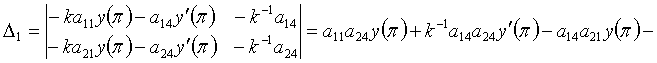
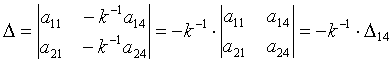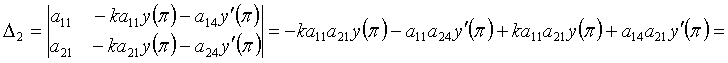
Алынған нәтижелерді жинақтап мына теорема түрінде тұжырымдайық.

ТЕОРЕМА 2.1. Егер  мына теңдіктер

,   орындалса, онда мынадай  -комплекс сан табылып, мына

,  .

теңдіктер орындалады

ҚОРЫТЫНДЫ

Шекаралық шарты мына

теңдікті қанағаттандыратын Штурм-Лиувиллдің болымсыз есебінің спектрәлдік қасиеттері теңдеудің коэффициентіне өте тәуелді екен.

Егер теңдеудің коэффициентіне мына

,

Шартты қанағаттандырса, онда оператор әсере болымсыз болады. Басқа жағдайда оператордың меншікті мәндері ендеулі жиын құрайды, олар осы есептің характеристикалық анықтауышының түбірлері болады. Бұл меншікті мәндердің асимтотикасын білу үшін  туралы қосымша мәліметтер керек.

                       ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1.  Марченко В.А. Операторы Штурма-Лиувилля и их приложения. – Киев: Наукова думка, 1998.-с.331.

2.  Титчмарш Е. Теория функции. – М.: Наука, 1999.-с.463.

3.  Леонтьев А.Ф. Целые функции. Ряды экспонент. – М.: Наука, 1983.-с.175.

4.  Винер Н., Пэли Р. Преобразования Фурье в комплексной плоскости. –   М.: Наука, 1964.-с.267.

5.  Наймарк М.А. Линейные дифференциальные операторы. – М.: Наука, 1969.-с.526.

6.  Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. - М.: ИЛ, 1958.-с.474.

7.  Ольвер Ф. Введение в асимптотические методы и специальные функции. – М.: Наука, 1978.-с.375.

8.  Треногин В.А. Функциональный анализ. – М.: Наука, 1980.-с.494.

9.  Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1-3. – М.: Наука, 1969.-с.607.

10. Мизохата С. Уравнения с частными производными. – М.: Мир, 1977.-с.504.

11. Кац Н.С. Кратность спектра дифференциального оператора второго порядка и разложении по собственным функциям //Изв. АН СССР 27 (1963), 1081-1112.

12. Штраус А.В. О кратности спектра самосопряженного обыкновенного дифференциального оператора // ДАН СССР 155, 4 (1964), 771-774.

13. Левитан Б.М. Введение в спектральную теорию операторов.- М.: Наука, 1968.