![]() (1.13)
(1.13)
является корреляционным эллипсоидом случайного вектора
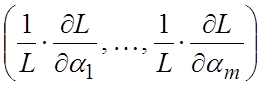 . (1.14)
. (1.14)
Теперь
рассмотрим набор несмещенных оценок (1.11) и составим вектор
случайных уклонений ![]() с нулевым вектором
средних и корреляционной матрицей
с нулевым вектором
средних и корреляционной матрицей
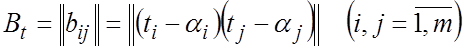 . (1.15)
. (1.15)
Если сформировать теперь квадратичную форму ![]() при любом векторе
при любом векторе ![]() , то имеет место следующая
теорема.
, то имеет место следующая
теорема.
Теорема Рао-Крамера. При
условии существования неособенной информационной матрицы Фишера I (1.12)
и величин 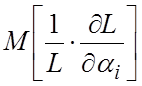 , при любом
, при любом
![]() имеет место неравенство:
имеет место неравенство:
![]() , (1.16)
, (1.16)
где Bt – корреляционная матрица (1.15) вектора оценок (1.11).
Если
теперь вектор Z такой, что ![]() , то из (1.16) следует, что корреляционный эллипсоид
, то из (1.16) следует, что корреляционный эллипсоид ![]() охватывает корреляционный эллипсоид
охватывает корреляционный эллипсоид ![]() . Т.е. с помощью любых статистик t нельзя
получить более точных оценок
. Т.е. с помощью любых статистик t нельзя
получить более точных оценок ![]() , чем в случае, когда эти два эллипсоида совпадают.
, чем в случае, когда эти два эллипсоида совпадают.
Статистики
ti, дающие несмещенные оценки параметрам ai ![]() , для которых эллипсоид
, для которых эллипсоид ![]() совпадает с эллипсоидом
совпадает с эллипсоидом ![]() , называется совместно эффективными оценками параметров
, называется совместно эффективными оценками параметров ![]() .
.
11.5. Методы оценивания.
Основными
способами оценивания параметров в математической статистике являются: метод максимального правдоподобия и метод
моментов. Метод моментов введен К. Пирсоном. Пусть имеется повторная выборка ![]() с функцией правдоподобия
с функцией правдоподобия
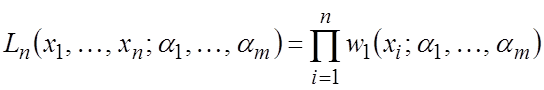
Составляет m выборочных моментов
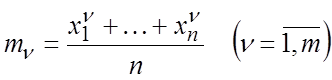 .
.
При ![]()
![]() ,
,
т.е. с ростом объема выборки оценки mn становятся состоятельными.
Метод
максимального правдоподобия разработан Д. Бернулли,
Ф. Гауссом и К.Р. Фишером.
При этом способе за оценки ![]() выбираются
такие значения параметров, которые дают максимальное значение функции
правдоподобия, если их подставить на место
выбираются
такие значения параметров, которые дают максимальное значение функции
правдоподобия, если их подставить на место
![]() .
Если
.
Если ![]() для повторной выборки дифференцируема, то пользуясь однозначностью
логарифмической функции, удобнее искать максимум не самой функции
правдоподобия, а ее логарифма. В этом случае уравнения правдоподобия
примут вид
для повторной выборки дифференцируема, то пользуясь однозначностью
логарифмической функции, удобнее искать максимум не самой функции
правдоподобия, а ее логарифма. В этом случае уравнения правдоподобия
примут вид
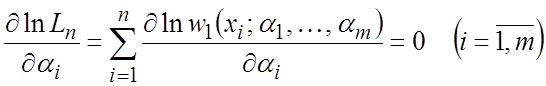 . (1.17)
. (1.17)
Оценки,
получаемые из уравнения (1.17) называются оценками максимального
правдоподобия. Они обозначаются 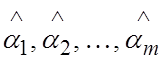 и
имеют ряд
замечательных свойств. Данные оценки асимптотически несмещенные, асимптотически
эффективные и асимптотически нормальные. Как
правило, уравнения (1.17) имеют единственное
решение.
и
имеют ряд
замечательных свойств. Данные оценки асимптотически несмещенные, асимптотически
эффективные и асимптотически нормальные. Как
правило, уравнения (1.17) имеют единственное
решение.
Пример. Оценки ![]() и s2 параметров
a и s 2 нормального
распределения
и s2 параметров
a и s 2 нормального
распределения ![]() по выборке xi
по выборке xi ![]() являются оценками максимального правдоподобия,
т.е. они получены из решения системы (1.17), записанной для
функции правдоподобия
являются оценками максимального правдоподобия,
т.е. они получены из решения системы (1.17), записанной для
функции правдоподобия ![]() из рассматриваемых в данной главе примеров.
из рассматриваемых в данной главе примеров.
Как известно, измерение является процессом получения информации о свойствах физических объектов, поэтому с помощью измерений решаются самые разнообразные физические задачи, требующие применения широкого спектра методов обработки результатов измерений.
Так как все измерения сопровождаются случайными погрешностями, то обработка результатов измерений всегда включает в себя операции над случайными величинами или процессами, в основе которых лежат методы теории вероятностей и математической статистики.
Поскольку результаты измерений являются случайными величинами, то с их помощью невозможно получить истинные значения измеряемых параметров. Речь может идти только о нахождении некоторых оценок данных параметров, которые сами тоже будут являться случайными величинами.
Чтобы
оценка ![]() некоторой измеряемой величины
некоторой измеряемой величины ![]() была в определенном смысле
"хорошей", она должна удовлетворять следующим критериям [1, 2]:
оценка должна быть состоятельной, несмещенной и эффективной.
была в определенном смысле
"хорошей", она должна удовлетворять следующим критериям [1, 2]:
оценка должна быть состоятельной, несмещенной и эффективной.
Оценка
называется состоятельной, если при увеличении числа опытов ![]() оценка
оценка ![]() приближается
к истинному значению
приближается
к истинному значению ![]() . Оценка называется
несмещенной, если ее математическое ожидание равно истинному значению
. Оценка называется
несмещенной, если ее математическое ожидание равно истинному значению ![]() , т.е.
, т.е. ![]() .
Несмещенная оценка не содержит систематической погрешности. Оценка называется
эффективной, если по сравнению с другими она обладает наименьшей дисперсией,
т.е.
.
Несмещенная оценка не содержит систематической погрешности. Оценка называется
эффективной, если по сравнению с другими она обладает наименьшей дисперсией,
т.е. ![]() .
.
Получение "хороших" оценок требует определения критерия их сравнения. Если таковой установлен, то наилучшей оценкой будет та, которая обеспечит экстремум этого критерия. На практике наибольшее распространение получил метод максимального правдоподобия (ММП).
В ММП в качестве критерия оптимальности оценок используется функция правдоподобия, представляющая собой плотность вероятности всей совокупности экспериментальных данных. Искомые оценки находятся из условия максимума функции правдоподобия, что фактически соответствует максимуму вероятности получения именно тех результатов измерения, которые были получены в опытах.. Вычисление функции правдоподобия требует знания вида закона распределения погрешностей измерений. В случае, когда погрешности имеют нормальный закон распределения, ММП сводится к методу наименьших квадратов (МНК), в котором в качестве критерия сравнения оценок используется сумма квадратов отклонений результатов измерений от полученной оценки измеряемой величины (или функции).
Наряду с получением оценки искомой величины в виде одного числа (точечное оценивание) широкое распространение получило оценивание с помощью доверительных интервалов.
Доверительным интервалом называется интервал значений оцениваемой величины, который с заданной вероятностью (доверительной вероятностью) накрывает истинное значение этой величины. Доверительный интервал является случайным интервалом: случайны его положение и длина, вычисляемые, как правило, по опытным данным.
Пусть
истинное значение измеряемой величины равно c (оно неизвестно), и проведено
![]() аналогичных измерений, результаты которых равны
аналогичных измерений, результаты которых равны ![]() . Данную последовательность из
. Данную последовательность из ![]() величин называют выборкой, элементы
которой равны:
величин называют выборкой, элементы
которой равны:
![]()
![]() , (1)
, (1)
где ![]() – погрешность наблюдений в
– погрешность наблюдений в
![]() -м измерении. По результатам
наблюдений
-м измерении. По результатам
наблюдений ![]() необходимо найти
необходимо найти ![]() оценку неизвестного параметра
оценку неизвестного параметра ![]() .
.
Относительно
погрешностей ![]() сделаем следующие предположения:
сделаем следующие предположения:
1)
погрешность ![]() является случайной величиной с
нормальным законом распределения, символически это можно записать
является случайной величиной с
нормальным законом распределения, символически это можно записать 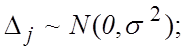
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.